Scalar Triple Product of Vectors

The Scalar Triple Product means the product of three vectors which result in a scalar number. It means taking the dot product of the vectors with the cross product of the other two vectors. In real life, we use Scalar Triple Product to solve complex problems related to aircraft design and structural analysis.

This Story also Contains

1. Scalar Triple Product: Definition
2. Geometrical interpretation
3. Volume of Tetrahedron
4. Properties of Scalar Triple Product
5. Solved Examples Based on Scalar Triple Product of Vectors

In this article, we will cover the concept of Scalar Triple Product. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of twenty-six questions have been asked on this topic in JEE Main from 2013 to 2023 including two in 2019, three in 2020, six in 2021, two in 2022, and eleven in 2023.

Scalar Triple Product: Definition

The scalar triple product (also called the mixed or box product) is defined as the dot product of one of the vectors with the cross product of the other two.

If $\vec{a}, \vec{b}$ and $\vec{c}$ are any three vectors, then their scalar product is defined as $\overrightarrow{\mathbf{a}} \cdot(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}})$ and it is denoted as $[\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}}]$.
Scalar Triple Product: Formula
The scalar triple product can be evaluated numerically using any one of the following

$
\begin{array}{ll}
& (\vec{a} \times \vec{b}) \cdot \vec{c}=\overrightarrow{\mathbf{a}} \cdot(\vec{b} \times \overrightarrow{\mathbf{c}})=\overrightarrow{\mathbf{b}} \cdot(\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{a}})=\overrightarrow{\mathbf{c}} \cdot(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \\
\text { i.e. } \quad & {\left[\begin{array}{lll}
\overrightarrow{\mathbf{a}} & \vec{b} & \overrightarrow{\mathbf{c}}
\end{array}\right]=\left[\begin{array}{lll}
\vec{b} & \overrightarrow{\mathbf{c}} & \overrightarrow{\mathbf{a}}
\end{array}\right]=\left[\begin{array}{lll}
\overrightarrow{\mathbf{c}} & \overrightarrow{\mathbf{a}} & \vec{b}
\end{array}\right]=-\left[\begin{array}{lll}
\vec{b} & \overrightarrow{\mathbf{a}} & \overrightarrow{\mathbf{c}}
\end{array}\right]=-\left[\begin{array}{lll}
\overrightarrow{\mathbf{c}} & \vec{b} & \overrightarrow{\mathbf{a}}
\end{array}\right]}
\end{array}
$

The parentheses may be omitted without causing ambiguity since the dot product cannot be evaluated first. If it were, it would leave the cross product of a scalar and a vector, which is not defined.

Scalar Triple Product Proof

If $\overrightarrow{\mathbf{a}}=a_1 \hat{\mathbf{i}}+a_2 \hat{\mathbf{j}}+a_3 \hat{\mathbf{k}}, \overrightarrow{\mathbf{b}}=b_1 \hat{\mathbf{i}}+b_2 \hat{\mathbf{j}}+b_3 \hat{\mathbf{k}}$ and $\overrightarrow{\mathbf{c}}=c_1 \hat{\mathbf{i}}+c_2 \hat{\mathbf{j}}+c_3 \hat{\mathbf{k}}$ then

$
\begin{aligned}
{\left[\begin{array}{lll}
\overrightarrow{\mathbf{a}} & \overrightarrow{\mathbf{b}} & \overrightarrow{\mathbf{c}}
\end{array}\right] } & =(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}) \cdot \overrightarrow{\mathbf{c}}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
a_1 & a_2 & a_2 \\
b_1 & b_2 & b_3
\end{array}\right| \cdot\left(c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}\right) \\
& =\left|\begin{array}{ccc}
\hat{i} \cdot\left(c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}\right) & \hat{j} \cdot\left(c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}\right) & \hat{k} \cdot\left(c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}\right) \\
a_1 & a_2 & a_2 \\
b_1 & b_2 & b_3
\end{array}\right|
\end{aligned}
$

NOTE :

1. $\left[\begin{array}{lll}m \vec{a} & \vec{b} & \vec{c}\end{array}\right]=m\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]$, where $m$ is a scalar..
2. $\left[\begin{array}{llll}m_1 \vec{a} & m_2 & \vec{b} & m_3 \vec{c}\end{array}\right]=m_1 m_2 m_3\left[\begin{array}{lll}\vec{a} & \vec{b} & \vec{c}\end{array}\right]$, where $m_1, m_2, m_3$ are scalares.
3. $\quad\left[\begin{array}{llll}\vec{a}+\vec{b} & \vec{c} & \vec{d}\end{array}\right]=\left[\begin{array}{lll}\vec{a} & \vec{c} & \vec{d}\end{array}\right]+\left[\begin{array}{lll}\vec{b} & \vec{c} & \vec{d}\end{array}\right]$

The necessary and sufficient condition for three non-zero, non-collinear vectors $\vec{a}, \vec{b}$ and $\vec{c}$ is coplanar is that $\left[\begin{array}{lll}\vec{a} & b & \vec{c}\end{array}\right]=0$

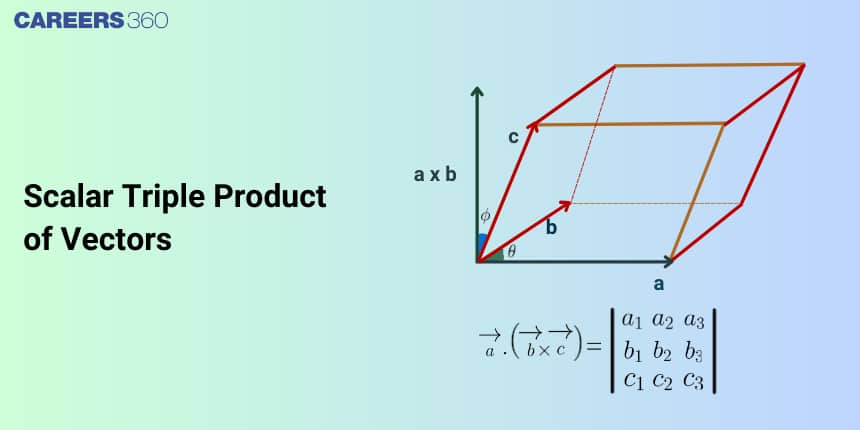
Geometrical interpretation

Let vectors $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ represent the sides of a parallelepiped $O A, O B$ and OC respectively. Then, $\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}$ is a vector perpendicular to the plane of $\overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$. Let $\theta$ be the angle between vectors $\overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ and $\alpha$ be the angle between $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}$. If $\hat{\mathbf{n}}$ is a unit vector along $\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}$, then $\alpha$ is the angle between $\hat{\mathbf{n}}$ and $\overrightarrow{\mathbf{a}}$.

$\begin{aligned} {[\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}}] } & =\overrightarrow{\mathbf{a}} \cdot(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}) \\ & =\overrightarrow{\mathbf{a}} \cdot(\mathbf{b} \mathbf{c} \sin \theta \hat{\mathbf{n}}) \\ & =(\mathbf{b} \mathbf{s} \sin \theta)(\overrightarrow{\mathbf{a}} \cdot \hat{\mathbf{n}}) \\ & =(\mathbf{b} \mathbf{s} \sin \theta)(\mathbf{a} \cdot \mathbf{1} \cdot \cos \alpha) \\ & =(\mathbf{a} \cdot \cos \alpha)(\mathbf{b} \mathbf{c} \sin \theta) \\ & =\text { (Height) } \cdot \text { (Area of Base) } \\ & =\text { Volume of parallelepiped }\end{aligned}$

Volume of Tetrahedron

A tetrahedron is a pyramid having a triangular base. Therefore

$
\therefore \quad \text { Volume }=\frac{1}{6}\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]
$

Properties of Scalar Triple Product

If $\vec{a}, \vec{b}$ and $\vec{c}$ are vectors
1) $(\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}), \vec{c}=\overrightarrow{\mathbf{a}} \cdot(\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}})$ i.e. position of the dot and the cross can be interchanged without altering the product.
2) $\vec{a}, \vec{b}$ and $\vec{c}$ in that order form a right-handed system if $[\vec{a} \vec{b} \quad \vec{c}]_{>0}$;
$\vec{a}, \vec{b}$ and $\vec{c}$ in that order form a lett-handed system if $[\overrightarrow{\mathbf{a}} \overrightarrow{\mathbf{b}} \overrightarrow{\mathbf{c}}]<0$
3) $[\vec{a} \vec{a} \vec{b}]=0(\vec{a}$ is perpendicular to ( $\vec{a} \times \vec{b}), \vec{a} \cdot(\vec{a} \times \vec{b})=0)$

Recommended Video Based on Scalar Triple Product of Vectors

Solved Examples Based on Scalar Triple Product of Vectors

Example 1: Let $\vec{a}$ and $\vec{b}$ be two vectors, Let $|\vec{a}|=1,|\vec{b}|=4$ and $\vec{a} \cdot \vec{b}=2$. If $\vec{c}=(2 \vec{a} \times \vec{b})-3 \vec{b}$, then the value of $\vec{b} \cdot \vec{c}$ is
[JEE MAINS 2023]
Solution: $\vec{b} \cdot \vec{c}=(2 \vec{a} \times \vec{b}) \cdot \vec{b}-3 \vec{b} \cdot \vec{b}$
$=0-3 b^2$
$=-3 \times 16=-48$
$\vec{b} \cdot \vec{c}=-48$
Hence, the answer is -48
Example 2: If four distinct points with position vectors $\vec{a}, \vec{b}, \vec{c}$ and $d$ are coplanar, then $[\vec{a} \vec{b} \vec{c}]$ is equal to
[JEE MAINS 2023]
Solution: $\vec{a}, \vec{b}, \vec{c}, \vec{d} \rightarrow$ coplanar
$[\overrightarrow{\mathrm{a}} \overrightarrow{\mathrm{b}} \overrightarrow{\mathrm{c}}]=$ ?
$\vec{b}-\vec{a}, \vec{c}-\vec{b}, \vec{d}-\vec{c} \rightarrow$ coplanar
$[\vec{b}-\vec{a} \vec{c}-\vec{b}, \vec{d}-\vec{c}]=0$
$\Rightarrow(\vec{b}-\vec{a}) \cdot((\vec{c}-\vec{b}) \times(\vec{d}-\vec{c}))=0$
$(\vec{b}-\vec{a}) \cdot(\vec{c} \times \vec{b}-\vec{c} \times \vec{a}-\vec{a} \times \vec{d})=0$
$[\mathrm{bcd}]-[\mathrm{bca}]-[\mathrm{bad}]-[\mathrm{acc} d]=0$
$[\vec{a} \vec{b} \vec{c}]=[\vec{d} \vec{c} \vec{a}]+[\vec{b} \vec{d} \vec{a}]+[\vec{c} \vec{d} \vec{b}]$
Hence, the answer is $[\vec{d} \vec{c} \vec{a}]+[\vec{b} \vec{d} \vec{a}]+[\vec{c} \vec{d} \vec{b}]$

Example 3 : Let $\vec{v}=\alpha \hat{\imath}+2 \hat{j}-3 \hat{k}, \vec{w}=2 \alpha \hat{\imath}+\hat{\jmath}-\hat{k}$ and $\vec{u}$ be a vector such that $|\vec{u}|=\alpha>0$. If the minimum value of the scalar triple product $[\vec{u} \vec{v} \vec{w}]$ is $-\alpha \sqrt{3401}$, and $|\vec{u} \cdot \hat{\imath}|^2=\frac{m}{n}$ where $m$ and $n$ are coprime natural numbers, then $m+n_{\text {is equal to }}$
[JEE MAINS 2023]
Solution

$
\begin{aligned}
& \Rightarrow-\alpha \sqrt{1+34 \alpha^2}=-\alpha \sqrt{3401} \\
& \Rightarrow \alpha^2=100 \\
& \Rightarrow \alpha=10
\end{aligned}
$

$\overrightarrow{\mathrm{u}}$ is parallel to $\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{w}} \quad\{\because \alpha>0\}$

$
\begin{aligned}
& \overrightarrow{\mathrm{u}}=\lambda(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{w}}) \\
& \overrightarrow{\mathrm{u}}=\lambda(\hat{\mathrm{i}}-50 \hat{j}-30 \hat{k})
\end{aligned}
$
$
\begin{aligned}
& |\overrightarrow{\mathrm{u}}|=10 \\
& |\lambda| \sqrt{3401}=10 \\
& |\lambda|=\frac{10}{\sqrt{3401}} \quad \overrightarrow{\mathrm{u}}= \pm \frac{10}{\sqrt{3401}}(\hat{\mathrm{i}}-50 \hat{\mathrm{j}}-30 \hat{\mathrm{k}}) \\
& \left|\overrightarrow{\mathrm{u}} \cdot \hat{\left.\right|^2}\right|^2=\frac{100}{3401}=\frac{\mathrm{m}}{\mathrm{n}} \\
& \mathrm{m}+\mathrm{n}=100+3401=3501
\end{aligned}
$
Hence, the answer is 3501 .

Example 4: If $\vec{a}=2 \hat{i}+\hat{j}+3 \hat{k}, \quad \vec{b}=3 \hat{i}+3 \hat{j}+\hat{k}$ and $\vec{c}=c_1 \hat{i}+c_2 \hat{j}+c_3 \hat{k}$ are coplanar vectors and $\vec{a} \cdot \vec{c}=5, \vec{b} \perp \vec{c}$, then $122\left(c_1+c_2+c_3\right)$ is equal to $\qquad$
[JEE MAINS 2022]

$
\begin{aligned}
& \text { Solution: } \vec{a} \cdot \vec{c}=5 \Rightarrow 2 C_1+C_2+3 C_3=5 \cdots(1) \\
& \vec{b} \perp \vec{c}=3 C_1+3 C_2+C_3=0 \cdots(2) \\
& \begin{aligned}
\vec{a}, \vec{b}, \vec{c} \text { are coplanaı } \Rightarrow & \left|\begin{array}{ccc}
C_1 & C_2 & C_3 \\
2 & 1 & 3 \\
3 & 3 & 1
\end{array}\right|=0 \\
& \Rightarrow-8 \mathrm{C}_1+7 \mathrm{C}_2+3 \mathrm{C}_3=0 \cdots-(3)
\end{aligned}
\end{aligned}
$
$
\begin{aligned}
& \text { Eliminating } \mathrm{C}_3 \text { from (1) \& (3) } \Rightarrow \begin{aligned}
& 10 \mathrm{C}_1-6 \mathrm{C}_1=5---(4) \\
& \text { from (2) \& (3) } \Rightarrow 17 \mathrm{C}_1+2 \mathrm{C}_2=0---(5) \\
& \Rightarrow 51 \mathrm{C}_1+6 \mathrm{C}_2=0---(6) \\
& \Rightarrow 61 \mathrm{C}_1=5 \Rightarrow \mathrm{C}_1=\frac{5}{61}, \mathrm{C}_2=\frac{-1}{2} \times 17 \mathrm{C}_1=\frac{-85}{122} \\
& \mathrm{C}_3=-3\left(\mathrm{C}_1+\mathrm{C}_2\right)
\end{aligned}
\end{aligned}
$
So $C_1+C_2+C_3=-2\left(C_1+C_2\right)=\left(\frac{85}{61}-\frac{10}{61}\right)$

$
\Rightarrow 122\left(\mathrm{C}_1+\mathrm{C}_2+\mathrm{C}_3\right)=75 \times 2=150
$
Hence, the answer is 150 .

Example 5: Let the volume of a parallelopiped whose coterminous edges are given by $\vec{u}=\widehat{i}+\widehat{j}+\lambda \widehat{k}, \vec{v}=\widehat{i}+\widehat{j}+3 \widehat{k}$ and $\vec{w}=2 \widehat{i}+\widehat{j}+\widehat{k}$ be 1 cu. unit. If $\theta$ be the angle between the edges $\vec{u}$ and $\vec{w}$,then cos $\theta$ can be :
Solution: Volume of parallelopiped $=1$

$
\pm 1=\left|\begin{array}{lll}
1 & 1 & \lambda \\
1 & 1 & 3 \\
2 & 1 & 1
\end{array}\right| \Rightarrow=-\lambda+3= \pm 1 \Rightarrow \lambda=2 \text { or } \lambda=4
$
For $\lambda=4 \frac{1}{90}$

$
\cos \theta=\frac{2+1+4}{\sqrt{6} \sqrt{18}}=\frac{7}{6 \sqrt{3}}
$
Hence, the answer is $\frac{7}{6 \sqrt{3}}$