Power set

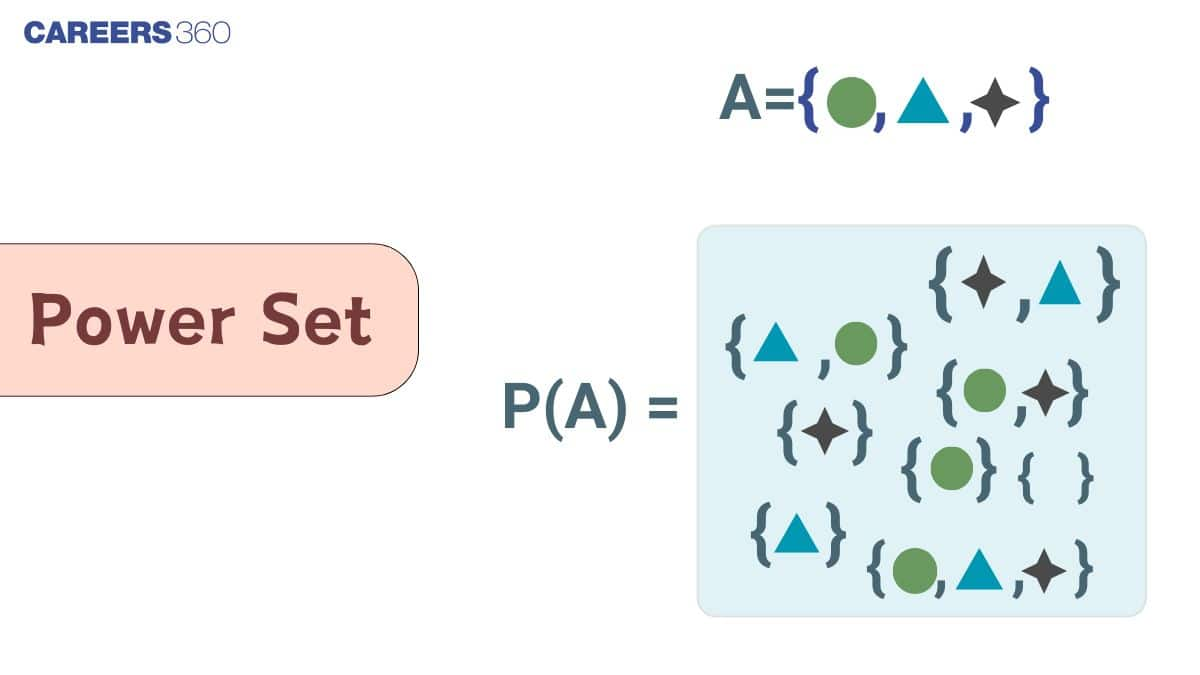
What is a Power Set?

The set of all subsets of a set $S$ is called the power set of$S$. It is denoted by $P(S)$. It also includes the empty set and the set itself. The power set always contains $2^n$ elements, where $n$ is the number of elements in the original set.

Power Set Definition: The collection of all subsets of a set $A$ is called the power set of $A$. It is denoted by $P(A)$.

Power Set Example: Let $\mathrm{A}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$, then $P(A)=\{\phi,\{a\},\{b\},\{c\},\{a, b\},\{b, c\},\{c, a\},\{a, b, c\}\}$

Cardinality of Power Set

The number of distinct elements in a finite set $A$ is called the Cardinal number or cardinality of set and it is denoted by $A$ and it is denoted by $n(A)$.

The power set formula to find the cardinality(number of elements) of the power set of any set $A$ is $2^n$ where $n$ is the number of elements in $A$.

Eg. Let $\mathrm{A}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$. The cardinality of the set $A$ is $3$. The cardinality of the power set of $A$, $P(A)$ is $2^n = 2^3 = 8$.

Properties of Power Set

The properties of the power set are :

• The power set of any set is non-empty.
• Each element of a Power set is a set.
• Number of elements in $P(A)=$ Number of subsets of $\operatorname{set} A =2 ^{n(A)}$ where $n(A)$ is the number of elements in set $A$
• It is always larger than the original set.
• The power set of a finite set has a finite number of elements.
• For a set of natural numbers, we can do a one-to-one mapping of the resulting set, $P(S)$, with the real numbers.
• $P(S)$ of set $S$, if operated with the union of sets, the intersection of sets and the complement of sets, denotes the example of Boolean Algebra.

Power Set Examples with Solutions

Working through examples is one of the best ways to understand the concept of a power set. By listing all possible subsets of different sets, we can clearly see how power sets are formed and how their size follows the $2^n$ rule. This section provides step-by-step power set examples with detailed solutions for better clarity.

Power Set of 2-Element Set

Let the original set be $A = \{1, 2\}$.

To find the power set of a 2-element set, we list all possible subsets of $A$, including the empty set and the set itself.

The subsets of $A$ are:

• $\emptyset$
• $\{1\}$
• $\{2\}$
• $\{1, 2\}$

Hence, the power set of $A$ is:

$P(A) = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\}$

The total number of subsets = $2^n = 2^2 = 4$

Power Set of 3-Element Set

Let $B = \{a, b, c\}$
To find the power set of a 3-element set, we again list all possible combinations of elements.

The subsets of $B$ are:

• $\emptyset$
• $\{a\}, \{b\}, \{c\}$
• $\{a, b\}, \{a, c\}, \{b, c\}$
• $\{a, b, c\}$

So, the power set of $B$ is:

$P(B) = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}$

Total subsets = $2^3 = 8$

Verifying Total Subsets Using $2^n$

The number of elements in a power set is given by the formula:

$|P(S)| = 2^n$

where $n$ is the number of elements in the original set $S$.
For example, if $S = \{x, y, z, w\}$, then $n = 4$ and:

$|P(S)| = 2^4 = 16$

This formula helps verify whether all subsets have been correctly listed when creating a power set.

Power Set in Mathematics and Real-Life Applications

The concept of a power set extends beyond theoretical math and finds applications in various real-life and academic fields. From logic and programming to probability and combinatorics, power sets help model choices, events, and states. This section explores how power sets are used in both mathematics and practical scenarios.

Power Set in Boolean Algebra and Logic

In Boolean algebra, the power set is often used to represent truth tables and logical operations. Each subset in the power set can correspond to a specific combination of truth values.
For instance, for a set $S = \{p, q\}$ representing propositions, its power set models all possible truth value assignments to $p$ and $q$. This is crucial in designing logical circuits and truth tables.

Use of Power Set in Computer Science and Programming

In computer science, the concept of a power set is essential in various algorithms:

• Generating all possible combinations in recursive or iterative programming
• Bitmasking techniques, where each bit representsthe inclusion/exclusion of an element
  For a set with $n$ elements, the power set helps in solving problems involving subset generation, permissions systems, and state spaces.

Power Set in Combinatorics and Probability

In combinatorics, the power set represents the complete collection of subsets, allowing us to count or evaluate combinations.
In probability, if each subset represents a possible event, the power set forms the sample space of all possible events.
For example, if $A = \{\text{Rain}, \text{Snow}\}$, the power set gives us:

$P(A) = \{\emptyset, \{\text{Rain}\}, \{\text{Snow}\}, \{\text{Rain, Snow}\}\}$

Each element of $P(A)$ represents a possible outcome or event in the probability space.

Difference Between Set and Power Set

Understanding the difference between a set and its power set is crucial in set theory. While a set contains individual elements, its power set includes all possible subsets of those elements. This section explains how the two differ in structure, size, and representation.

Element vs Subset

A set contains individual elements, while a power set contains subsets of those elements.
For example:

• Set: $S = {1, 2}$
• Power set: $P(S) = \{\emptyset, {1}, {2}, {1, 2}\}$

In $S$, $1$ is an element. In $P(S)$, $\{1\}$ is a subset.
This highlights the difference between elements and subsets in power sets.

Cardinality Comparison

Let $T$ be a finite set with $n$ elements.

• Cardinality of the set: $|T| = n$
• Cardinality of the power set: $|P(T)| = 2^n$

Example:
If $T = \{a, b, c\}$, then:

• $|T| = 3$
• $|P(T)| = 2^3 = 8$

The power set always has exponentially more elements than the original set. This cardinality difference between a set and its power set is a key concept in set theory and combinatorics.

Solved Examples Based on Power Set

Example 1: Power set of $\{1,2,3\}$ is
1) $P(A)=\{\phi,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\}\}$
2) $P(A)=\{\{1\},\{2\},\{3\},\{1,2\},\{1,3\}\{2,3\},\{1,2,3\}\}$
3) $P(A)=\{\phi,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}$
4) None of the above

Solution:
As we know, in this question,
Option (3) shows all the subsets of $\{1,2,3\}$
Hence, the answer is option 3.

Example 2: Find the number of elements in the power set of $\{1,2,3,4,5\}$.
1) $8$
2) $16$
3) $32$
4) $64$

Solution:
As we know, in this question,
The power set of $\{1,2,3,4,5\}$ will have $2^5=32$ elements.
Hence, the answer is option 3.

Example 3: $\mathbf{A}$ is a set containing $\mathbf{n}$ elements. A subset $P_1$ is chosen and $\mathbf{A}$ is reconstructed by replacing the elements of $P_1$. The same process is repeated for subsets $P_1, P_2, \ldots, P_m$ with $m>1$. The number of ways of choosing $P_1, P_2, \ldots, P_m$, $P_1 \cup P_2 \cup \ldots \cup P_m=A$ so that $P_1 \cup P_2 \cup \ldots \cup P_m=A$ is
1) $\left(2^m-1\right)^{m n}$
2) $\left(2^n-1\right)^m$
3) ${ }^{m+n} C_m$
4) none of these

Solution:
$\operatorname{Let} A=\left\{a_1, a_2, \ldots, a_n\right\}$ for each $a_i(1 \leq i \leq n)$
Either $a_i \in P_j$ or $a_i \notin P_j(1 \leq j \leq m)$
$\therefore$ There are $2^m$ choices in which $a_i, a_j$ belongs to $P_j$,
Also, there is exactly one choice, i.e, $a_i \notin P_j$
$\therefore a_i \in P_1 \cup P_2 \cup \ldots \cup P_m$ in ( $2^m-1$ ) ways.
Since there are n elements in the set A, the number of ways of constructing subsets.
$P_1, P_2, \ldots, P_m$ is $\left(2^m-1\right)^n$

Example 4: The number of elements in the power set of $P(P(\phi))$ is
1) $1$
2) $2$
3) $3$
4) $4$

Solution:
Number of elements in $\mathrm{P}(\phi)$ is $2^0=1$
Number of elements in $\mathrm{P}(\mathrm{P}(\phi))$ is $2^1=2$
Hence, the answer is option 2.

Example 5: A relation on the set $A=\{x:|x|<3, x \in Z\} \quad$ where $\mathbf{Z}$ is the set of integers is defined by $R=\{(x, y): y=|x|, x \neq-1\}$ Then the number of elements in the power set of $\mathbf{R}$ is :
1) 32
2) 16
3) 8
4) 64

Solution:
Consider set $A=\{x:|x|<3, x \in Z\}$.
All elements of the set A, defined by x, are also contained in Z, the set of integers. It's also given that the absolute value of these elements is strictly less than 3.
$|x|<3 \Rightarrow|x| \in\{0,1,2\} \subset A$
Hence, possibly this set in roster form will be,
$A=\{-2,-1,0,1,2\}$
A relation R on the set A where $R \subseteq(A \times A)$ is defined in set builder notation as
$R=\{(x, y): y=|x|, x \neq-1\}$
Thus, $ xRy$ is possible if y is the absolute value of x and x is not equal to -1.
And also, $(x, y) \in(A \times A)$
$|x|=y \in\{0,1,2\}$
$\therefore x \in\{-2,0,1,2\} \quad \text { but } \quad x \neq-1$
Hence, possibly $R$ in roster form will be,
$R=\{(-2,2),(0,0),(1,1),(2,2)\}$
Here we get that $|R|=4$.
Thus,
$|P(R)|=2^{|R|}=2^4=16$
Hence, the answer is option 2.

List of Topics Related to Power Set

To fully grasp the concept of a power set, it is essential to understand the foundational topics of set theory that support it. These related concepts, such as union, intersection, complement, and set representation, form the basis for generating and analysing power sets. In this section, we highlight all the key topics that are directly or indirectly connected to the idea of power sets.

NCERT Resources

Explore essential NCERT study materials for Sets, with comprehensive solutions, concise revision notes, and curated exemplar problems. These resources are designed to enhance your conceptual clarity and prepare effectively for board and competitive exams.

NCERT Solutions for Class 11 Chapter 1 Sets

NCERT Notes for Class 11 Chapter 1 Sets

NCERT Exemplar for Class 11 Chapter 1 Sets

Practice Questions on Power Sets

Mastering any mathematical concept comes through continuous practice. To help strengthen your understanding of the topic, we have provided some practice questions on Power Set. They will test your knowledge of formulas, important properties and general application of knowledge.

To practice questions based on Power Set Universal Set - Practice Question MCQ click here.

You can practice the next topics of Sets below: