Left-Hand and Right-Hand Limits: Definition, Formula, Examples

What Are Left-Hand and Right-Hand Limits?

We often want to know how a function behaves as it gets close to a specific point. Left-hand limits and right-hand limits let us examine this behavior from different directions. Imagine walking toward a doorway from the left versus the right—the view might look different depending on your approach.

Understanding One-Sided Limits

A one-sided limit is the value that a function approaches as $x$ gets closer to a point from only one side.

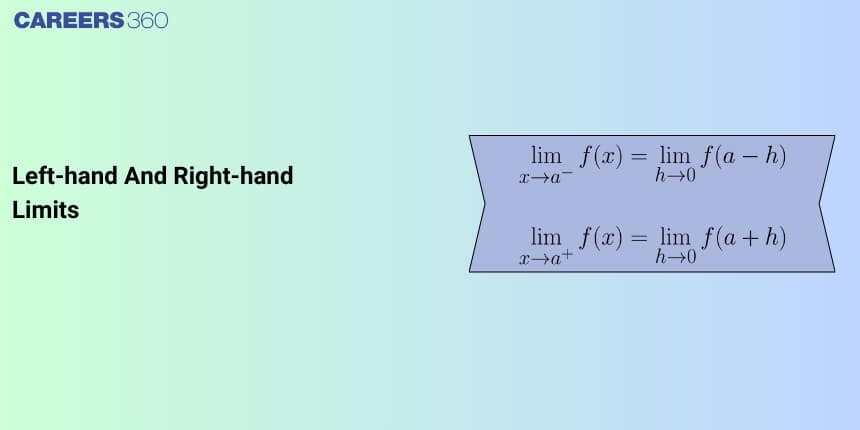
The left-hand limit (LHL) considers $x$ approaching from smaller values and is written as $\lim_{x \to a^-} f(x)$.

The right-hand limit (RHL) considers $x$ approaching from larger values and is written as $\lim_{x \to a^+} f(x)$.

One-sided limits are very useful for piecewise functions or functions with discontinuities, helping us see how the function behaves near a point.

Difference Between Left-Hand Limit (LHL) and Right-Hand Limit (RHL)

The LHL is the value $f(x)$ approaches as $x \to a$ from the left.

The RHL is the value $f(x)$ approaches as $x \to a$ from the right.

For the limit of $f(x)$ at $x = a$ to exist, we must have:
$\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x)$

If these are not equal, the function has a discontinuity at that point.

Understanding the difference between LHL and RHL is essential for calculating limits, analyzing graphs, and solving real-world problems using one-sided limits.

Now, let us observe the values of $f(x)$ nearby $x=7$.

$\lim\limits _{x \rightarrow 7^{-}} f(x)=8$

Approaching a Point from the Left

Approaching $7$ from the left means the values of $x$ are just less than $7$.

If for such values of $x$, $f(x)$ is close to $L$, then $L$ is called the left-hand limit of the function at $x=7$.

For example, for this function, $8$ is the left-hand limit of $f(x)$ at $x=7$.

We denote it as: $\lim_{x \to 7^-} f(x) = 8$
Here, $7^-$ indicates values less than $7$ but infinitesimally close to $7$.

Approaching a Point from the Right

Approaching $7$ from the right means the values of $x$ are just greater than $7$.

If for such values of $x$, $f(x)$ is close to $R$, then $R$ is called the right-hand limit of the function at $x=7$.

For this function, $8$ is the right-hand limit of $f(x)$ at $x=7$.

We denote it as:
$\lim_{x \to 7^+} f(x) = 8$
Here, $7^+$ indicates values greater than $7$ but infinitesimally close to $7$.

When LHL Equals RHL

In this example, the left-hand limit and right-hand limit are the same.

This means we can define the value of the function at $x=7$ as $f(7)=8$.

In general:

• The left-hand limit of $f(x)$ as $x$ approaches $a$ is:
  $\lim_{x \to a^-} f(x) = LHL$

• The right-hand limit of $f(x)$ as $x$ approaches $a$ is:
  $\lim_{x \to a^+} f(x) = RHL$

Example: Function $f(x) = \frac{|x|}{x}$

Let’s check the behavior of $f(x)$ near $x=0$.

Left-hand limit:
$\mathrm{LHL} = \lim_{x \to 0^-} \frac{|x|}{x}$
Since $x$ is just less than $0$, we write $x = 0-h$, where $h>0$ and very small:
$\lim_{h \to 0^+} \frac{| -h |}{-h} = \lim_{h \to 0^+} \frac{h}{-h} = -1$

Right-hand limit:
$\mathrm{RHL} = \lim_{x \to 0^+} \frac{|x|}{x} = \lim_{h \to 0^+} \frac{|h|}{h} = \lim_{h \to 0^+} \frac{h}{h} = 1$

Here, $\mathrm{RHL} \neq \mathrm{LHL}$, so the limit does not exist at $x=0$.

Existence of a Limit

From the example, we can define the existence of a limit:

The limit of $f(x)$ at $x=a$ exists if: $\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x)$
i.e., LHL = RHL at $x=a$.

Notice that the limit can exist even if $f(x)$ is not defined at $x=a$.

How to Calculate Left-Hand and Right-Hand Limits

Learn a step-by-step approach to calculating left-hand and right-hand limits, using formulas and one-sided limit techniques to accurately evaluate function behavior near a point.

Step-by-Step Approach for Limit Calculation

To calculate left-hand and right-hand limits, follow these steps:

1. Identify the point $x = a$ where you want to find the limit.

2. Determine whether you are approaching $a$ from the left ($x \to a^-$) or from the right ($x \to a^+$).

3. Substitute values close to $a$ from the chosen side into $f(x)$.

4. Simplify the expression and observe the value $f(x)$ is approaching.

For example, for $f(x) = \frac{|x|}{x}$ at $x=0$, approaching from the left gives $\mathrm{LHL} = -1$, and approaching from the right gives $\mathrm{RHL} = 1$.

Using Limit Formulas for LHL and RHL

Limit formulas make calculation easier, especially for common functions:

• $\lim_{x \to a^-} (x^n) = a^n$

• $\lim_{x \to a^+} (x^n) = a^n$

• $\lim_{x \to a^-} (k) = k$

• $\lim_{x \to a^+} (k) = k$

For piecewise functions, calculate LHL and RHL using the expression defined on that side of $x = a$.

Common Mistakes to Avoid While Calculating One-Sided Limits

• Forgetting which side you are approaching ($a^-$ vs $a^+$).

• Substituting $x = a$ directly in piecewise functions without checking the correct expression.

• Assuming LHL = RHL without verification.

• Ignoring discontinuities at the point.

Left-Hand and Right-Hand Limits Formulas

Below are the important formulas and limit laws for left-hand and right-hand limits, including standard limit expressions and methods to apply them to piecewise functions.

Standard Limit Formulas

Some common formulas for quick reference:

• $\lim_{x \to a} (x + b) = a + b$

• $\lim_{x \to a} (x - b) = a - b$

• $\lim_{x \to a} (kx) = ka$

• $\lim_{x \to a} (x^n) = a^n$

These work for both LHL and RHL when approaching from the respective sides.

Limit Laws for One-Sided Limits

The limit laws can be applied to one-sided limits as well:

1. Sum/Difference: $\lim_{x \to a^\pm} [f(x) \pm g(x)] = \lim_{x \to a^\pm} f(x) \pm \lim_{x \to a^\pm} g(x)$

2. Product: $\lim_{x \to a^\pm} [f(x)g(x)] = \lim_{x \to a^\pm} f(x) \cdot \lim_{x \to a^\pm} g(x)$

3. Quotient: $\lim_{x \to a^\pm} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a^\pm} f(x)}{\lim_{x \to a^\pm} g(x)}$, if $\lim_{x \to a^\pm} g(x) \neq 0$

How to Apply Formulas to Piecewise Functions

For piecewise functions, use the expression that corresponds to the side you are approaching:

• For LHL, use the expression defined for $x < a$.

• For RHL, use the expression defined for $x > a$.

Example:

$f(x) = \begin{cases} x^2, & x < 1 \\ 2x+1, & x > 1 \end{cases}$

Then: $\lim_{x \to 1^-} f(x) = 1^2 = 1$
$\lim_{x \to 1^+} f(x) = 2(1)+1 = 3$
Here, LHL $\neq$ RHL, so the limit does not exist at $x=1$.

How to Understand Limits Using Graphs

Visualize left-hand and right-hand limits with graphs, identify discontinuities, and analyze one-sided limits through clear, intuitive graphical representations.

Graphical Representation of LHL and RHL

A graph helps visualize how a function behaves near a point.

• The LHL is the value the curve approaches from the left side.

• The RHL is the value the curve approaches from the right side.

If the two values meet at the same height, the limit exists at that point.

Detecting Discontinuity Through Graphs

• Jump discontinuity occurs when LHL $\neq$ RHL.

• Removable discontinuity occurs when LHL = RHL, but $f(a)$ is undefined.

• Infinite discontinuity occurs when the function shoots off to infinity from either side.

Graphs make it easy to quickly spot discontinuities and verify one-sided limits visually.

Solved Examples Based on Left-Hand Limits and Right-Hand Limits

Example 1: Let $[x]$ denote the greatest integer less than or equal to $x$. Then $x \rightarrow 0 \left\lvert\, \lim\limits _{x \rightarrow 0} \frac{\tan \left(\pi \sin ^2 x\right)+(|x|-\sin (x[x]))^2}{x^2}\right.$ [JEE Mains 2019]
1) equals $\pi+1$
2) equals $0$
3) does not exist
4) equals $\pi$

Solution:
Evaluation of Trigonometric limit -

$
\begin{aligned}
& \lim\limits _{x \rightarrow a} \frac{\sin (x-a)}{x-a}=1 \\
& \lim\limits _{x \rightarrow a} \frac{\tan (x-a)}{x-a}=1
\end{aligned}
$

put $x=a+h$ where $h \rightarrow 0$
Then it comes

$
\begin{aligned}
& \lim\limits _{h \rightarrow 0} \frac{\sin h}{h}=\lim\limits _{h \rightarrow 0} \frac{\tanh }{h}=1 \\
& \therefore \lim\limits _{x \rightarrow 0} \frac{\sin x}{x}=1 \text { and } \\
& \therefore \quad \lim\limits _{x \rightarrow 0} \frac{\tan x}{x}=1
\end{aligned}
$

Right hand limit -

The right hand limit of $f(x)$ as ' $x$ ' tends to 'a' exists and is equal to $l_1$, if as '$x$' approaches '$a$' through values greater than '$a$'.

so $\lim\limits _{x \rightarrow a^{+}} f(x)=l_1$

wherein

$\mathrm{a}^{+}$means $\mathrm{a}+\mathrm{h} \space $&$ \mathrm{~h} \rightarrow 0$. Therefore $\mathrm{f}(\mathrm{a}+\mathrm{h})$.

Left-hand Limit -

The left-hand limit of $f(x)$ as ' $x$ ' tends to '$a$' exists and is equal to $l_2$, if as 'x' approaches '$a$' through values less than '$a$'.

$
\lim\limits _{x \rightarrow a^{-}} f(x)=l_2
$
Where $\mathrm{a}^{-}$means ( $\mathrm{a}-\mathrm{h}$ ) $h \rightarrow 0$. Therefore, $\mathrm{f}(\mathrm{a}-\mathrm{h})$.

$
\begin{aligned}
& \lim\limits _{x \rightarrow 0} \frac{\tan \left(\pi \sin ^2 x\right)+(|x|-\sin (x[x]))^2}{x^2} \\
& =\lim\limits _{x \rightarrow 0}\left[\frac{\tan \left(x \sin ^2 x\right)}{x \sin ^2 x} \times \simeq\left(\frac{\sin x}{x}\right)^2+\frac{x^2}{x^2}-\frac{2|x| \sin (x[x])}{x^2}+\frac{\sin ^2(x[x])}{x^2}\right]
\end{aligned}
$
RHS, $\lim\limits x \rightarrow 0+, \quad|x|=x$ and $[x]=0$
So, RHS $=(\pi+1)$
LHS, $\lim\limits x \rightarrow 0-,|x|=-x$ and $[x]=-1$
So, LHS $=(\pi+1-2+1)=\pi$

Hence limit does not exist

Hence, the answer is the option 3.

Example 2: Let $f: R \rightarrow P$ defined as $f(x)=\left\{\begin{array}{c}x^5 \sin \left(\frac{1}{x}+5 x^2\right), x<0 \\ 0, x=0 \\ x^5 \cos \left(\frac{1}{x}+\lambda z^2, x<0\right)\end{array}\right.$ The value of $\lambda$ for which $f^{\prime \prime}(x)$ exists is: [JEE Mains 2020]

1) $2$

2) $3$

3) $5$

4) $6$

Solution:
L.H.L $=$ R.H.L.

$
\begin{aligned}
& 2 \lambda=10 \\
& \lambda=5
\end{aligned}
$

Hence, the answer is option (3).

$
\begin{aligned}
& f^{\prime}(x)=\left\{\begin{array}{c}
5 x^4 \sin \left(\frac{1}{x}\right)-x^3 \cos \left(\frac{1}{x}\right)+10 x, x<0 \\
0, \quad x=0 \\
5 x^4 \cos \left(\frac{1}{x}\right)+x^3 \sin \left(\frac{1}{x}\right)+2 \lambda, x>0
\end{array}\right. \\
& f^{\prime \prime}(x)=\left\{\begin{array}{c}
\text { term having } \mathrm{x} \text { in muliplication }+10, x<0 \\
0, \quad x=0 \\
\text { term having } \mathrm{x} \text { in muliplication }+2 \lambda, x>0
\end{array}\right.
\end{aligned}
$

L.H.L = R.H.L.

$\begin{aligned} & 2 \lambda=10 \\ & \lambda=5\end{aligned}$

Hence, the answer is option (3).

Example 3: Let [t] denote the greatest integer. If for some $\lambda \epsilon R-[0,1]_{x \rightarrow 0} \lim\limits _{x \rightarrow 0}\left|\frac{1-x+|x|}{\lambda-x+[x]}\right|=L$, then L is equal to: [JEE Mains 2020]

1) $12$

2) $2$

3) $\frac{1}{2}$

4) $0$

Solution:

$
\begin{aligned}
& \lim\limits _{x \rightarrow 0}\left|\frac{1-x+|x|}{\lambda-x+\mid x]}\right|=L \\
& L H L=\lim\limits _{x \rightarrow 0}\left|\frac{1-2 x}{\lambda-x-1}\right|=\frac{1}{|\lambda-1|} \\
& R H L=\lim\limits _{x \rightarrow 0}\left|\frac{1}{\lambda-x-0}\right|=\frac{1}{|\lambda|} \\
& \therefore \frac{1}{|\lambda-1|}=\frac{1}{|\lambda|} \Rightarrow \lambda=\frac{1}{2} \\
& \therefore L=2
\end{aligned}
$
Hence, the answer is the option 1.

Example 4. ${\lim\limits _{x \rightarrow a} \frac{(a+2 x)^{1 / 3}-(3 x)^{1 / 3}}{(3 a+x)^{1 / 3}-(4 x)^{1 / 3}}(a \neq 0)}$ is equal to?
[JEE Mains 2020]
1) $\left(\frac{2}{3}\right)^{\frac{4}{3}}$
2) $\left(\frac{2}{3}\right)\left(\frac{2}{9}\right)^{\frac{1}{3}}$
3) $\left(\frac{2}{9}\right)^{\frac{4}{3}}$
4) $\left(\frac{2}{9}\right)\left(\frac{2}{3}\right)^{\frac{1}{3}}$

Solution:

$
\begin{aligned}
L & =\lim\limits _{h \rightarrow 0} \frac{(a+2(a+h))^{1 / 3}-(3(a+h))^{1 / 3}}{(3 a+a+h)^{1 / 3}-(4(a+h))^{1 / 3}} \\
& =\lim\limits _{h \rightarrow 0} \frac{(3 a)^{1 / 3}\left(1+\frac{2 h}{3 a}\right)^{1 / 3}-(3 a)^{1 / 3}\left(1+\frac{h}{a}\right)^{1 / 3}}{(4 a)^{1 / 3}\left(1+\frac{h}{4 a}\right)^{1 / 3}-(4 a)^{1 / 3}\left(1+\frac{h}{a}\right)^{1 / 3}} \\
& =\lim\limits _{h \rightarrow 0}\left(\frac{3^{1 / 3}}{4^{1 / 3}}\right)\left[\frac{\left(1+\frac{2 h}{9 a}\right)-\left(1+\frac{h}{3 a}\right)}{\left(1+\frac{h}{12 a}\right)-\left(1+\frac{h}{3 a}\right)}\right] \\
& =\left(\frac{3}{4}\right)^{1 / 3} \frac{\left(\frac{2}{9}-\frac{1}{3}\right)}{\left(\frac{1}{12}-\frac{1}{3}\right)}=\left(\frac{3}{4}\right)^{1 / 3}\left(\frac{8-12}{3-12}\right) \\
& =\left(\frac{3}{4}\right)^{1 / 3}\left(\frac{-4}{-9}\right)=\frac{4^{1-\frac{1}{3}}}{3^{2-\frac{1}{3}}}=\frac{4^{2 / 3}}{3^{5 / 3}}
\end{aligned}
$
$
L=\frac{(8 \times 2)^{1 / 3}}{(27 \times 9)^{1 / 3}}=\frac{2}{3}\left(\frac{2}{9}\right)^{1 / 3}
$

Hence, the answer is the option 2.

Example 5:Let $[\mathrm{t}]$ denote the greatest integer $\leq \mathrm{t}$ and t denote the fractional part of t . The integral value of $\alpha$ for which the left-hand limit of the function $\mathrm{f}(\mathrm{x})=[1+\mathrm{x}]+\frac{\alpha^{2[\mathrm{x}]+\{\mathrm{x}\}}+[\mathrm{x}]-1}{2[\mathrm{x}]+\{\mathrm{x}\}} \mathrm{x}=0$ is equal to $\alpha-\frac{4}{3}$, is [JEE Mains 2022]
1) $3$
2) $4$
3) $6$
4) $0$

Solution

$
\lim\limits _{x \rightarrow 0^{-}}[x]=-1, \lim\limits _{x \rightarrow 0^{-}}\{x\}=1
$
So $\lim\limits _{x \rightarrow 0^{-}} f(x)$

$
\begin{aligned}
& =\lim\limits _{x \rightarrow-}\left(1+[x]+\frac{\alpha^{2[x]+\{x\}}+[x]-1}{2[x]+\{x\}}\right)=\alpha-\frac{4}{3} \\
& \Rightarrow \quad 1-1+\frac{\alpha^{2(-1)+1}+(-1)-1}{2(-1)+1}=\alpha-\frac{4}{3} \\
& \Rightarrow \quad \frac{\frac{1}{\alpha}-2}{-1}=\alpha-\frac{4}{3} \Rightarrow-\frac{1}{2}+2=\alpha-\frac{4}{3} \\
& \Rightarrow \alpha+\frac{1}{\alpha}=\frac{10}{3} \Rightarrow 3 \alpha^2-10 \alpha+3=0 \\
& \Rightarrow \alpha=3 \text { OR } \alpha=1 / 3
\end{aligned}
$
Since $\alpha=$ integer,

$
\alpha=3
$
Hence, the answer is $3$

List of topics related to Left and Right Hand Limits

Explore all the essential topics related to left-hand and right-hand limits, including, to build a strong foundation. In this section, we have given the list of topics related to left and right-hand limits:

Indeterminate Forms

Limits of Trigonometric Functions

Limits using expansion

Algebra of Limits

Higher Order Derivatives: Formula, Definition, Examples

NCERT Resources

We have provided below complete NCERT notes, solutions, and exemplar problems for Limits and Derivatives. These study materials follow the latest CBSE guidelines and help build strong clarity for board exams and competitive exams.

NCERT Notes for Class 11 Maths Chapter 13 - Limits and Derivatives

NCERT Solutions for Class 11 Maths Chapter 13 - Limits and Derivatives

NCERT Exempar Solutions for Class 11 Maths Chapter 13 - Limits and Derivatives

Practice Questions based on Left and Right Hand Limits

Test your understanding with carefully designed practice questions on left-hand and right-hand limits, featuring step-by-step solutions and examples to master one-sided limits effectively.

Left Hand Limits And Right Hand Limits - Practice Question MCQ

We have shared the links below to practice questions on the related topics of left and right hand limits: