Measuring Angles

In geometry, an angle is made when there are two rays meeting at a common point, known as a vertex. Angle are usually measured in radians or degrees.

In this article, we will learn more about the concept of measurement of angles. This category is under the branch of trigonometry. It is an important chapter for the syllabus of Class 11th mathematics. It is essential for both the perspective of board exams and compeititve level exams such as JEE Main, WBJEE, BITSAT, etc.

This Story also Contains

1. What is an Angle?
2. Types of Angles
3. Measurement of angle
4. How do we measure an Angle?
5. The Relation between Degree and Radian Measures
6. Interconversion of units
7. Solved Examples Based on Measurement of Angles

What is an Angle?

An angle is a figure in two dimensional geometry, which is formed by two rays meeting each other at a common point known as vertex. It is derived from a Latin word “Angulus”, meaning “corner”, which mean “angle” in English.

The two rays that meet at a common point are called the sides of an angle. The symbol "∠" is used to indicate the angle. The Greek letters θ, α, β, etc., can be used to indicate the angle measurement between the two rays.

If the angles are measured from the line, it is categorized into two parts :

1. Positive Angle
2. Negative angle

Positive angle -If the angle is measured in an anticlockwise direction it is called a Positive angle.

Negative angle - If the angle is measured in a clockwise direction it is known as a negative angle.

Some commonly used terms in angles are

• Initial side: the original ray
• Terminal side: the final position of the ray after rotation
• Vertex: point of rotation

Types of Angles

There are majorly six types of angles in Geometry. The names of all angles with their properties are:

• Acute Angle: It lies between 0° to 90.
• Obtuse Angle: It lies between 90° to 180°
• Right Angle: The angle which is exactly equal to 90°
• Straight Angle: The angle which is exactly equal to 180°
• Reflex Angle: The angle which is greater than 180° and less than 360°
• Complete Angle: The complete rotation of angle equal to 360°.

Measurement of angle

In order to draw an angle, start by drawing two rays. Fix one ray in a place, and then rotate the other ray. The fixed ray is known as the initial side, while the rotated ray is the terminal side. And the measure of angle is amount of rotation from intitial to the terminal side.

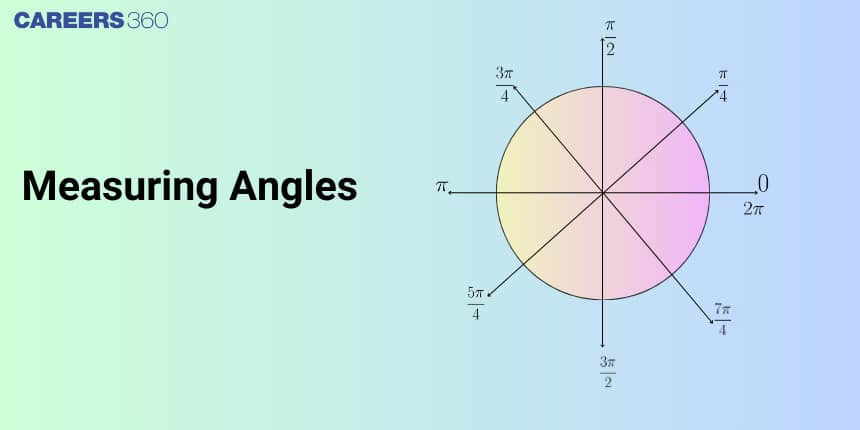
An angle in standard position is if its vertex is located at the origin and initial side extends to positive $x$ axis. It can be seen in the figure below:

If the angle is measured in a counterclockwise direction from the initial side to the terminal side, the angle is said to be a positive angle.

If the angle is measured in a clockwise direction, the angle is said to be a negative angle.

How do we measure an Angle?

To measure an angle, there are basic mathematical tools such as protractor and compass. A protractor is used to provide the exact measure of angle and compass helps in constructing an angle. An angle can be measured in three ways namely as degrees, radians and revolution.

Degrees

Degree is unit of measure of angle. It is measured using a tool known as protractor. It is denoted by the symbol, '°'. A circle revolves completely at 360°, as the circle divides itself into 360 equal parts.

Radians

Radian is a measurement unit of angle, is used as an alternative of degrees. Radian is the ratio of length of arc which the angle subtends on a circle, divided by length of radius of the circle. Radian is an angle subtended by the arc of the length of the radius of the same circle at the center and the ratio will give the radian measure of the angle. Radian is denoted as rad.

Revolution

A circle completes its full revolution and has 360° as subdivision of circle. It refers to some full rotation of 360 degrees.

The Relation between Degree and Radian Measures

By the definitions of degree and radian measures, we know that the angle subtended by a circle at the centre is:

• 360° – according to degree measure
• 2π radian – according to radian measure

Hence, 2π radian = 360° ⇒ π radian = 180°. Now, we substitute the approximate value of π as 227 in the equation above and get, 1 radian = 180°π = 57° 16′ approximately. Also, 1° = π180° radian = 0.01746 radian approximately.

The system used for the measurement of angles

There are three systems used for the measurement of angles

1. Sexagesimal System

2. Centesimal system

3. Circular system

1. Sexagesimal system

In this system, an angle is measured in degrees, minutes, and seconds.

1 Right angle = 90^o (Read as 90 degrees)

1^o = 60’ ( 1 degree = 60 minutes)

1’ = 60” ( 1 minutes = 60 seconds)

2. Centesimal system

In this system, the measurement of the right angle is divided into 100 equal parts, and parts called Grades.

1 Right angle = 100g (Read as 100 grades)

3. Circular system

In this system, an angle is measured in radians.

One radian is the measure of the central angle of a circle that intercepts an arc equal in length to the radius of that circle. A central angle is an angle formed at the centre of a circle by two radii.

The formula for the radian measure of an angle formed by an arc of length l at the centre of the circle of radius r is (Length of arc)/(Radius) = l/r

Because the total circumference equals 2π times the radius, a full circular rotation is 2π radians.

So, 2π radians = 360°

So, π radians = 360°/ 2 = 180°

and 1 radian = 180°/ π ≈ 57.3°

Interconversion of units

1. Degree to Radian

Since, degrees and radians both measure angles, we need to be able to convert between them. We can easily do so using a proportion (where θ is the measure of the angle in degrees and θ_R is the measure of the angle in radians)

$\frac{\theta}{180}=\frac{\theta_{\mathrm{R}}}{\pi}$

Or

$\frac{\text { Degree }}{180}=\frac{\text { Radians }}{\pi}$

Note:

(i) Radian is the unit to measure angles, and it does not mean that π stands for 180^o. π is a real number. Remember the relation, π radians = 180^o.

(ii) In a circle of radius r, the length of an arc s is subtended by an angle with measure θ in radians. Arc length = (radius) x (Angle subtended by an arc in radians)

$\mathrm{s}=\mathrm{r} \theta$

2. Degree to grades

If we denote the number of degrees by D and the number of grades by G, the relation between them is given by

$\frac{D}{90}=\frac{G}{100}$

3. Radian to Grades

If the number of radians is represented by $R$ and the number of grades is represented by G, the relation between Radian and Grades is given by

$\frac{G}{100}=\frac{2 * R}{\pi}$

Measurement of angles using Protractor

An angle is measured by using two geometric tools - a protractor and a compass. While a protractor can be used for both constructing and measuring, a compass is mostly used for constructing an angle. A protractor is considered one of the most important geometric tools as it helps in measuring angles in both degrees and radians

The steps to measure an angle are:

Step 1: Place the centre of the protractor on the vertex of the angle.

Step 2: Superimpose one side of the angle with the zero line of the protractor.

Step 3: The angle is equal to the number of degrees crossed on the protractor.

Constructing Angles Using a Protractor

A protractor can be used not only for measuring but also for constructing angles. This helps in both measuring the angles accurately and learning how to use the protractor.

The steps to construct an Angle:

Step 1: Draw a baseline.

Step 2: Mark the point O and place the centre of the protractor at O.

Step 3: Align the baseline of the protractor with the line.

Step 4: In the inner readings, look for the angle to be constructed and mark it as point C.

Step 5: Now using a scale, join O and C.

Summary

Measuring angles is a basic concept of geometry and trigonometry. It is essential for understanding relationships and solving variety of mathematical and practical problems. Accurate angle measurement is necessary for precise calculations.

Solved Examples Based on Measurement of Angles

Example 1: What is the shortest positive measure of the angle (in degrees) formed between the positive x-axis and the line if the total angle elapsed is $810^{\circ}$?

Solution: Total angle elapsed $=810^{\circ}$
Total angle elapsed in two revolutions $=720^{\circ}$
Thus, the angle $=810^{\circ}-720^{\circ}=90^{\circ}$
Hence, the answer is 90.

Example 2: What is the value of the radius of a circle if the circumference is $\frac{8 \pi}{3}$?
Solution: Since the formula for circumference $=2 \pi r$
Thus, $r=\frac{4}{3}$
Hence the answer is $\frac{-4}{3}$

Example 3: The angles of a triangle are in the ratio $2: 3: 5$. Find the least/minimum angle in radians.

Solution: Let the angles be $2 \mathrm{x}, 3 \mathrm{x}, 5 \mathrm{x}$.
Thus sum $=10 \mathrm{x}=1800$

$\Rightarrow x=180=18 \times \frac{\pi}{180}=\frac{\pi}{10} \mathrm{rad}$
Minimum angle $=2 x=2 \times \frac{\pi}{10}=\frac{\pi}{5}$ radians.
Hence the answer is $\frac{\pi}{5}$ radian.

Example 4: If the radius of the circle = $\frac{1}{2} x$ circumference subtended by an angle A . Find the measure of angle A.

Solution: Circumference subtended by an angle = arc length

Also given that

$r = \frac{I}{2}$

So, $\frac{l}{r} = 2$

$A = 2$ radian (as $\frac{l}{r} = angle in radians)

Hence the answer is $2$ radian

Example 5: A circular wire of radius 3 cm is cut and bent so as to lie along a circle of radius 48 cm. Find the angle subtended by the wire at the centre of the circle.

Solution: Length of the circular wire $=2 \pi r=6 \pi \mathrm{cm}$.
The angle subtended by the arc at the center $=\frac{a r c}{\text { radius }}$

$\Rightarrow \frac{6 \pi}{48}=\frac{\pi}{8} \text { radian }$
Hence, the answer is $\frac{\pi}{8}$ radian.