Law Of Tangents: Definition, Proof, Formula and Examples

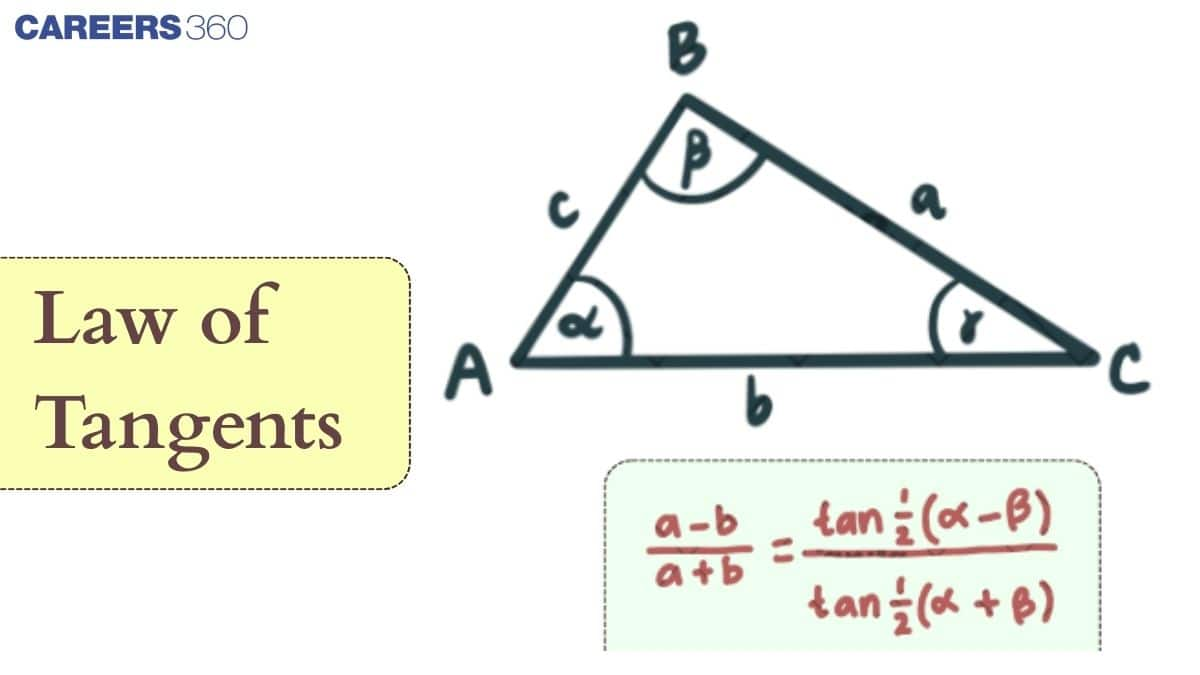
Overview of Law of Tangent

The tangent rule states that the ratio of the difference and sum of any two angles of a triangle is equal to the ratio of the difference and sum of the sides opposite to those angles. In other words, it establishes a relationship between the tangents of two angles of a triangle and the lengths of the sides opposite to them.

Tangent Rule Definition

The law of tangents, or tangent rule, expresses the relationship between the tangents of two angles of a triangle and the lengths of their opposite sides. It is particularly useful when two sides and the included angle, or two angles and a side, are known. Using this rule, we can compute the unknown angles of a triangle when two sides $a$ and $b$ and the enclosed angle $C$ are given.

The formula can be expressed as:

$\frac{a - b}{a + b} = \frac{\tan \frac{1}{2}(A - B)}{\tan \frac{1}{2}(A + B)}$

Here,

• $a$ and $b$ are two sides of the triangle

• $\angle A$ and $\angle B$ are the angles opposite those sides

This equation helps in finding unknown sides or angles with fewer steps than other trigonometric identities.

Tangent Rule Formula Proof

To prove this, we use the sine rule and the formula for sum/difference into the product of sine and cosine.

From the sine rule:

$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $

$ \Rightarrow \frac{\sin B}{\sin C} = \frac{b}{c} $

Using Componendo and Dividendo theorem:

$ \Rightarrow \frac{\sin B - \sin C}{\sin B + \sin C} = \frac{b-c}{b+c} $

Using sum/difference into product formula:

$ \Rightarrow \frac{2 \cos \frac{B+C}{2} \sin \frac{B-C}{2}}{2 \sin \frac{B+C}{2} \cos \frac{B-C}{2}} = \frac{b-c}{b+c} $

$ \Rightarrow \cot \frac{B+C}{2} \cdot \tan \frac{B-C}{2} = \frac{b-c}{b+c} $

$ \Rightarrow \tan \frac{A}{2} \cdot \tan \frac{B-C}{2} = \frac{b-c}{b+c} $

$ \left[ \because \frac{B+C}{2} = \frac{\pi - A}{2} \Rightarrow \cot \frac{B+C}{2} = \cot \left(\frac{\pi}{2} - \frac{A}{2}\right) = \tan \frac{A}{2} \right] $

$ \Rightarrow \frac{\tan \frac{B-C}{2}}{\cot \frac{A}{2}} = \frac{b-c}{b+c} $

$ \Rightarrow \tan \frac{B-C}{2} = \frac{b-c}{b+c} \cot \frac{A}{2} $

By using the same method, other formulas can also be proved.

So, in triangle ABC, we have:

$ \tan \frac{A-B}{2} = \frac{a-b}{a+b} \cot \frac{C}{2} $

$ \tan \frac{B-C}{2} = \frac{b-c}{b+c} \cot \frac{A}{2} $

$ \tan \frac{C-A}{2} = \frac{c-a}{c+a} \cot \frac{B}{2} $

These formulas are collectively known as the Tangent Rule. They are especially useful for calculating the unknown parts of a triangle when certain sides or angles are given.

The law of tangents (tan rule) can be applied in the following cases:

1. When two sides and one angle are given

2. When two angles and one side are given

3. When all three sides are given

4. When two sides and the angle between them are given

Relation with Law of Sines and Law of Cosines

• The Law of Sines deals with ratios of sides and their opposite angles:
  $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

• The Law of Cosines connects sides with the cosine of an angle:
  $c^2 = a^2 + b^2 - 2ab \cos C$

• The Law of Tangents proof shows that it can actually be derived by manipulating the Law of Sines.

Thus, the three laws together: Sine, Cosine, and Tangent, form a powerful formula set for solving any type of triangle.

Solved Examples Based on Tangent Rule

Example 1: In a $\triangle A B C$, the sides $\mathrm{a}=4, \mathrm{~b}=2$ and $\angle c=90^{\circ}$. To find the value of $A-B$.
Solution:

Given that:

$ a = 4, \quad b = 2, \quad \text{and } \angle C = 90^\circ $

We know that:

$ \angle A + \angle B + \angle C = 180^\circ $

$ \angle A + \angle B = 180^\circ - \angle C $

$ \angle A + \angle B = 90^\circ $

By the law of tangents:

$ \frac{a-b}{a+b} = \frac{\tan \frac{A-B}{2}}{\tan \frac{A+B}{2}} $

Putting the values in the equation:

$ \frac{4-2}{4+2} = \frac{\tan \frac{1}{2}(A-B)}{\tan \frac{1}{2}(90^\circ)} $

$ \frac{2}{6} = \frac{\tan \frac{1}{2}(A-B)}{\tan 45^\circ} $

$ \frac{1}{3} \tan 45^\circ = \tan \frac{1}{2}(A-B) $

Solving:

Since $x$ is in the first quadrant, $\cos x$ is positive.

Substituting the value of $\sec x = \frac{4}{3}$ to get:

$ \tan x = \pm \sqrt{\left(\frac{4}{3}\right)^2 - 1} $

$ \tan x = \sqrt{\frac{7}{9}} $

Hence, the answer is $\sqrt{\frac{7}{9}}$

Example 2: With the usual notation, in $\triangle A B C$, if $\angle A+\angle B=120^{\circ}, a=\sqrt{3}+1$ and $b=\sqrt{3}-1$, then the ratio $\angle A: \angle B$, is:

Solution:

We know the Addition Formulae $\sin (A+B)=\sin A \cos B+\cos A \sin B$

Given $\angle A+\angle B=120^{\circ}$

Using Napier’s Analogy:

$ \tan \frac{A-B}{2} = \frac{a-b}{a+b} \cot \frac{C}{2} $

$ \tan \frac{A-B}{2} = \frac{\sqrt{3}+1 - (\sqrt{3}-1)}{2\sqrt{3}} \cot 30^\circ $

$ \tan \frac{A-B}{2} = 1 $

We know: $ \tan 45^\circ = 1 $

So: $ \frac{A-B}{2} = 45^\circ $

$ \Rightarrow \angle A- \angle B = 90^\circ $

From (1) and (2):

$ \Rightarrow \angle A = 105^\circ, \quad \angle B = 15^\circ $

Hence, the answer is: $ 7:1 $

Example 3: If $\cot \frac{B+C}{2} \cdot \tan \frac{B-C}{2}=x, \text { then } \mathrm{x} \text { equals. }
$

Solution:

We know the tangent rule:

$ \tan \frac{B-C}{2} = \frac{b-c}{b+c} \cot \frac{A}{2} $

Multiply both sides by $\tan \frac{A}{2}$:

$ \tan \frac{A}{2} \tan \frac{B-C}{2} = \frac{b-c}{b+c} $

From triangle $ABC$:

$ \angle A + \angle B + \angle C = \pi $

$ \angle A = \pi - (B + C) $

Putting the value of $A$ in the equation:

$ \tan \frac{\pi - (B+C)}{2} \tan \frac{B-C}{2} = \frac{b-c}{b+c} $

We know $\tan(\pi/2 - A) = \cot A$:

$ \cot \frac{B+C}{2} \tan \frac{B-C}{2} = \frac{b-c}{b+c} $

Hence:

$ x = \frac{b-c}{b+c} s $

Hence, the answer is $\frac{b-c}{b+c}$

Example 4: Solve: $\cot \frac{A+B}{2} \cdot \tan \frac{A-B}{2}=$ ?

Solution:

According to Napier's Analogy, for any $\triangle ABC$:

$ \tan \frac{A-B}{2} = \frac{a-b}{a+b} \cot \frac{C}{2} $

$ \tan \frac{B-C}{2} = \frac{b-c}{b+c} \cot \frac{A}{2} $

$ \tan \frac{C-A}{2} = \frac{c-a}{c+a} \cot \frac{B}{2} $

We know:

$ \tan \frac{A-B}{2} = \frac{a-b}{a+b} \cot \frac{C}{2} \quad \ldots (i) $

$ \angle A + \angle B + \angle C = \pi $

$ \frac{1}{2}(A+B) = \frac{1}{2}(\pi - C) $

$ \tan \frac{A+B}{2} = \tan \frac{\pi - C}{2} $

$ \tan \frac{A+B}{2} = \cot \frac{C}{2} $

By equation (i):

$ \tan \frac{A-B}{2} = \frac{a-b}{a+b} \tan \frac{A+B}{2} $

$ \cot \frac{A+B}{2} \cdot \tan \frac{A-B}{2} = \frac{a-b}{a+b} $
Hence, the answer is $\frac{a-b}{a+b}$.

Example 5: If $\sec x=\frac{4}{3},x$ is in the first quadrant, find the value of $\tan x$.

Solution:

Given that,

$\sec x = \frac{4}{3}$

Using the tangent formula,

$\tan x = \pm \sqrt{\sec^2 x - 1}$

Since $x$ is in the first quadrant, $\tan x$ is positive. Thus,

Substituting $\sec x = \frac{4}{3}$, we get

$\tan x = \sqrt{\left(\frac{4}{3}\right)^2 - 1}$

$\tan x = \sqrt{\frac{16}{9} - 1}$

$\tan x = \sqrt{\frac{7}{9}}$

$\tan x = \frac{\sqrt{7}}{3}$

List of Topics related to Law of Tangents

The Law of Tangents links with multiple trigonometric concepts that extend its applications beyond basic triangle problems. Exploring these topics strengthens problem-solving skills and provides a deeper grasp of trigonometric methods. Below are the related topics you can practice.

NCERT Resources

NCERT resources are highly useful for building a strong understanding of trigonometric functions. They present concepts in a clear manner, offer worked-out examples, and include practice problems for thorough learning. Below are the NCERT resources for Chapter 3: Trigonometric Functions.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3 - Trigonometric Functions

Practice Questions based on Law of Tangents

Solving MCQs on the Law of Tangents and related trigonometric topics helps sharpen problem-solving skills and boosts exam readiness. These practice sets are designed to stregthen concepts and improve speed and accuracy. Below are the topics you can explore for targeted practice.

Law Of Tangents - Practice Question MCQ

You can practice questions on related topics from the links shared below: