Maximum and Minimum value of Trigonometric Function
The maximum and minimum values of trigonometric functions play a key role in solving mathematical problems related to $\sin \theta, \cos \theta, \sin \theta \cos \theta$, and $\sec \theta$. By knowing these limits, students can easily handle questions involving equations, inequalities, and graphs of trigonometric functions. For instance, the maximum value of $\cos \theta$ is 1, while the minimum value of $\sec \theta$ is also derived from these fundamental properties. In this article, we will cover the important formulas, solved examples, practice questions, and related resources to strengthen your understanding in mathematics.
This Story also Contains
- What are the maximum and minimum values in trigonometry?
- Standard Values of Trigonometric Functions
- Basic Maximum and Minimum Values of Standard Trigonometric Functions
- Maximum and Minimum Value of Trigonometric Expressions
- Graphical Approach to Finding Maximum and Minimum Values
- Standard Trigonometric Values Table
- List of Topics Related to the Maximum And Minimum Value Of Trigonometric Functions
- NCERT Resources
- Practice Questions on Maximum And Minimum Value Of Trigonometric Function
What are the maximum and minimum values in trigonometry?
Functions like $\sin \theta$ and $\cos \theta$ vary between $-1$ and $1$, while $\tan \theta$ and $\cot \theta$ extend to $\infty$ and $-\infty$. Reciprocal functions such as $\sec \theta$ and $\csc \theta$ are restricted to values $\geq 1$ or $\leq -1$.
Maximum and minimum values help in simplifying equations like $a \sin \theta + b \cos \theta$ and in checking the validity of trigonometric inequalities.
Graphs of $\sin \theta$, $\cos \theta$, and $\sec \theta$ make it easy to visualize their range and quickly identify maxima and minima.
Standard Values of Trigonometric Functions
The domain of trigonometric functions $θ$ can be expressed in both degrees and radians. Certain specific values of $θ$, often referred to as standard values or principal values, are widely used in solving problems of trigonometry. These values are derived from the unit circle approach and are essential for evaluating maximum and minimum values of trigonometric functions.
Maximum and Minimum Value of $\sin x$ and $\cos x$
We know that the range of $\sin x$ and $\cos x$ is: $[-1, 1]$
This property forms the basis for analyzing and finding extreme values of more complex trigonometric expressions.
Transformation of $a \sin x + b \cos x$ into Single Trigonometric Form
When we deal with a function of the form:
$a \sin x + b \cos x$
We use the identity transformation:
Replace $a$ with $r \cos \theta$
Replace $b$ with $r \sin \theta$
Thus,
$a \sin x + b \cos x &= r \cos \theta \sin x + r \sin \theta \cos x$
$= r (\cos \theta \sin x + \sin \theta \cos x)$
$= r \sin(x + \theta)$
where, $r = \sqrt{a^2 + b^2}, \quad \tan \theta = \frac{b}{a}$
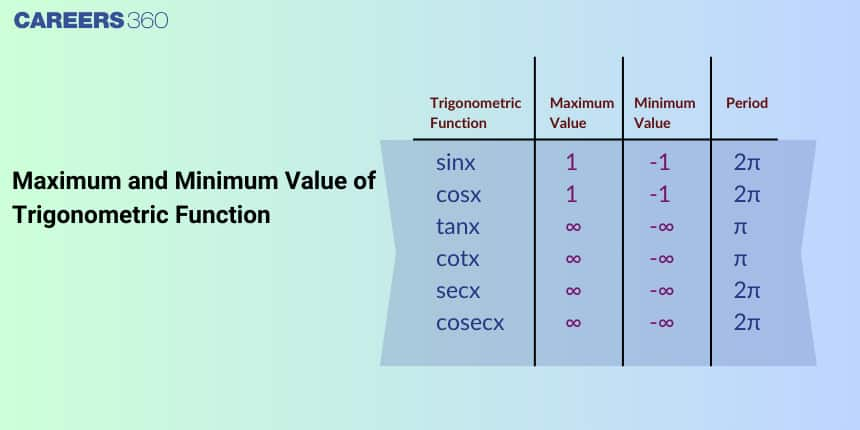
Basic Maximum and Minimum Values of Standard Trigonometric Functions
Standard trigonometric functions like $\sin \theta$, $\cos \theta$, $\tan \theta$, $\cot \theta$, $\sec \theta$, and $\csc \theta$ have well-defined maximum and minimum values within their domains. Below are the principal results that are frequently used in problem solving.
Maximum and Minimum Value of $\sin \theta$
The function $\sin \theta$ oscillates between $-1$ and $1$ for all real values of $\theta$.
Maximum value of $\sin \theta = 1$
Minimum value of $\sin \theta = -1$
This range is extremely important in solving problems related to periodic motion, waves, and inequalities.
Maximum and Minimum Value of $\cos \theta$
The function $\cos \theta$ also has its range confined to $[-1, 1]$.
Maximum value of $\cos \theta = 1$
Minimum value of $\cos \theta = -1$
Since $\cos \theta$ is a shifted version of $\sin \theta$, the results are similar but phase-shifted.
Maximum and Minimum Value of $\tan \theta$ and $\cot \theta$
The tangent function $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$ is unbounded.
Range of $\tan \theta = (-\infty, \infty)$
No maximum or minimum value exists, but $\tan \theta$ is undefined when $\cos \theta = 0$.
Similarly, for cotangent $\cot \theta = \dfrac{\cos \theta}{\sin \theta}$:
Range of $\cot \theta = (-\infty, \infty)$
No maximum or minimum value exists, but $\cot \theta$ is undefined when $\sin \theta = 0$.
Maximum and Minimum Value of $\sec \theta$ and $\csc \theta$
Both secant and cosecant are reciprocal functions:
$\sec \theta = \dfrac{1}{\cos \theta}$
$\csc \theta = \dfrac{1}{\sin \theta}$
Their ranges are unbounded but exclude $(-1, 1)$.
Range of $\sec \theta$: $(-\infty, -1] \cup [1, \infty)$
Range of $\csc \theta$: $(-\infty, -1] \cup [1, \infty)$
Thus, they have no global maximum or minimum, but they are bounded away from zero.
Deriving the Maximum and Minimum Values
Since the range of $\sin(x+\theta)$ is $[-1, 1]$, multiplying through by $r$ gives:
$-r \leq r \sin(x+\theta) \leq r$
Substituting $r = \sqrt{a^2 + b^2}$:
$-\sqrt{a^2+b^2} \leq a \sin x + b \cos x \leq \sqrt{a^2+b^2}$
Therefore:
Maximum value: $\sqrt{a^2+b^2}$
Minimum value: $-\sqrt{a^2+b^2}$
Maximum and Minimum Value of Trigonometric Expressions
Trigonometric expressions like $\sin \theta + \cos \theta$, $\sin \theta \cos \theta$, or $a \sin \theta + b \cos \theta$ often have fixed maximum and minimum values. Below are the key results and formulas to evaluate such expressions quickly.
Maximum and Minimum Value of $\sin \theta + \cos \theta$
We know that: $\sin \theta + \cos \theta = \sqrt{2} \sin\left(\theta + \frac{\pi}{4}\right)$
Hence,
Maximum value $= \sqrt{2}$
Minimum value $= -\sqrt{2}$
Maximum and Minimum Value of $\sin \theta \cos \theta$
Using the identity: $\sin \theta \cos \theta = \dfrac{1}{2} \sin 2\theta$
So the range is: $[-\tfrac{1}{2}, \tfrac{1}{2}]$
Thus,
Maximum value $= \tfrac{1}{2}$
Minimum value $= -\tfrac{1}{2}$
Maximum and Minimum Value of $a \sin \theta + b \cos \theta$
As derived earlier:
$a \sin \theta + b \cos \theta = \sqrt{a^2+b^2} \sin(\theta + \alpha)$, where $\tan \alpha = \tfrac{b}{a}$
Hence,
Maximum value $= \sqrt{a^2+b^2}$
Minimum value $= -\sqrt{a^2+b^2}$
Maximum and Minimum Value of Quadratic Trigonometric Forms
For quadratic forms like $a \sin^2 \theta + b \cos^2 \theta$, we use the identity:
$\sin^2 \theta + \cos^2 \theta = 1$
Thus,
$a \sin^2 \theta + b \cos^2 \theta = b + (a-b)\sin^2 \theta$
Since $\sin^2 \theta \in [0,1]$, the expression takes values between:
Minimum $= \min(a, b)$
Maximum $= \max(a, b)$
Graphical Approach to Finding Maximum and Minimum Values
Graphs of trigonometric functions make it simple to spot their highest and lowest values. Below are graphical methods to understand maxima and minima of $\sin \theta$, $\cos \theta$, $\tan \theta$, $\cot \theta$, $\sec \theta$, and $\csc \theta$.
Using Graphs of $\sin \theta$ and $\cos \theta$
The wave-like behavior of $\sin \theta$ and $\cos \theta$ shows their bounded nature. From the graph:
Peaks correspond to maximum $= 1$
Troughs correspond to minimum $= -1$
These graphs make it easier to visualize oscillations and identify extreme points.
Behavior of $\tan \theta$, $\cot \theta$, $\sec \theta$, and $\csc \theta$
The graph of $\tan \theta$ shows that it grows unbounded near $\theta = \frac{\pi}{2}, \frac{3\pi}{2}, ...$
The graph of $\cot \theta$ also diverges, but with vertical asymptotes at $\theta = 0, \pi, ...$
$\sec \theta$ and $\csc \theta$ graphs confirm that their values always lie outside $[-1, 1]$, showing discontinuities at undefined points.
This graphical perspective is crucial in competitive exams where visualization saves time.
Standard Trigonometric Values Table
The table below provides the standard values of trigonometric functions at specific angles ($0^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, $90^\circ$, $180^\circ$), which are crucial in solving maximum–minimum problems.
| t-function | $0^{\circ}$ | $30^{\circ}, \left(\frac{\pi}{6}\right)$ | $45^{\circ}, \left(\frac{\pi}{4}\right)$ | $60^{\circ}, \left(\frac{\pi}{3}\right)$ | $90^{\circ}, \left(\frac{\pi}{2}\right)$ | $180^{\circ}, (\pi)$ |
|---|---|---|---|---|---|---|
| $\sin \theta$ | $0$ | $\tfrac{1}{2}$ | $\tfrac{1}{\sqrt{2}}$ | $\tfrac{\sqrt{3}}{2}$ | $1$ | $0$ |
| $\cos \theta$ | $1$ | $\tfrac{\sqrt{3}}{2}$ | $\tfrac{1}{\sqrt{2}}$ | $\tfrac{1}{2}$ | $0$ | $-1$ |
| $\tan \theta$ | $0$ | $\tfrac{1}{\sqrt{3}}$ | $1$ | $\sqrt{3}$ | undefined | $0$ |
| $\csc \theta$ | undefined | $2$ | $\sqrt{2}$ | $\tfrac{2}{\sqrt{3}}$ | $1$ | undefined |
| $\sec \theta$ | $1$ | $\tfrac{2}{\sqrt{3}}$ | $\sqrt{2}$ | $2$ | undefined | $-1$ |
| $\cot \theta$ | undefined | $\sqrt{3}$ | $1$ | $\tfrac{1}{\sqrt{3}}$ | $0$ | undefined |
Solved Examples Based on the Maximum and Minimum Value of the Trigonometric Function
1) 4
2) $4 \sqrt{2}$
3) $\sqrt{34}$
4) None of these
Solution:
Maximum and minimum values:
The maximum and minimum values of $a \cos \Theta+b \sin \Theta$
$
\begin{aligned}
& \text { Max. value }=\sqrt{a^2+b^2} \\
& f(n)=5\left(\frac{\sin x}{\sqrt{2}}+\frac{\cos x}{\sqrt{2}}\right)+3\left(\frac{\cos x}{\sqrt{2}}-\frac{\sin x}{\sqrt{2}}\right) \\
& =\sqrt{2} \sin x+4 \sqrt{2} \cos x \\
& \text { Max value }=\sqrt{\sqrt{2}^2+4 \sqrt{2}^2}=\sqrt{34}
\end{aligned}
$
Hence, the correct option is option 3.
Example 2: Find out the range of function $4 \sin x-\sin ^2 x-1$
1) $[-1,2]$
2) $[-1,4]$
3) $[-6,2]$
4) $[-6,1]$
Solution:
Maximum and Minimum Value of Trigonometric Function
We know that range of $\sin \mathrm{x}$ and $\cos \mathrm{x}$ which is $[-1,1]$,
If there is a trigonometric function in the form of a $\sin \mathrm{x}+\mathrm{b} \cos \mathrm{x}$, then replace a with $\mathrm{r} \cos \theta$ and b with $\mathrm{r} \sin \theta$.
$
\begin{aligned}
a \sin \mathrm{x}+b \cos \mathrm{x} & =r \cos \theta \sin \mathrm{x}+r \sin \theta \cos \mathrm{x} \\
& =r(\cos \theta \sin \mathrm{x}+\sin \theta \cos \mathrm{x}) \\
& =r \sin (\mathrm{x}+\theta)
\end{aligned}
$
Then we have, where $r=\sqrt{a^2+b^2}$ and, $\tan \theta=\frac{\mathrm{b}}{\mathrm{a}}$
Since, $-1 \leq \sin (x+\theta) \leq 1$
Multiply with ' r '
$
\begin{aligned}
& \Rightarrow-\mathrm{r} \leq \sin (\mathrm{x}+\theta) \leq \mathrm{r} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq \sin (\mathrm{x}+\theta) \leq \sqrt{a^2+b^2} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq a \sin \mathrm{x}+b \cos \mathrm{x} \leq \sqrt{a^2+b^2}
\end{aligned}
$
So, the minimum value of the trigonometric function $\mathrm{a} \sin \mathrm{x}+\mathrm{b} \cos \mathrm{x}$ is $-\sqrt{a^2+b^2}$ and the maximum value is $\sqrt{a^2+b^2}$.
$4 \sin x-\sin ^2 x-1=-(\sin x-2)^2+3$
Range of this function is $[-6,2]$
Hence, the answer is option 3.
Example 3: Find the minimum value of $\sin 2 x+\csc 2 x \quad x \in\left[0, \frac{\pi}{2}\right]$
1) $-\infty$
2) -2
3) 2
4) 1
Solution:
Maximum and Minimum Value of Trigonometric Function
We know that range of $\sin x$ and $\cos x$ which is $[-1,1]$
If there is a trigonometric function in the form of a $\sin x+b \cos x$, then replace a with $\mathrm{r} \cos \theta$ and b with $\mathrm{r} \sin \theta$.
$
\begin{aligned}
a \sin \mathrm{x}+b \cos \mathrm{x} & =r \cos \theta \sin \mathrm{x}+r \sin \theta \cos \mathrm{x} \\
& =r(\cos \theta \sin \mathrm{x}+\sin \theta \cos \mathrm{x}) \\
& =r \sin (\mathrm{x}+\theta)
\end{aligned}
$
Then we have, where $r=\sqrt{a^2+b^2}$ and, $\tan \theta=\frac{\mathrm{b}}{\mathrm{a}}$
$
\begin{aligned}
& \text { Since, }-1 \leq \sin (\mathrm{x}+\theta) \leq 1 \\
& \text { Multiply with }{ }^{\prime} \mathrm{r}^{\prime} \\
& \Rightarrow-\mathrm{r} \leq \sin (\mathrm{x}+\theta) \leq \mathrm{r} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq \sin (\mathrm{x}+\theta) \leq \sqrt{a^2+b^2} \\
& \Rightarrow-\sqrt{a^2+b^2} \leq a \sin \mathrm{x}+b \cos \mathrm{x} \leq \sqrt{a^2+b^2}
\end{aligned}
$
So, the minimum value of the trigonometric function $a \sin x+b \cos x$ is $-\sqrt{a^2+b^2}$ and the maximum value is $\sqrt{a^2+b^2}$.
we know $A \cdot M . \geq G . M$.
$
\frac{\sin 2 x+\csc 2 x}{2} \geq(\sin 2 x \cdot \csc 2 x)^{\frac{1}{2}}
$
$
\sin 2 x+\csc 2 x \geq 2
$
Hence, the answer is option 3.
Solution:
$5\left(\sin \theta \cos \frac{\pi}{6}-\cos \theta \sin \frac{\pi}{6}\right)+3 \cos \theta$
$=\frac{5 \sqrt{3}}{2} \sin \theta-\frac{5}{2} \cos \theta+3 \cos \theta$
$=\frac{5 \sqrt{3}}{2} \sin \theta+\frac{1}{2} \cos \theta$
$\text { Maximum value }=\sqrt{\left(\frac{5 \sqrt{3}}{2}\right)^2+\left(\frac{1}{2}\right)^2}$
$=\sqrt{\frac{76}{4}}$
$=\sqrt{19}$
Example 5: What is the maximum value of the expression $-5 \sin (x+\pi / 4)-3 \cos (x+\pi / 4)$
1) 4
2) $4 \sqrt{2}$
3) $\sqrt{34}$
4) None of these
Solution:
Let $x+\pi / 4=\theta$
So the expression is $-5 \sin \theta-3 \cos \theta$
Its maximum value is $=\sqrt{(-5)^2+(-3)^2}=\sqrt{34}$
Hence, the answer is the option (2).
List of Topics Related to the Maximum And Minimum Value Of Trigonometric Functions
Below is the list of topics related to the maximum and minimum value of trigonometric functions for quick reference and better understanding.
NCERT Resources
Below are the NCERT resources on Trigonometric Functions, including detailed notes, solutions, and exemplar problems for effective learning and revision.
NCERT Class 11 Chapter 3 - Trigonometric Functions Notes
NCERT Class 11 solutions for Chapter 3 - Trigonometric Functions
NCERT Exemplar solutions for Class 11 Chapter 3 - Trigonometric Functions
Practice Questions on Maximum And Minimum Value Of Trigonometric Function
Below are the practice questions on maximum and minimum value of trigonometric functions to improve problem-solving skills and build strong conceptual clarity.
Maximum And Minimum Value Of Trigonometric Function - Practice Question
We have provided the list of practice questions based on the following topics:
Frequently Asked Questions (FAQs)
The maximum value of the function is M = A + |B|. This maximum value occurs whenever sin x = 1 or cos x = 1. The minimum value of the function is m = A ‐ |B|. This minimum occurs whenever sin x = −1 or cos x = −1.
To find local maximum or minimum, first, the first derivative of the function needs to be found. Values of x which makes the first derivative equal to 0 are critical points. If the second derivative at x=c is positive, then f(c) is a minimum. When the second derivative is negative at x=c, then f(c) is maximum.
Maximum value of cos θ is 1 when θ = 0 ˚, 360˚. Minimum value of cos θ is –1 when θ = 180 ˚. So, the range of values of cos θ is – 1 ≤ cos θ ≤ 1.
The max value of sinθ+cosθ=√2.