Electrical Force - Definition, Diagram, Examples, Coulomb's Law, FAQs
Have you ever asked yourself why you stick a balloon to your hair after rubbing or why there is a flash all over the sky during a thunderstorm? In fact, all of these interesting events are because of Electric Force. In this article, we will discuss what is electric force, its S.I. unit, and calculation by using Coulomb’s law, with some real-life examples.
This Story also Contains
- What is Electric Force?
- What is Coulomb’s law?
- How to Calculate Electric Force?
- Electric Force Examples
- Solved Example on Electric Force
What is Electric Force?
Electric Force Definition:
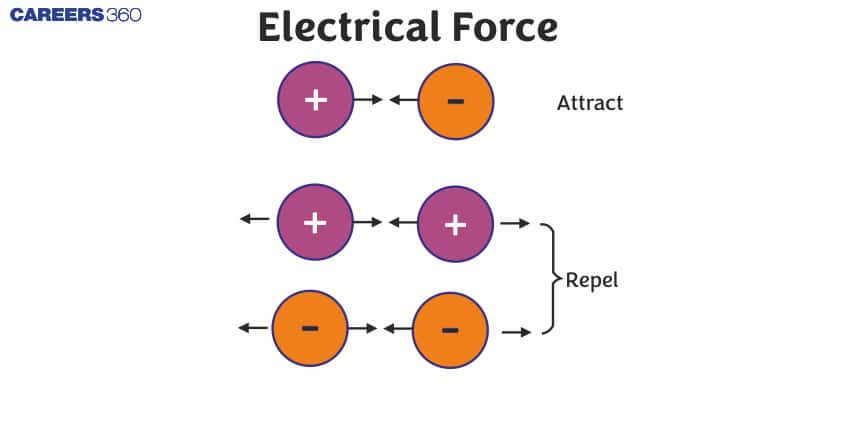
Forces that results from an interaction of electric charges that can be either attractive or repulsive is called as an Electric Force.
- Like charges (both positive or both negative) repel each other.
- Unlike Charges (one positive and one negative) attracts each other.
Simply we can say that Electric force is the force exerted between two electrically charged objects. This force is a vector quantity, meaning it has both magnitude and direction. The direction of the electric force depends on whether the charges are alike (repulsive force) or different (attractive force).
What is the S.I. Unit of Electric Force?
The SI unit of electric force is the Newton (N).
Commonly Asked Questions
What is Coulomb’s law?
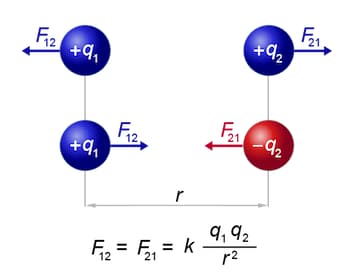
The electric force is described by Coulomb's Law, which states that the magnitude of the force $F$ between two point charges $q_1$ and $q_2$ separated by a distance $r$ is given by:
$$
F=k_e \frac{\left|q_1 q_2\right|}{r^2}
$$
where:
- $k_e$ is Coulomb's constant $\left(8.99 \times 10^9 \mathrm{~N} \mathrm{~m}^2 / \mathrm{C}^2\right)$,
- $\left|q_1 q_2\right|$ is the product of the magnitudes of the two charges,
- $r$ is the distance between the charges.
Also read -
- NCERT Exemplar Solutions for All Subjects
- NCERT Solutions for All Subjects
- NCERT Notes For All Subjects
How to Calculate Electric Force?
Electric Force is calculated by using Coulomb's law as stated above.
Steps to Calculate Electric Force:
1. Identify the charges: Determine the values of $q_1$ and $q_2$.
2. Find the distance: Find the distance $r$ between the charges.
3. Put in the values: Substitute the values of $q_1, q_2, r$, and $k_e$ into the formula.
4. Solve for $F$ : Perform the calculations to find the electric force.
Commonly Asked Questions
Electric Force Examples
The following are the electric force examples
- Static Hair Attraction: When a balloon is rubbed on hair head, then it will catch hair strands because of the formation of opposite charges.
- Lightning: When there is a difference between oppositely charged ground and cloud then there will be lightning.
- Charged Comb and Paper: Small paper pieces attracts to a comb when its is charged.
- Dust Attraction: Dust sticks to TV or computer screens due to electric charges present on their surfaces.
- Clothes Sticking Together: Clothes stick together from static electricity after drying.
What is Electrostatic Force?
Force that occurs between two charged objects that are at rest (stationary), is called as Electrostatic Force. Electrostatic Force follows Coulomb's law.
|
Related Topics |
Examples of Electrostatic Force In Our Daily Life
There are a lot of examples of electrostatic force in our daily life. Some of them are mentioned below.
- Nylon Rubbing
- Charged Comb
- Doorknob
- Woollen Clothes
- Television screen
- Photocopier
Commonly Asked Questions
Solved Example on Electric Force
Q1. Find the Electric Force between two protons.
Solution.
$$
F_e=\frac{k_e \cdot e^2}{r^2}
$$
where:
$k_e=9 \times 10^9 \mathrm{~N} \mathrm{~m}^2 / \mathrm{C}^2$
$e=1.6 \times 10^{-19} \mathrm{C}$
$r=1 \times 10^{-15} \mathrm{~m}$
1. Square the charge $e$ :
$$
e^2=\left(1.6 \times 10^{-19}\right)^2=2.56 \times 10^{-38} \mathrm{C}^2
$$
2. Square the distance $r$ :
$$
r^2=\left(1 \times 10^{-15}\right)^2=1 \times 10^{-30} \mathrm{~m}^2
$$
3. Substitute these values into Coulomb's Law:
$$
F_e=\frac{9 \times 10^9 \times 2.56 \times 10^{-38}}{1 \times 10^{-30}}
$$
4. Simplify the calculation:
$$
F_e=9 \times 10^9 \times 2.56 \times 10^{-8}
$$
5. Final calculation:
$$
F_e=230.4 \mathrm{~N}
$$
Q2. What is the magnitude of the force that a 25μC charge exerts on a −10μC charge placed at a distance of 8.5cm ?
Solution:
$$
F=k_e \frac{q_1 \cdot q_2}{r^2}
$$
where:
$k_e=9 \times 10^9 \mathrm{~N} \mathrm{~m}^2 / \mathrm{C}^2$
$q_1=+25 \mu \mathrm{C}=+25 \times 10^{-6} \mathrm{C}$
$q_2=-10 \mu \mathrm{C}=-10 \times 10^{-6} \mathrm{C}$
$r=8.5 \mathrm{~cm}=0.085 \mathrm{~m}$
1. Substitute the values:
$$
F=9 \times 10^9 \cdot \frac{\left(25 \times 10^{-6}\right) \cdot\left(-10 \times 10^{-6}\right)}{(0.085)^2}
$$
2. Calculate the product of charges:
$$
q_1 \cdot q_2=25 \times 10^{-6} \cdot\left(-10 \times 10^{-6}\right)=-2.5 \times 10^{-10} \mathrm{C}^2
$$
3. Square the distance:
$$
r^2=(0.085)^2=0.007225 \mathrm{~m}^2
$$
4. Substitute these values back:
$$
F=9 \times 10^9 \cdot \frac{-2.5 \times 10^{-10}}{0.007225}
$$
5. Calculate the division:
$$
F=9 \times 10^9 \cdot\left(-3.46 \times 10^{-8}\right)
$$
6. Final multiplication:
$$
F=-311.42 \mathrm{~N}
$$
NOTE: The negative sign in the electric force indicates that the forces between the given two-particle are attractive in nature.
Frequently Asked Questions (FAQs)
