Unit of Electric Flux - Definition, Formula, FAQS
In this article we are going to learn about Electric flux, S.I unit of electric flux, Electric flux density , Unit of electric flux density and many more.
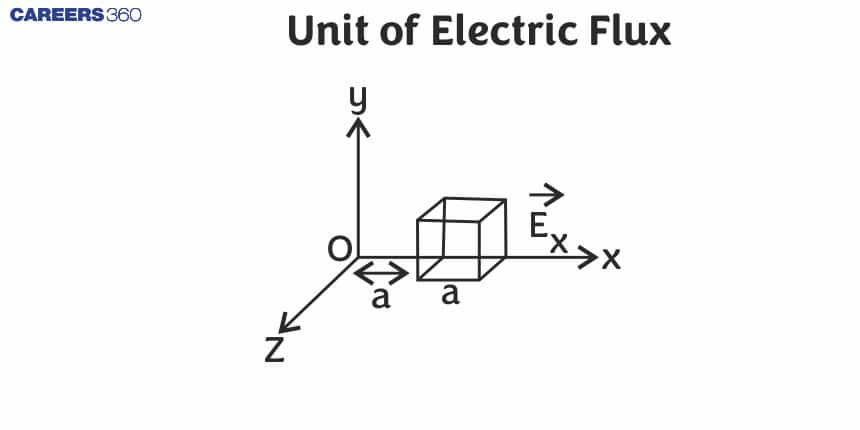
What is Electric Flux?
An electric field's property is electric flux.
It can be compared to the number of forces that cross a certain area.
Electric field lines are commonly thought to begin with positive charges and conclude with negative charges.
Negative field lines are those that are directed into a closed surface, whereas positive field lines are those that are directed out of a closed surface.
If no net charge exists within a closed surface, every field line directed into the surface passes through the interior and is usually directed outward elsewhere on the surface.
The negative flux just equals the positive flux in magnitude, resulting in a net or total electric flow of zero.
When a net charge is imprisoned inside a closed surface, the total flux through the surface is proportional to the enclosed charge, positive if the charge is positive and negative if the charge is negative.
Also read -
- NCERT Solutions for Class 11 Physics
- NCERT Solutions for Class 12 Physics
- NCERT Solutions for All Subjects
JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide
JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days
NEET 2025: Syllabus | High Scoring Topics | PYQs
Gauss law
Gauss law for the electric field is the mathematical relationship between electric flux and the contained charge.
It's one of electromagnetism's fundamental rules.
The net flux of an electric field through any closed surface is usually equal to the enclosed charge, in coulombs, divided by a constant termed the permittivity of free space in the related meter-kilogram-second system and the International System of Units (SI).
The net flow of an electric field through any closed surface in the centimetre-gram-second system is equal to 4 times the contained charge, measured in electrostatic units (esu).
The number of electric field lines passing through a virtual surface determines the electric flux.
This can be explained using an equation.
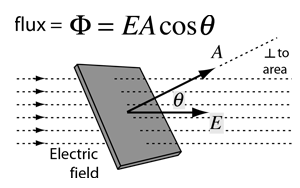
The electric flux (ΦE)) travelling through a surface of vector area S if the electric field is homogeneous is:
ΦE = E⋅S = EScosθ,
where E is the electric field's magnitude (in units of V/m), S is the surface's area and is the angle between the electric field lines and the normal (perpendicular) to S.
The electric flux dΦE through a small surface area dS in a non-uniform electric field is commonly indicated by:
dΦE=E⋅dS,
where E denotes the electric field, and A denotes the area component perpendicular to the field.
SI unit of electric flux
Voltmeters (V m), which is also equivalent to newton-meters squared per coulomb, are the SI base unit of electric flux (N m2 C-1)
Furthermore, kg·m3·s-3·A-1.is the fundamental unit of electric flux.
We now know that (N m2 C-1) is the SI unit for electric flux.
M = MASS.
L = LENGTH.
T = TIME.
I = CURRENT
Related Topics Link, |
As a result, we know that the SI unit of force ‘N/Newton' is represented in dimension as MLT−2
M 2 represents the SI unit of meter
Length is represented in dimension as L2 .
And ‘C’ the SI unit of charge is represented in dimension as M0 L 0 T 1 I 1 ,
As a result, the dimensional values are converted to the SI unit of electric flux. (N m2 C-1) we get, M·L3·T-3·I-1
Electric flux dimensional formula
Electric flux is a measure of the dispersion of the electric field through a specific surface in electromagnetism.
The electric flux dimensional formula is discussed earlier
[M L3 T−3 A−1]
Also Read:
- NCERT solutions for Class 12 Physics Chapter 1 Electric Charges and Fields
- NCERT Exemplar Class 12 Physics Solutions Chapter 1 Electric Charges and Fields
- NCERT notes Class 12 Physics Chapter 1 Electric Charges and Fields
Electric flux density
Electric flux density is the electric flux passing through a unit area perpendicular to the direction of the flux. Electric flux density is a measure of the strength of an electric field generated by a free electric charge.
Unit of electric flux density
Electric flux density is obtained by flux passing per unit area.
Unit of ϕ=Nm2/C
Unit of electric flux density=Nm2/C/m2=N/C
Conclusion
Electric flux is a scalar quantity
The SI unit of electric flux is (N m2 C-1)
The dimensional formula of electric flux is M·L3·T-3·I-1
Also, check-
- NCERT Exemplar Class 11th Physics Solutions
- NCERT Exemplar Class 12th Physics Solutions
- NCERT Exemplar Solutions for All Subjects
NCERT Physics Notes:
Frequently Asked Questions (FAQs)
Voltmeters (V m), which is also equivalent to newton-meters squared per coulomb, are the SI base unit of electric flux (N m2 C-1)
kg·m3·s-3·A-1.is the fundamental unit of electric flux.
An electric field's property is electric flux.
It can be compared to the number of forces that cross a certain area.
Electric field lines are commonly thought to begin with positive charges and conclude with negative charges.
Negative field lines are those that are directed into a closed surface, whereas positive field lines are those that are directed out of a closed surface.
If no net charge exists within a closed surface, every field line directed into the surface passes through the interior and is usually directed outward elsewhere on the surface.
The negative flux just equals the positive flux in magnitude, resulting in a net or total electric flow of zero.
When a net charge is imprisoned inside a closed surface, the total flux through the surface is proportional to the enclosed charge, positive if the charge is positive and negative if the charge is negative.
SI unit of electric flux (N m2 C-1)
Dimensional formula of electric flux
We now know that (N m2 C-1) is the SI unit for electric flux.
M = MASS.
L = LENGTH.
T = TIME.
I = CURRENT
[M L3 T−3 A−1] is the dimension of electric flux.
Electric flux density
Electric flux density is the electric flux passing through a unit area perpendicular to the direction of the flux. Electric flux density is a measure of the strength of an electric field generated by a free electric charge.
Unit of electric flux density
Electric flux density is obtained by flux passing per unit area.
Unit of electric flux density=N/C
Yes it is a scalar quantity
When the surface is perpendicular to the field.
The flux lines are directed outwards when the flux lines are directed outwards.
Also Read
14 Nov'24 02:18 PM
14 Nov'24 01:05 PM
14 Nov'24 12:05 PM
14 Nov'24 10:56 AM
12 Nov'24 10:01 PM
12 Nov'24 07:54 PM
11 Nov'24 02:05 PM
24 Sep'24 04:48 PM