Superposition Principle and Continuous Charge Distribution

Superposition Principle and Continuous Charge Distribution - Detailed Guide

Edited By Team Careers360 | Updated on Jul 02, 2025 05:04 PM IST

In this article, we will learn about the law of superposition which is also known as the principle of superposition.
Note: Superposition theorem in hindi is अध्यारोपण प्रमेय

What is superposition?/superposition meaning:

Overlapping one thing over the other is called the superposition.

Also read -

Superposition Principle and Continuous Charge Distribution - Detailed Guide

What is principle of superposition?/superposition principle in electrostatics/define principle of superposition

The principle of superposition states that the total force on a charge due to a number of other charges is given by the vector sum of the Coulomb forces exerted on the charge due to each of the other charges acting separately. This law is also known as the principle of superposition of forces.

Let us consider , there are N no of point charges like q1,q2,q3,q4,…….,qN.The total force acting on charge q for N no of charges is the sum of the individual forces F1,F2,F3,F4…..FN .So, the total force on the charge q is

F=F1+F2+F3+F4+…+FN=i=1NFi

The superposition principle is used in the calculation field, flux, potential energy of an electrostatic system.

Let us consider an example,

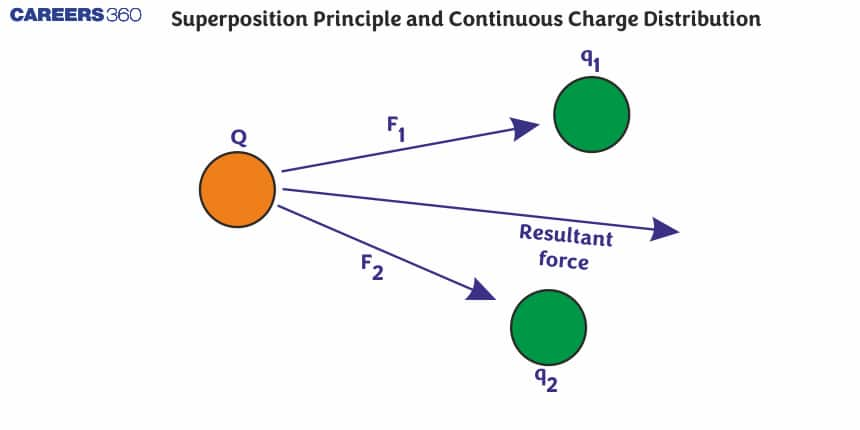
According to Coulomb’s law, the force between two charges be,

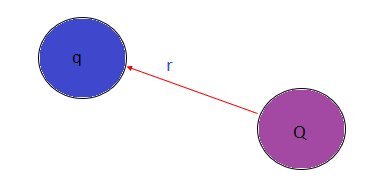
According to Coulomb’s law, the force between two charges

F=14π0.Q.qr2.r

Here,

F = total force

Q = test charge

q = point charge

r = distance between two charges

The principle of superposition can be shown with a minimum of three charges, but this principle is used for a large number of charges or N number of charges. In the below example, we will discuss the superposition principle

superposition principle

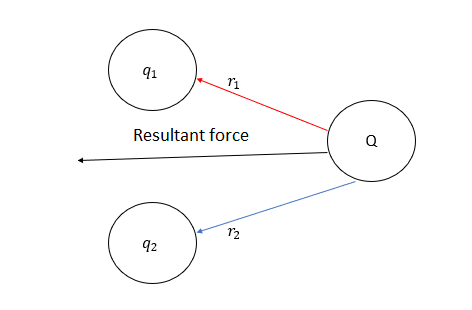
According to the diagram,

F1=14π0Q.q1r12r1

F2=14π0Q.q2r22r2

According to the principle of superposition

FQ=14π0[Q.q1r12+Q.q2r22]r

Here , Q = test charge ; q1=q2= point charge; r1= distance between the test charge and q1 charge ; r2= distance between the test charge and q2 charge ;r = the direction of the resultant force ; FQ= resultant force .

Related Topics Link,

Continuous charge distribution:

As we know, charge carried by a body is always an integral multiple of the smallest unit of charge which is a charge of an electron. According to this theory of quantisation of charge, it can be said that an electron has the smallest charge.

When the charges are very closely bound to each other then that type of charge distribution is known as continuous charge distribution.

According to the principle of superposition of charges, here are three types of continuous charge

linear charge distribution
Surface charge distribution
Volume charge distribution

Also Read:

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

1. Linear charge distribution:

When the charges are distributed uniformly in one dimension or along length then this type of charge distribution is known as linear charge distribution.

2. Surface charge distribution :

When the charges are distributed uniformly in two dimensions or along a surface then this type of charge distribution is known as surface charge distribution.

3. Volume charge distribution :

When the charges are distributed uniformly in three dimensions or along a volume then this type of distribution is known as volume charge distribution.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What are the applications of problems on the principle of superposition?

They help to determine the equations in Physics like heat equations etc. So, they use it to solve the linear differential equations.

2. What is the unit of charge density?

Unit of charge density is Coulomb per square meters or C/m2.

3. What is Gauss’s law?

The flux of the electric field through any closed surface is equal to the net charge divided by the permittivity of free space.

4. Define volume charge density and write its unit.

Volume charge density is the continuous charge distribution over the volume. Unit of volume charge density is cm3.

5. Define neutral charge.

In an atom, if the number of protons and electrons are equal then it is called neutral charge.

6. What is the SI unit of charge?

Coulomb is the unit of charge.

7. What are cations and anions?

Cations are positively charged ions and anions are negatively charged ions.

8. Define electric flux.

Electric flux is the measure of number of electric field lines that pass through any surface.

9. How does the superposition principle apply to continuous charge distributions?

For continuous charge distributions, the superposition principle is applied by dividing the distribution into infinitesimal charge elements. The total electric field is then calculated by integrating the contributions from all these elements over the entire distribution. This approach allows us to handle charge distributions that are not discrete points but spread out in space.

10. What is a continuous charge distribution?

A continuous charge distribution is an arrangement of electric charge that is spread out continuously over a region of space, rather than existing as discrete point charges. Examples include charged surfaces, lines, or volumes where the charge density may vary smoothly across the distribution.

11. How do we mathematically represent charge density in continuous distributions?

Charge density in continuous distributions is represented using three main quantities:

12. Why is it necessary to use calculus when dealing with continuous charge distributions?

Calculus is necessary because continuous charge distributions involve infinitesimal charge elements that contribute to the overall electric field. Integration allows us to sum up these infinitesimal contributions over the entire distribution, providing an exact result for the total electric field or potential.

13. What is the difference between discrete and continuous charge distributions?

Discrete charge distributions consist of individual point charges at specific locations, while continuous charge distributions have charge spread out smoothly over a region of space. Discrete distributions are summed, while continuous distributions require integration to calculate their effects.

14. What is the superposition principle in electrostatics?

The superposition principle in electrostatics states that the total electric field at any point due to multiple charges is the vector sum of the individual electric fields produced by each charge. This principle allows us to calculate the net electric field in complex charge distributions by breaking them down into simpler components and adding their effects.

15. Can the superposition principle be applied to both electric fields and electric potentials?

Yes, the superposition principle applies to both electric fields and electric potentials. The total electric field is the vector sum of individual fields, while the total electric potential is the scalar sum of individual potentials from all charge elements in the distribution.

16. What are the limitations of the superposition principle in electrostatics?

The superposition principle in electrostatics assumes that the charges are stationary and do not influence each other's positions. It may not apply directly to systems with moving charges or where charges can redistribute themselves in response to external fields.

17. What is the significance of Coulomb's law in applying the superposition principle?

Coulomb's law forms the basis for applying the superposition principle. It describes the electric field or force due to a single point charge, which is then used as the building block for calculating fields from multiple charges or continuous distributions through superposition.

18. How does one determine whether to use discrete summation or integration when applying the superposition principle?

The choice between discrete summation and integration depends on the nature of the charge distribution. If the charges are distinct and countable, use summation. If the charge is continuously distributed over a region, use integration. Sometimes, a combination of both methods may be necessary for complex systems.

19. How does the superposition principle help in understanding the concept of electric field energy density?

The superposition principle allows us to calculate the total electric field at any point, which is crucial for determining the electric field energy density. The energy density is proportional to the square of the electric field magnitude, which is found by superposing the fields from all charge sources.

20. What is the significance of the superposition principle in understanding the behavior of dielectrics in electric fields?

The superposition principle helps explain the behavior of dielectrics by allowing us to consider the combined effect of the external electric field and the field produced by the aligned dipoles within the dielectric. This superposition results in the observed reduction of the electric field inside the dielectric.

21. How does the superposition principle apply to the concept of electric field lines crossing?

The superposition principle shows that electric field lines from different sources can intersect. At any point, the resultant electric field is the vector sum of the fields from all sources. This means that while field lines from a single source don't cross, the superposed field lines from multiple sources can intersect.

22. What is the relationship between the superposition principle and the work done in moving a charge in an electric field?

The superposition principle allows us to calculate the total electric field, which is essential for determining the work done in moving a charge. The work is calculated using the total field, which is the superposition of fields from all charges, integrated along the path of the moving charge.

23. What is the importance of vector addition in applying the superposition principle to electric fields?

Vector addition is crucial in applying the superposition principle to electric fields because electric fields are vector quantities. The direction of the field is as important as its magnitude. Proper vector addition ensures that the resulting field accurately represents the combined effect of all charge sources.

24. How does the concept of charge density relate to the superposition principle?

Charge density allows us to describe how charge is distributed in a continuous system. When applying the superposition principle to continuous distributions, we use charge density to determine the contribution of each infinitesimal element to the total electric field or potential, then integrate these contributions.

25. How does the shape of a charge distribution affect the application of the superposition principle?

The shape of the charge distribution determines how we set up the integration for applying the superposition principle. Different shapes (e.g., linear, planar, or volumetric) require different coordinate systems and integration limits to properly sum the contributions from all charge elements.

26. What is the key difference in applying superposition to symmetric vs. asymmetric charge distributions?

For symmetric charge distributions, we can often simplify calculations by exploiting symmetry to reduce the complexity of the integration. Asymmetric distributions generally require more complex integration over the entire charge distribution without such simplifications.

27. How does the distance from a continuous charge distribution affect the electric field calculation?

The distance from a continuous charge distribution affects both the magnitude and complexity of the electric field calculation. At large distances, many continuous distributions can be approximated as point charges, simplifying calculations. At closer distances, the full integration over the distribution is necessary for accurate results.

28. What is the importance of choosing the right coordinate system when dealing with continuous charge distributions?

Choosing the right coordinate system (Cartesian, cylindrical, or spherical) can greatly simplify the integration process when applying the superposition principle to continuous charge distributions. The appropriate choice depends on the symmetry and geometry of the charge distribution.

29. How does Gauss's law relate to the superposition principle for continuous charge distributions?

Gauss's law is an alternative approach to the superposition principle for calculating electric fields from continuous charge distributions. It relates the flux of the electric field through a closed surface to the enclosed charge, and can simplify calculations for highly symmetric charge distributions.

30. What is the significance of the infinitesimal charge element dq in continuous charge distribution calculations?

The infinitesimal charge element dq represents a tiny portion of the total charge in a continuous distribution. It is crucial for setting up the integral to apply the superposition principle, as it allows us to sum up the contributions from all parts of the distribution to find the total electric field or potential.

31. How does one handle a continuous charge distribution with varying charge density?

For a continuous charge distribution with varying charge density, the charge density function must be incorporated into the integration. The infinitesimal charge element dq is expressed in terms of the charge density function and the appropriate differential element (length, area, or volume) before integration.

32. What is the relationship between electric field lines and the superposition principle?

Electric field lines provide a visual representation of the electric field. When applying the superposition principle, the resulting electric field lines are a combination of the field lines from individual charges or charge elements. The principle helps explain how field lines from multiple sources interact and combine.

33. How does the concept of electric flux relate to continuous charge distributions?

Electric flux is the flow of the electric field through a surface. For continuous charge distributions, the flux can be calculated by integrating the electric field over the surface. This concept is particularly useful in applying Gauss's law to find the electric field of symmetric charge distributions.

34. What role does the principle of superposition play in understanding the behavior of conductors in electrostatic equilibrium?

The superposition principle helps explain how charges redistribute on a conductor to achieve electrostatic equilibrium. The net electric field inside a conductor must be zero, which is achieved by the superposition of fields from all charges, including those induced on the conductor's surface.

35. How does one apply the superposition principle to calculate the electric potential from a continuous charge distribution?

To calculate the electric potential from a continuous charge distribution, we integrate the contributions to the potential from each infinitesimal charge element dq over the entire distribution. This is similar to the electric field calculation but involves scalar addition rather than vector addition.

36. What is the significance of the 1/r² dependence in Coulomb's law when applying superposition to continuous distributions?

The 1/r² dependence in Coulomb's law is crucial when integrating over continuous distributions. It determines how the contribution from each charge element scales with distance, often leading to interesting results where closer parts of the distribution contribute more significantly to the field or potential.

37. How does the principle of superposition help in understanding the concept of electric dipoles?

The principle of superposition allows us to understand electric dipoles as the combined effect of two equal and opposite charges. The electric field and potential of a dipole can be calculated by superposing the contributions from the positive and negative charges, leading to characteristic dipole fields.

38. What is the importance of understanding superposition in the context of electrostatic shielding?

Superposition is key to understanding electrostatic shielding. The principle explains how the fields from induced charges on a conductor can cancel external fields inside the conductor, creating a field-free region. This concept is fundamental to the operation of Faraday cages and other shielding devices.

39. How does the superposition principle apply to systems with both discrete charges and continuous distributions?

In systems with both discrete charges and continuous distributions, the superposition principle allows us to calculate the total electric field or potential by adding the contributions from the discrete charges to the integrated contributions from the continuous distributions.

40. What is the relationship between the superposition principle and the linearity of Maxwell's equations in electrostatics?

The superposition principle is a direct consequence of the linearity of Maxwell's equations in electrostatics. This linearity means that the equations governing electric fields and potentials are additive, allowing us to combine solutions for complex charge distributions from simpler ones.

41. How does one apply the superposition principle to calculate the force on a test charge in a complex electric field?

To calculate the force on a test charge in a complex electric field, first use the superposition principle to determine the total electric field at the test charge's location by summing contributions from all sources. Then, multiply this field by the test charge to find the force using F = qE.

42. What are some common misconceptions about the superposition principle in electrostatics?

Common misconceptions include:

43. How does the concept of superposition relate to the method of images in electrostatics?

The method of images uses the superposition principle to simplify problems involving conductors. It replaces a complex system of a charge and a conductor with an equivalent system of charges in free space. The principle allows the fields from the real and image charges to be superposed to satisfy boundary conditions.

44. What is the significance of the superposition principle in understanding the electric field inside a conductor?

The superposition principle explains why the electric field inside a conductor in electrostatic equilibrium is zero. The fields from all charges, including those induced on the surface, superpose to cancel each other out within the conductor. This principle is crucial for understanding charge distribution on conductors.

45. How does one apply the superposition principle to calculate the electric field from a non-uniform line charge?

For a non-uniform line charge, divide the line into infinitesimal segments, each with charge dq = λ(x)dx, where λ(x) is the varying linear charge density. Calculate the field contribution from each segment using Coulomb's law, then integrate these contributions over the entire line to find the total field.

46. What is the role of symmetry in simplifying calculations when applying the superposition principle?

Symmetry can greatly simplify calculations when applying the superposition principle. For symmetric charge distributions, the field contributions from symmetric elements may cancel in certain directions, reducing the complexity of the integration or allowing the use of Gauss's law instead of direct integration.

47. How does one apply the superposition principle to calculate the electric field from a charged ring?

To calculate the electric field from a charged ring, divide the ring into infinitesimal segments. Calculate the field contribution from each segment using Coulomb's law, considering its distance and orientation relative to the point of interest. Integrate these contributions around the entire ring to find the total field.

48. How does one apply the superposition principle to calculate the electric potential from a charged disk?

To calculate the electric potential from a charged disk, divide the disk into concentric ring elements. Calculate the potential contribution from each ring element and integrate these contributions over the entire disk radius. The superposition principle allows us to sum these infinitesimal contributions to find the total potential.

49. What is the significance of the superposition principle in understanding the concept of capacitance?

The superposition principle is crucial in understanding capacitance as it allows us to calculate the total electric field and potential between capacitor plates. This is essential for determining the charge distribution on the plates and the energy stored in the capacitor, which define its capacitance.

50. How does the superposition principle help in analyzing the electric field near the edge of a charged conductor?

Near the edge of a charged conductor, the superposition principle allows us to consider the combined effect of charges distributed over the conductor's surface. This explains the stronger electric fields observed near edges and points, as the superposed fields from different parts of the conductor add up more intensely in these regions.

51. What is the role of the superposition principle in understanding the concept of electric field screening?

The superposition principle is key to understanding electric field screening. It explains how the fields from induced charges (e.g., in a conductor or plasma) can partially or fully cancel an external electric field. The net field is the superposition of the external field and the field from the induced charges.

52. How does one apply the superposition principle to calculate the electric field from a uniformly charged sphere?

For a uniformly charged sphere, divide it into concentric spherical shells. Calculate the field contribution from each shell using Gauss's law (which is based on superposition). Integrate these contributions from the center to the surface for points inside the sphere, or use the total charge as a point source for points outside.

53. What is the importance of understanding superposition in the context of electrostatic boundary value problems?

Superposition is crucial in solving electrostatic boundary value problems. It allows complex problems to be broken down into simpler ones whose solutions can be added. This principle is the basis for techniques like the method of images and separation of variables used in solving these problems.

54. How does the superposition principle apply to the concept of electric field gradient?

The electric field gradient, which describes how the electric field changes in space, also follows the superposition principle. The total field gradient at any point is the vector sum of the gradients from all charge sources, allowing us to analyze complex field variations in multi-charge systems.

55. What is the significance of the superposition principle in understanding the behavior of electric multipoles?

The superposition principle is fundamental to understanding electric multipoles (dipoles, quadrupoles, etc.). These are analyzed as combinations of point charges whose fields superpose. The principle explains how the fields from these charge arrangements combine to produce characteristic multipole fields at different distances.

56. How does one apply the superposition principle to analyze the electric field inside a hollow conductor?

The superposition principle explains why the electric field inside a hollow conductor is zero. The fields from charges on the outer surface and any induced charges on the inner surface superpose to cancel each other out completely within the hollow region, regardless of external fields.

57. What is the role of the superposition principle in understanding the concept of electrostatic induction?

Electrostatic induction is understood through the superposition principle. The total electric field in and around an induced conductor is the superposition of the external field and the field from the induced charges. This principle explains how the induced charges arrange themselves to make the field inside the conductor zero.

58. How does the superposition principle help in analyzing complex systems of conductors and dielectrics in electrostatics?

In complex systems of conductors and dielectrics, the superposition principle allows us to break down the problem into simpler parts. We can analyze the effects of each conductor and dielectric separately, then superpose their contributions to understand the overall electric field and potential distribution in the system