Gravitation - Notes, Topics, Formulas, Books, FAQs
Gravitation is a basic chapter in the Class 11 Physics syllabus, which is concerned with the universal force of attraction between masses. This chapter teaches the students about the role of a gravitational interaction in the movement of celestial bodies and the objects that are close to the Earth. Physics describes a phenomenon of the gravitational properties based on the well-established laws that assist in studying the motions both on Earth and in space.
This Story also Contains
- Important Topics of Gravitation
- Important Formulas of Gravitation
- Gravitation: Previous Year Questions
- Gravitation in Different Exams
- Important Books and Resources for Class 11 Gravitation
- NCERT Resources for Gravitation
- NCERT Subject-Wise Resources
- Practice Questions based on Gravitation
- Conclusion
.jpg)
In order to examine the concept of gravitation well, there is a need to establish clear definitions of the gravitational force, the gravitational constant, the acceleration due to gravity, mass, weight and distance. It is insufficient to state that the object moves under the influence of gravity unless the forces and their dependence on the mass and distance are mentioned. Equally, the study of gravitational interactions cannot be undertaken without the introduction of relationships between force, mass, distance and energy. The gravitational effects can be studied with accuracy and consistency through the use of the standard definitions and well-established equations. Moreover, the chapter also mentions the key notions of Newton's law of gravitation, acceleration due to gravity variation, gravitational potential and potential energy, escape velocity, orbital motion, and laws of Kepler. It emphasises the use of experimental observations in these principles and describes their use in a wide variety of physical cases, starting with falling bodies through to the motion of planets. The study of gravitation will also allow students to connect theoretical concepts to real-world phenomena and give them a solid background in more complicated subjects in mechanics and astrophysics.
Important Topics of Gravitation
The important topics of the chapter Gravitation explain the nature and effects of the gravitational force acting between masses. The topics provide the following fundamental concepts: the gravitational attraction, gravitational field, energy of gravity and motion due to the influence of gravity. They assist students in knowing how the concept of gravity controls such occurrences on Earth and also planetary and satellite motions. Mastery of the topics is critical in solving numerical problems and in building a powerful conceptual base in mechanics.
1. Newton’s Law of Gravitation
According to the law of gravitation, any two masses in the universe have a force of attraction directly proportional to the product of their masses and inversely proportional to the square of the distance between the centres of the masses. This law describes gravitational attraction among heavenly bodies and objects on Earth. It is universal and is applicable to all masses regardless of their size. This law is the pillar of gravitational studies.
2. Acceleration Due to Gravity
Acceleration due to gravity (g) represents the acceleration experienced by a body because of the gravitational attraction of the Earth. Close to the surface of the earth, its average value is 9.8 ms-2. It does not depend on the mass of the falling object, as can be seen through experimental observations. The idea of g assists in explaining the free fall and vertical motion under the influence of gravity. It is significant in getting answers to numerical problems involving motion.
3. Variation of Acceleration Due to Gravity
The acceleration due to gravity depends on the height above the surface of the earth, the depth below the surface and latitude. The value of g decreases with height or depth. g is a maximum at the poles and a minimum at the equator because of earth rotation and shape. These variations denote the variation in weight at various places. Conceptual and numerical questions on this topic are often asked.
4. Mass and Weight
Mass represents the quantity of matter that is present in a body, and it does not change anywhere. W is the gravitational force exerted on a body, which is equal to wW=mg. Weight also depends on location, unlike mass, as the value of g varies. This difference states the reason astronauts experience weightlessness in space, but their mass does not change. To understand problems about gravitation, it is necessary to understand mass and weight.
5. Gravitational Potential
Gravitational potential at a point is the effect of a gravitational field in performing work on a unit mass. It aids in explaining the strength with which a mass is drawn at various positions in a gravitational field. Gravitational potential is dependent on the position with respect to the attracting body, and it decreases with the increase in the distance from the body. The concept can be applied to the study of gravitational fields and variations in energy.
6. Gravitational Potential Energy
Gravitational potential energy is the energy possessed by a body due to its position in a gravitational field. The energy which a body has because it is in a gravitational field is called gravitational potential energy. It occurs since one works against gravity as one lifts a body. When free motion of the body under gravity is possible, this energy can be converted into kinetic energy. The concept is significant in the explanation of energy conservation as well as motion under gravity.
7. Escape Velocity
Escape velocity is the lowest possible speed that an object must have to overcome the attraction of a planet or other celestial body due to the gravitational force. An object moving at such speed will be able to move away forever without returning. The escape velocity is not proportional to the mass of the escaping body, but to the gravitational strength of the body. The idea is core to the exploration of space and launching satellites.
8. Orbital Velocity
Orbital velocity refers to the velocity needed by an object to orbit a planet in a circular orbit. At this velocity, the centripetal force required to cause circular motion is given by the gravitational force. Orbital velocity enables satellites to be in a continuous free fall around the Earth. It plays a significant role in the explanation of the movement of natural and artificial satellites.
9. Motion of Satellites
The gravitational force that acts as the centripetal force controls the motion of satellites. The planets orbit around each other in circular or elliptical orbits. Communication, weather forecasting, navigation and scientific research are all done with the help of artificial satellites. The knowledge of the satellite motion assists in the explanation of geostationary and polar orbits. This topic connects gravitation with real-life applications.
10. Kepler’s Laws of Planetary Motion
Kepler's laws describe the motion of planets around the Sun. The first law states that planets move in elliptical orbits with the Sun at one focus. The second law explains that a planet sweeps equal areas in equal intervals of time. The third law establishes a relation between the square of the time period and the cube of the semi-major axis of the orbit. These laws support Newton’s law of gravitation.
Important Formulas of Gravitation
1. Universal Law of Gravitation:
$
F=G \frac{m_1 m_2}{r^2}
$
$F=$ Gravitational force, $m_1, m_2=$ masses, $r=$ distance
2. Acceleration due to Gravity on Earth:
$
g=\frac{G M}{R^2}
$
$M=$ Mass of Earth,$R=$ Radius of Earth, $G=$ Gravitational constant
3. Weight of a Body:
W = mg
4. Variation of Acceleration Due to Gravity:
- With height $h$ :
$
g_h=g\left(1-\frac{2 h}{R}\right)
$
- With depth $d$ :
$
g_d=g\left(1-\frac{d}{R}\right)
$
5. Gravitational Potential:
$V=-\frac{G M}{r}$
6. Gravitational Potential Energy:
- Near Earth's surface:
$
U=m g h
$
- At distance $r$ :
$
U=-\frac{G M m}{r}
$
7. Escape Velocity:
$v_e=\sqrt{\frac{2 G M}{R}}$
8. Orbital Velocity:
$v_o=\sqrt{\frac{G M}{R}}$
9. Relation Between Escape and Orbital Velocity:
$v_e=\sqrt{2} v_o$
10. Time Period of a Satellite:
$T=2 \pi \sqrt{\frac{r^3}{G M}}$
11. Kepler’s Third Law:
$T^2 \propto r^3$
Gravitation: Previous Year Questions
The past-year questions in the chapter Gravitation are primarily concerned with the use of Newton's law of gravitation, change of acceleration due to gravity, gravitational potential and potential energy, as well as satellite motion. These questions make students become aware of the pattern of the exam and know the common concepts and formulas that the students will be assessed on. Their practice enhances the ability to solve numerical problems and conceptual clarity. This part is very helpful in efficient revision and examination preparation.
Question 1:
The value of acceleration due to gravity at a height of 10 km from the surface of the Earth is x. At what depth inside the earth is the value of the acceleration due to gravity having the same value as x?
Solution:
According to the question -
$
g_d=g_o\left(1-\frac{d}{R}\right)=g_h=g_0\left(1-\frac{2 h}{R}\right)
$
So,
$
g_o\left(1-\frac{d}{R}\right)=g_0\left(1-\frac{2 h}{R}\right)
$
So,
$
d=2 h
$
h = 10 km (given)
so,
d = 20 km
Question 2:
Two satellites $S_1$ and $S_2$ are revolving around a planet in the opposite sense in coplanar circular concentric orbits. At time $t=0$, the satellites are farthest apart. The periods of revolution of $S_1$ and $S_2$ are 3 h and 24 h, respectively. The radius of the orbit of $S 1$ is $3 \times 10^4 \mathrm{~km}$. Then the orbital speed of $S_2$ as observed from
(A) the planet is $4 \pi \times 10^4 \mathrm{~km} \mathrm{~h}^{-1}$ when $S_2$ is closest from $S_1$.
(B) the planet is $2 \pi \times 10^4 \mathrm{~km} \mathrm{~h}^{-1}$ when $\mathrm{S}_2$ is closest from $\mathrm{S}_1$.
(C) $S_1$ is $\pi \times 10^4 \mathrm{~km} \mathrm{~h}^{-1}$ when $S_2$ is closest from $S_1$
(D) $S_1$ is $3 \pi \times 10^4 \mathrm{~km} \mathrm{~h}^{-1}$ when $S_2$ is closest from $S_1$
Solution:
From Kepler's Laws,
$
\begin{aligned}
& \frac{\mathrm{R}_1^3}{\mathrm{R}_2^3}=\frac{\mathrm{T}_1^2}{\mathrm{~T}_2^2} \\
& \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{1}{4} \\
& \mathrm{R}_2=12 \times 10^4 \mathrm{~km}
\end{aligned}
$
Relative to the planet,
$
\begin{aligned}
& \mathrm{v}_1=\frac{2 \pi \mathrm{R}_1}{\mathrm{~T}_1}=\frac{2 \pi \times 3 \times 10^4}{3}=2 \pi \times 10^4 \mathrm{~km} / \mathrm{h} \\
& \mathrm{v}_2=\frac{2 \pi \mathrm{R}_2}{\mathrm{~T}_2}=\frac{2 \pi \times 12 \times 10^4}{24}=\pi \times 10^4 \mathrm{~km} / \mathrm{h}
\end{aligned}
$
At the closest approach distance between $S_1 \& S_2$, the relative orbital speed of $\mathrm{S}_2$ as seen from $S_1$ will be $v_1+v_2$ as they are moving in opposite directions. Hence, the above orbital speed is:
$
\mathrm{v}=\mathrm{v}_1+\mathrm{v}_2=3 \pi \times 10^4 \mathrm{~km} / \mathrm{hr}
$
Hence, the answer is option (D).
Question 3:
A comet (assumed to be in an elliptical orbit around the sun) is at a distance of 0.4 AU from the sun at the perihelion. If the time period of the comet is 125 years, what is the aphelion distance? AU: Astronomical Unit.
Solution:
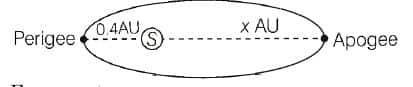
For a comet, the mean orbital radius,
$
r_1=\frac{0.4+x}{2} A U
$
Now, using $T^2 \propto r^3$, we get
$
\left(\frac{T_1}{T_2}\right)^2=\left(\frac{r_1}{r_2}\right)^3 \ldots
$
Let $T_2$ and $r_2$ are time period and mean orbital radius for Earth.
Then, $T_2=1 y r$ and $r_2=1 A U$ Also given,
$
T_1=125 \mathrm{yr}
$
Substituting values in Eq. (i), we get
$
\begin{aligned}
& \left(\frac{125}{1}\right)^2=\left(\frac{0.4+x}{2(1)}\right)^3 \\
& \Rightarrow(0.4+x)^3=(125)^2\left(2^3\right) \\
& \Rightarrow(0.4+x)^3=\left(5^6\right)\left(2^3\right) \\
& \Rightarrow 0.4+x=\left(5^2\right)(2) \\
& \Rightarrow x=50-0.4=49.6 A U
\end{aligned}
$
Gravitation in Different Exams
The chapter Gravitation is an important and scoring topic across various school-level and competitive examinations due to its strong conceptual base and wide range of applications. This chapter is examined in different examinations in the form of numerical problems, conceptual questions, and real life application related to the motion of planets and satellites. A good knowledge of the laws of gravity, the concept of energy and the movement under the influence of gravity will enable students to deal with the questions of different complexity.
| Exam | Focus Areas | Common Questions Asked | Marks / Questions Weightage | Preparation Tips |
|---|---|---|---|---|
| JEE Main | Newton’s law, satellites, escape & orbital velocity | Numerical MCQs, formula-based problems | 1–2 questions (4–8 marks) | Strong grip on formulas, practice numericals |
| JEE Advanced | Central force motion, gravitation & energy | Conceptual + multi-step numerical problems | 1 question (variable marks) | Focus on derivations and deep concepts |
| NEET | Gravitation basics, satellites, (g) variation | Direct NCERT-based MCQs | 1–2 questions (4–8 marks) | Memorise formulas and NCERT examples |
| UPSC CDS / NDA | Basics of gravitation | One-liners, simple numericals | 1 question (2–4 marks) | Revise definitions and standard results |
| State-Level Exams (WBJEE, MHT-CET, etc.) | Gravitation & satellite motion | Conceptual + numerical MCQs | 1–2 questions (4–8 marks) | Practice PYQs and speed-based problems |
| GATE | Gravitation fundamentals | Conceptual questions (limited) | Low/rare | Focus on core principles |
| School-Level (CBSE, ICSE, State Boards) | Entire chapter | Numericals, derivations | 6–8 marks | Master NCERT theory and derivations |
| CUET | Conceptual understanding | MCQs, assertion–reason | 1–2 questions (4–6 marks) | Focus on gravitation concepts |
| SSC & Banking Exams | Basic gravitation facts | One-liners, matching type | 1 question (1–2 marks) | Revise applications and definitions |
Important Books and Resources for Class 11 Gravitation
In order to master the chapter Gravitation, students are advised to make use of good-quality textbooks, reference guides, and practice materials that perfectly elaborate on the concepts of gravitation, laws, motion under gravity, and satellite motion. These materials assist in developing good concept clarity and numerical skills for solving numbers required in school exams and also competitive exams such as the JEE Main, the JEE Advanced exams, NEET exams and other entrance exams.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Class 11 Physics (Part I) | NCERT | The official textbook covers core gravitational concepts such as Newton’s law of gravitation, gravitational field, motion of satellites, and energy in a clear and structured manner. |
| NCERT Exemplar Physics (Class 11) | NCERT | Provides higher-order and application-based questions on gravitation for deeper conceptual practice and enhanced problem-solving. |
| Concepts of Physics – Volume 1 | H.C. Verma | Excellent for building conceptual clarity and solving challenging numerical problems related to gravitation and orbital motion. |
| Understanding Physics: Mechanics | D.C. Pandey (Arihant) | Detailed topic-wise explanations, worked examples, and practice questions focused on gravitation, energy, and satellite motion. |
| Physics for Class 11 | R.D. Sharma | Step-by-step theory with a wide variety of solved and unsolved problems on gravitational force, potential energy, and orbital motion. |
| Arihant All-In-One Physics (Class 11) | Arihant | Comprehensive guide with concise theory summaries, formula sheets, solved examples, and practice questions, including past exam problems on gravitation. |
| MTG Chapter-wise Previous Year Questions – Physics | MTG | Helps students practice and analyse past board and competitive exam questions, specifically from the Gravitation chapter. |
NCERT Resources for Gravitation
NCERT resources for the chapter Gravitation are the most reliable and exam-oriented materials for mastering this topic as per the Class 11 Physics syllabus. Some of the main concepts taught in the NCERT textbook and in the exemplar problems are Newton's law of gravitation, gravitational field and potential, acceleration due to gravity, satellite movement, the laws of Kepler, and clearly taught by theory, diagrams and examples. Good conceptual study and numerical solving ability are developed with the help of thorough preparation by NCERT. These materials are crucial to studying in Class 11 board exams and even competitive ones, such as JEE Main and NEET because numerous questions are directly related to the NCERT concepts.
NCERT Subject-Wise Resources
NCERT subject-wise materials are organised and syllabus-based learning content on various subjects, which assists students in developing a good conceptual basis. They consist of textbooks, exemplar problems, and solutions and can thus be very helpful in the preparation for the board exams and even competitive exams such as JEE and NEET.
Practice Questions based on Gravitation
Practice questions from the chapter Gravitation help students strengthen their understanding of gravitational force, motion under gravity, and satellite dynamics. The concepts used in the process of answering these questions include the law of gravitation, variation of acceleration due to gravitation, potential energy and gravitational energy, and orbital motion. Practice will enhance the skills of solving numerical problems, conceptualisation, and precision. The answers to such questions are necessary in passing school exams and competitive exams such as JEE Main and NEET.
Conclusion
The chapter Gravitation gives a solid conceptual base on the universal force of attraction and its influences on objects on the ground and in space. Students can also acquire good analytical and numerical abilities in solving problems by revising major concepts, significant equations and principles like the law of gravity, the acceleration due to gravity, the potential and energy of a gravitational field, and movement of satellites, among others. A systematic and consistent practice approach helps build confidence and accuracy. This preparation is highly effective for performing well in Class 11 examinations as well as competitive exams such as JEE Main and NEET.
Frequently Asked Questions (FAQs)
Newton's Law of Gravitation states that every mass attracts every other mass with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them.
The gravitational force between small objects is extremely weak due to their small masses, so it's negligible compared to Earth's gravitational pull.
Gravity decreases with increasing altitude as the distance from Earth's centre increases. The farther you are from the Earth's surface, the weaker the gravitational pull.
The gravitational constant (G) is approximately 6.674×10−11Nm2/kg2. It is a fundamental constant used in the equation for gravitational force.
Earth has a large mass, and according to Newton's law, all masses attract each other. The Earth's gravitational pull is strong enough to keep everything grounded and gives objects weight.
Gravity is the phenomenon, and gravitational force is the quantity (how much power the gravity of an object has).
The immediate effect would be weightlessness if there were no gravity. While the dispersal of the atmosphere and oceans into space would have happened, as there would be no force to hold them.
The SI unit of gravitational acceleration (g) is m/s².
The moon's gravity pulls the water on Earth's surface, causing the rise and fall of tides.
Escape velocity is the speed an object needs to overcome a planet's gravitational pull and escape into space.
Questions related to
On Question asked by student community
Force applied per unit area is termed as pressure.
Explanation: "Pressure" is defined as the force exerted on a surface divided by the area over which that force is distributed.
Option B is correct .
Other options are incorrect, as acceleration is the rate of change of velocity, gravitation is
Correct Answer: It is the force causing tides due to the stars and the earth
Solution : The correct option is It is the force causing tides due to the stars and the Earth.
The universal law of gravitation primarily describes the gravitational attraction between two masses, such as the