Maxwells Equations - Maxwell’s Four Equations, FAQs

Edited By Team Careers360 | Updated on Nov 12, 2024 10:04 PM IST

In physics, Maxwell's equations/ are a group of coupled fragmentary (partial) differential equations that, in junctions with the Lorentz force law, form the base of classical electromagnetism, classical optics, and electric circuits. Who is Maxwell? Full Name of Maxwell is James Clerk Maxwell, (born June 13, 1831, Edinburgh, Scotland—died November 5, 1879, Cambridge, Cambridge shire, England), Scottish physicist was best known for his research formulation of electromagnetic theory. And this theory is also used as Maxwell’s theory in engineering. In this article we will discuss, what are Maxwell equations? What is Maxwell law? What is the unit of Maxwell equation? What is an example of Maxwell’s equations? What is Maxwell’s equation of electromagnetism? What is the curl of an electric field? Also we have to discuss about derivation of Maxwell’s equation, Maxwell four equations Maxwell electromagnetic theory, Maxwell equation in free space, divergence of electric field, Maxwell equation in differential form Maxwell’s equations in integral form. In this pdf we discuss about class12 and BSc physics Maxwell’s equations. So let’s see,

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

What are Maxwell’s equations?
What are Maxwell’s four equations?
Circulation and curl of electric field:

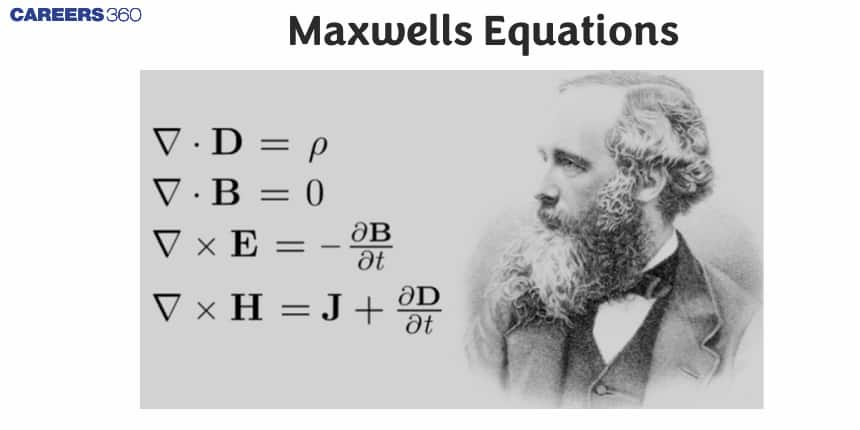
Maxwells Equations - Maxwell’s Four Equations, FAQs

DentalWeakDeer-size_restricted

Also read -

What are Maxwell’s equations?

Maxwell was the primary person to calculate the speed of propagation of electromagnetic waves which was same because the speed of light and came to the conclusion that EM waves and visual light are similar.
These are the set of partial differential equations that form the inspiration of classical electrodynamics, electric circuits and classical optics along side Lorentz force law. These field’s culmination of modern transmission and electrical technologies. Maxwell is represented by “Mx” is the CGS unit of magnetic flux and replaced by the weber, the unit in the SI system.

What is Maxwell’s law?

Gauss law: Gauss law describes the character of the electrical field around electric charges. The law is expressed in terms of electrical charge density and charge density.

∇.D= ρ_V

The inverted triangle is named the divergence operator.

The equations clasp good at any point in space. When the electrical charge make do any somewhere, the divergence of D at that specific point is nonzero, else it's 0.

2. Gauss’ Magnetism Law
the gauss law is one of the examples of Maxwell’s equations; you need to be conversant in Gauss Law for the electrical field to know this equation.

∇.D= ρ_V

∇.B=0

You can see that both the equations represent that the divergence of the field. The highest equation states that the divergence of the electrical flux D equals the quantity of electrical charge density.
The second equation states the divergence of the Magnetic flux (B) is null.

3. Faraday’s Law: The Maxwell–Faraday version of Faraday's law of induction describes how a time varying magnetic flux creates ("induces") an electrical field. In integral form, it states that the work per unit charge required to maneuver a charge around a closed-loop system equals the speed of change of the magnetic flux through the enclosed surface.

Faraday’s Law

∇×E= ∂B/∂t

The electromagnetic induction is that the operating principle behind many electric generators: for instance, a rotating magnet creates a changing magnetic flux, which successively generates an electrical field during a nearby wire.

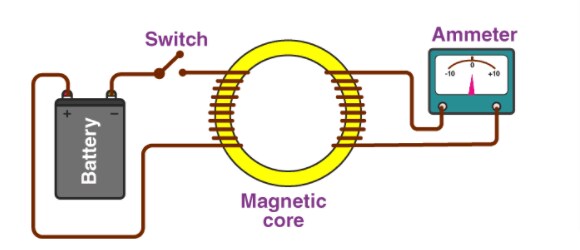
4. Ampere's Law: Ampere’s law with Maxwell's equations shows that magnetic fields are frequently generated in two ways: by current (this was the first "Ampere’s law") and by changing electric fields (this was "Maxwell's addition", which he called displacement current). In integral form, the magnetic flux convinced around any closed-loop system is proportional to the electrical current plus displacement current (proportional to the speed of change of electrical flux) through the enclosed surface.

Maxwell's equations to Ampere’s law are mainly chief: it makes the group of equations mathematically consistent for non-static fields, without changing the laws of Ampere and Gauss for static fields. However, as a consequence, it predicts that a changing magnetic flux induces an electrical field and the other way around. Therefore, these equations permit self-sustaining "electromagnetic waves" to travel via empty space (see electromagnetic radiation equation).

∇×H= ∂D/∂t + J

The speed calculated for electromagnetic waves, which might be forecasted from experiments on charges and currents, matches the speed of light; indeed, light is one sort of electromagnetic wave (as are X-rays, radio waves, and others). Maxwell recognizes the relation between electromagnetic waves and lightweight in 1861, consequently unifying the theories of electromagnetism and optics.

Related Topics Link,

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

What are Maxwell’s four equations?

These equations are named after a Scottish mathematical physicist James Clerk Maxwell, who formulated the classical theory of electromagnetic wave. He produced these questions by including the Lorentz force law betwixt the year 1861 and 1862. Maxwell's first equation presents (proposed) that ‘light is electromagnetic in nature’.

Maxwell’s equations integral form describes how the electric charges and electric currents create magnetic and electric fields. The equation explains how the electric field can create a magnetic field and vice versa.

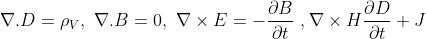
$\nabla.D=\rho_V,\ \nabla. B=0 ,\ \nabla\times E=-\frac{\partial B}{\partial t}\ ,\nabla \times H \frac{\partial D}{\partial t}+J$

Maxwell First Equation
Maxwell first equation is predicated on the Gauss law of electrostatic which states that “when a closed surface integral of electrical flux is usually adequate to charge enclosed over that surface”
Mathematically Gauss law are often expressed as,
Over a closed surface the merchandise of electrical flux vector and surface integral is adequate to the charge enclosed.

a. Maxwell’s equation integral form:

e= q /ϵ₀ ………………..(1)

Also, 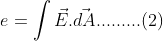$e=\int \vec{E}. \vec{dA}.........(2)$

Contrasting equation (1) and (2)

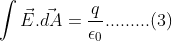
$\int \vec{E}. \vec{dA}=\frac{q}{\epsilon_0}.........(3)$

This is the integral form of 1^st Maxwell’s equations.

b. Maxwell’s Equation in differential form

The value of total charge in terms of volume charge density is

∫q= ρdv

So, the equation (iii) becomes:

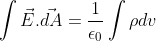
$\int \vec{E}. \vec{dA}=\frac{1}{\epsilon_0}\int \rho dv$

Applying divergence theorem on left-hand side of the above equation, we have:

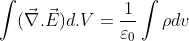
$\int (\vec{\nabla}.\vec{E})d.V= \frac{1}{\varepsilon _0}\int \rho dv$

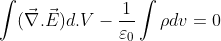
$\int (\vec{\nabla}.\vec{E})d.V-\frac{1}{\varepsilon _0}\int \rho dv=0$

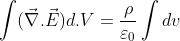
$\int (\vec{\nabla}.\vec{E})d.V= \frac{\rho}{\varepsilon _0}\int dv$

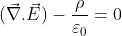
$(\vec{\nabla}.\vec{E})- \frac{\rho}{\varepsilon _0} =0$

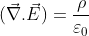
$(\vec{\nabla}.\vec{E})=\frac{\rho}{\varepsilon _0}$

This is the differential form of Maxwell’s 1^st equation

Second Maxwell’s Equations: Gauss’s law for magnetism:

Maxwell second equation is predicated on Gauss law on magneto statics/Magnetism.

Gauss law on magneto statics states that “closed surface integral of magnetic flux is usually adequate to total scalar magnetic flux enclosed within that surface of any shape or size lying in any medium.”

Mathematically it's expressed as – Maxwell’s equation in free space is

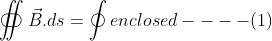
$\oiint_{}^{} \vec{B}.ds=\oint enclosed----(1)$

Hence we can decide that magnetic flux cannot be bounded within a closed surface of any shape.

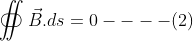
$\oiint_{}^{} \vec{B}.ds= 0----(2)$

Applying Gauss divergence theorem to equation (2) we can turn it (surface integral) into volume integral by picking the divergence of the same vector

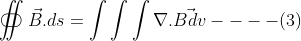
$\oiint_{}^{} \vec{B}.ds= \int \int \int \nabla.\vec{Bdv}----(3)$

Substituting equation (3) in (2) we get-

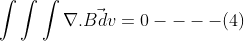
$\int \int \int \nabla.\vec{Bdv}=0----(4)$

Here to understand that the above equation either 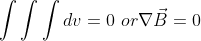$\int \int \int dv=0\ or \nabla \vec{B}=0$ the volume of any body/object can never be 0.

Thus, we arrive at Maxwell’s second equation.

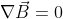
$\nabla \vec{B}=0$

Where,

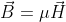$\vec{B}=\mu \vec{H}$ is the flux density

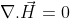$\nabla .\vec{H}=0$ [solonoidal vector is obtained when the divergence of a vector is zero. Irrotational vector is obtained when the vector product is zero]

Third Maxwell’s Equation: Faraday’s Law of Electromagnetic Induction:

How we can find the Maxwell’s Equations derived from Faraday law?

Maxwell modified Faraday's law of induction. It narrates the assembly of electrical fields by a time varying magnetic flux. This law narrated, “Work needed for moving a unit charge around a closed-loop system structure equals the magnetic flux transforming around that specific loop”.

The induced fields lines are almost like that of magnetic flux lines, unless they're superimposed by a static field. This way or technique of electromagnetic induction is that the basic operating principle behind many electric devices like in rotating bar magnets for creating changing magnetic fields, which further produces electric fields during a nearby wire.

The Earth's magnetic flux is altered during a geomagnetic storm, thanks to a surge within the flux of charged particles, which further induces an electrical field in Earth's atmosphere.

∈ = -Nd_m / dt-----(1)

Since emf if related to electric field by the relation

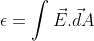
$\epsilon=\int \vec{E}.\vec dA$

Also,

Putting these values in equation (1), we have:

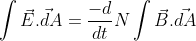
$\int \vec{E}.\vec dA=\frac{-d}{dt}N\int \vec{B}.\vec{dA}$

For N=1, we have

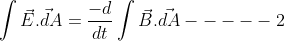
$\int \vec{E}.\vec dA=\frac{-d}{dt}\int \vec{B}.\vec{dA}-----2$

This is the integral formula of Maxwell’s third equation.

Adding stoke’s theorem on L.H.S of equation (2), we have:

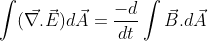
$\int ( \vec{\nabla.}\vec{E})d \vec{A}=\frac{-d}{dt}\int \vec{B}.d \vec{A}$

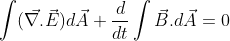
$\int ( \vec{\nabla.}\vec{E})d \vec{A}+\frac{d}{dt}\int \vec{B}.d \vec{A}=0$

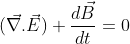
$( \vec{\nabla.}\vec{E})+\frac{d \vec B}{dt}=0$

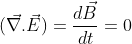
$( \vec{\nabla.}\vec{E})=\frac{d \vec B}{dt}=0$

So, this is the differential form of Maxwell’s third equation.

4. Maxwell’s fourth equations: Ampere's law

According to Ampere’s law with Maxwell addition, “magnetic field can either be created by current or by altering the electrical field. The primary statement is as per Ampere’s law whereas the later is consistent with Maxwell’s addition, the displacement current. The induced magnetic flux around any closed-loop system is directly proportional to the electrical current and therefore the displacement current through that closed surface.

Maxwell's addition to the Ampère's establishes a relationship to form a group of equations mathematically according to the non-static fields, without changing the Ampère's and Gauss's laws for static fields. However, a changing field produces a magnetic flux and the other way around. Therefore, these equations create an opportunity for self-sustaining "electromagnetic waves" to travel through vacuum.

The speed of electromagnetic waves is adequate to the speed of sunshine as per the calculations and observations. Light is additionally a kind of electromagnetic wave (like X-rays and radio waves).

This is a magnetic core memory (1954), and uses Ampère's law. Each core stores data of the size of 1 bit.

Also Read:

Circulation and curl of electric field:

Surface Σ with closed boundary ∂Σ. F might be the E or B fields. Again, n is that the unit normal. (The curl of a vector field doesn't literally appear as if the "circulations", this is often a heuristic depiction.)

By the Kelvin–Stokes theorem we will rewrite the road integrals of the fields round the closed boundary curve ∂Σ to an integral of the "circulation of the fields" (i.e. their curls) over a surface it bounds, i.e.

Hence the modified Ampere law in integral form can be rewritten as

Ampere law in integral

Since Σ are often pick out arbitrarily, e.g. as an arbitrary small, arbitrary oriented, and arbitrary centered disk, we culminate that the integrand is zero if Ampere's modified law in differential equations form is satisfied. The equivalence of Faraday's law in differential and integral form shows as well.

The line integrals and curls are comparable to quantities in classical fluid dynamics: the circulation of a fluid is that the line integral of the fluid's flow velocity field around a closed-loop system, and therefore the velocity of the fluid is that of the curl of the speed field.

A Maxwell rule is a principle of electromagnetism: each part of an electric circuit taking current occurrences such mechanical forces because of its own or to any superposed magnetic field as would purpose the circuit to link with a maximum of magnetic flux.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What's the importance/significance of the Maxwell Equation?

This equation describes or explains how magnetic & electric fields are produced by variations in their current & charges. These equations explains how varying electric and magnetic fields travel at the speed of light .Maxwell's equations are the building blocks of all modern machines or devices such as mobile phones, computers and electricity.

2. What is the application of Maxwell equation?

There are many uses and applications of Maxwell's equations. By understanding electromagnetism, we are ready to create images of the body using MRI scanners in hospitals; we've created mag tape, generated electricity, and built computers. This equation will give us the voltage produced within the coil.

3. One Maxwell is equal to?

The centimeter-gram-second emu of magnetic flux adequate to the flux per square centimeter of normal cross section during a region where the magnetic induction is one gauss : 10−8 weber.

4. Importance of Maxwell's Relations in Thermodynamics.

Maxwell's equations help in changing the thermodynamic variables from one set to a different. For example, suppose you would like to calculate the change in entropy of a system with reference to a given pressure and at a continuing enthalpy. there's no instrument to live entropy of a system. You’ll however measure the temperature, pressure, and volume of a system much easily.

5. According to Maxwell's hypothesis, a changing field gives rise to

According to Maxwell's EM theory, the EM wave’s propagation contains electric and magnetic flux vibration in mutually perpendicular directions. Thus the changing of the electrical field produces magnetic flux.