To Determine Angle Of Minimum Deviation For A Given Prism Via Graph

The experiment to determine the angle of minimum deviation for a prism involves studying how light bends, or deviates when it passes through a prism. When a ray of light enters a prism, it bends towards the base of the prism due to refraction. As the angle of incidence increases, the angle of deviation first decreases, reaches a minimum value, and then increases again. The angle at which this deviation is the smallest is known as the angle of minimum deviation, and it is a key characteristic of the prism. To determine this angle, we measure the angle of deviation for different angles of incidence and plot a graph between these two angles. The point where the deviation is the least on the graph corresponds to the angle of minimum deviation. This experiment is crucial in understanding the behaviour of light in prisms and is fundamental in applications such as spectroscopy.

Aim

To determine the angle of minimum deviation for a given prism by plotting a graph between the angle of incidence and the angle of deviation.

Apparatus

A drawing board, a white sheet of paper, a prism, drawing pins, a pencil, a half-metre scale, office pins, graph paper and a protractor.

Theory

The refractive index in n of the material of the prism is given by
$
n=\frac{\sin \left(\frac{A+D_m}{2}\right)}{\sin \left(\frac{A}{2}\right)}
$

where, $D_m$ angle of minimum deviation and $A$ angle of the prism.

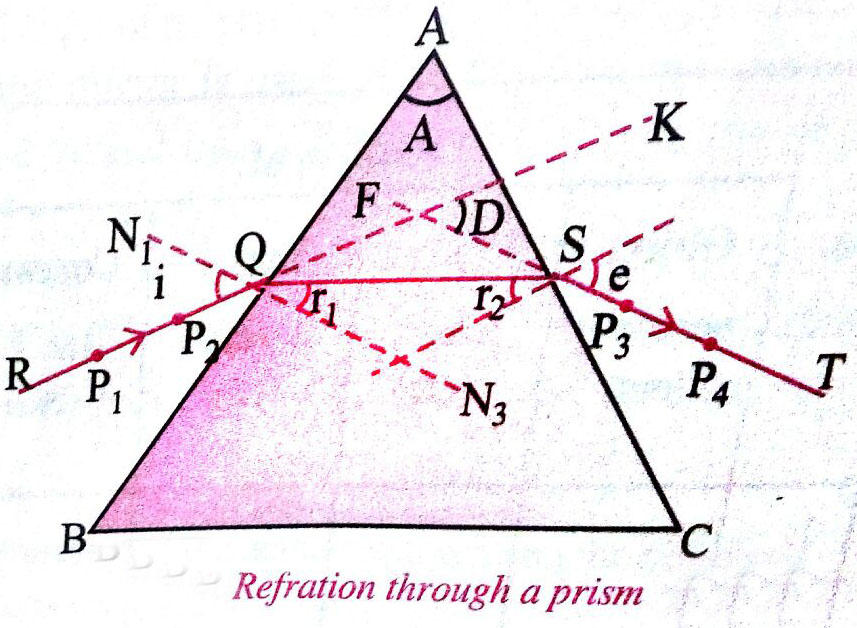
Diagram

Procedure

3. Mark points $Q_1, Q_2, Q_3, \ldots$ on the straight line $X X^{\prime}$ at suitable distances of about 5 cm .
4. Draw normals $\mathrm{N}_1 \mathrm{Q}_1, \mathrm{~N}_2 \mathrm{Q}_2, \mathrm{~N}_3 \mathrm{Q}_3, \cdots$ on points $\mathrm{Q}_1, \mathrm{Q}_2, \mathrm{Q}_3, \ldots$ as shown in the diagram.
5. Draw straight lines $R_1 Q_1, R_2 Q_2, R_3 Q_3, \ldots$ making angles of $35^{\circ}, 40^{\circ}, \ldots 60^{\circ}$ (write the value of the angles on the paper) respectively with the normals.
6. Mark one corner of the prism as $A$ and take it as the edge of the prism for all the observations.
7. Put it prism with its refracting face $A B$ in the line $X X^{\prime}$ and point $Q_1$ in the middle of $A B$.
8. Mark the boundary of the prism.
9. Fix two or more office pin $\mathrm{P}_1$ and $\mathrm{P}_2$ vertically on the line $\mathrm{R}_1 \mathrm{Q}_1 \mathrm{P}_1$ and $\mathrm{P}_2$ vertically on the line $\mathrm{R}_1 \mathrm{Q}_1$ The distance between the pins should be 10 mm or more.
10. Look the images of point $P_1$ and $P_2$ through face $A C$.
11. Close your left eye and bring open your right eye in line with the two images.
12. Fix two office pins $P_3$ and $P_4$ vertically, and 10 cm apart such that the open right eye sees pins $P_4$ and $P_3$ and images of $P_2$ and $P_1$ in one straight line.
13. Remove pins $P_3$ and $P_4$ and encircle their pricks on the paper.
14. Repeat steps 7 to 13 with points $Q_2, Q_3, \ldots$ for $\mathrm{i}=40^{\circ}, \ldots, 60^{\circ}$.

To measure D in different cases

15. Draw straight lines through points $P_3$ and $P_4$ \{ pinpricks) to obtain emergent rays $\mathrm{S}_1 \mathrm{~T}_1, \mathrm{~S}_2 \mathrm{~T}_2, \mathrm{~S}_3 \mathrm{~T}_3, \ldots$
16. Produce $T_1 S_1, T_2 S_2, T_3 S_3, \ldots$ inward in the boundary of the prism to meet produced incident rays $R_1 Q_1$, $\mathrm{R}_2 \mathrm{Q}_2, \mathrm{R}_3 \mathrm{Q}_3, \cdots$ at points $\mathrm{F}_1, \mathrm{~F}_2, \mathrm{~F}_{3, \cdots}$
17. Measure angles $\mathrm{K}_1 \mathrm{~F}_1 \mathrm{~S}_1, \mathrm{~K}_2 \mathrm{~F}_2 \mathrm{~S}_2, \mathrm{~K}_3 \mathrm{~F}_3 S_3, \ldots \ldots$

These give an angle of deviation $\mathrm{D}_1, \mathrm{D}_2, \mathrm{D}_3, \ldots$
18. Write the values of these angles on the paper.

To measure A
19. Measure the angle BAC in the boundary of the prism. This gives angle A.
20. Record your observations.

Calculation

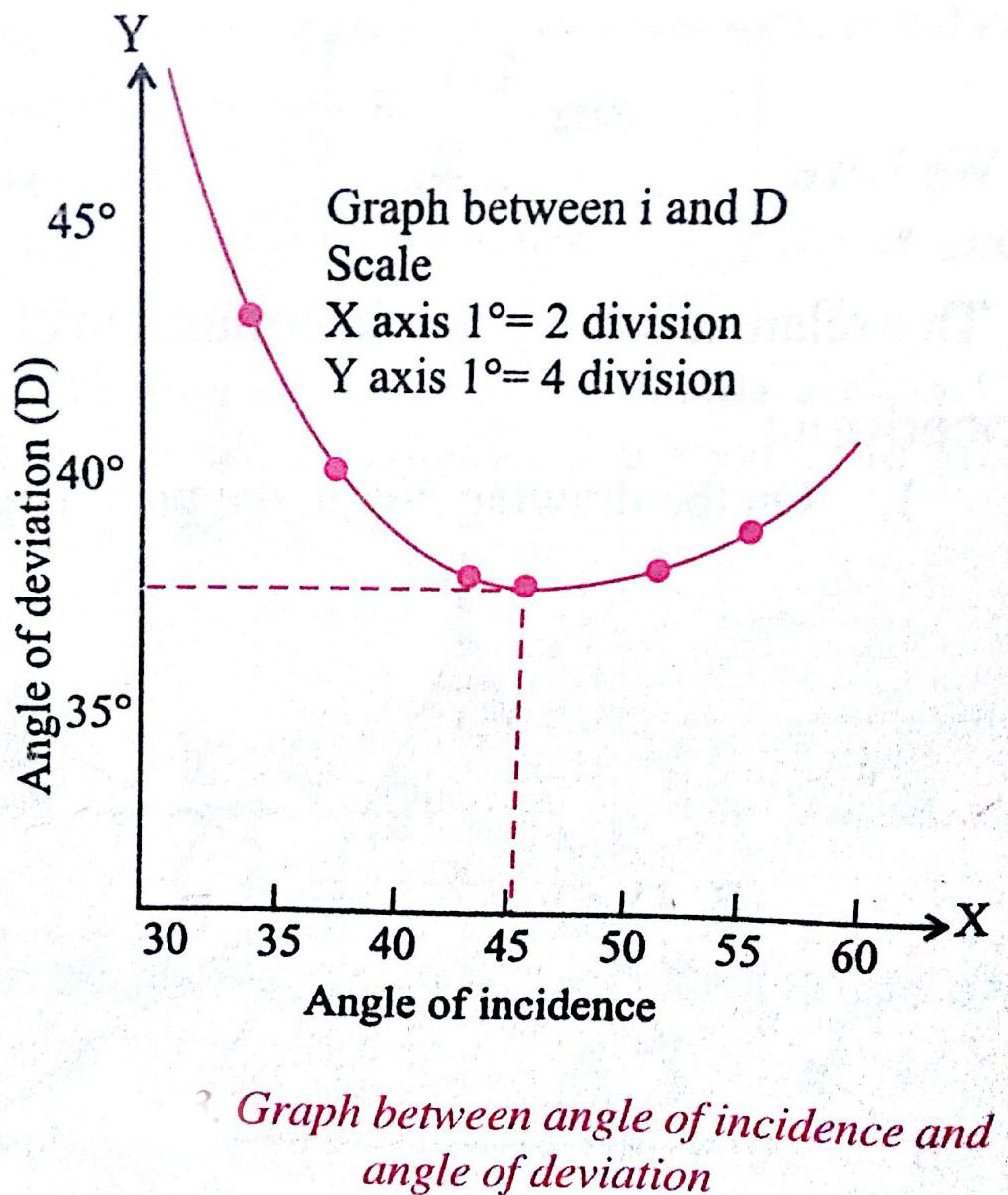
Plot a graph between the angle of incidence $\angle i$ and the angle of deviation $\angle D$ by taking $\angle i$ along X -axis and $\angle D Y$-axis. From this graph, find the value of a single minimum deviation $\mathrm{D}_{\mathrm{m}}$ corresponding to the lowest point of the graph.
Let the value of the angle of minimum deviation, $D_m=\ldots$.

$
\text { Then } n=\frac{\sin \frac{A+D_m}{2}}{\sin A / 2}
$

Result

1. The i-D graph indicates that as the angle of incidence (i) increases, the angle of deviation (D) first decreases, attains a minimum value $\left(D_m\right)$ and then starts increasing for further increase in the angle of incidence.
2. Angle of minimum deviation, $D_m=\ldots \ldots$
3. Refractive index of the material of the prism, $n=\ldots$...

Solved Examples Based on Determining the Angle of Minimum Deviation for a Given Prism by Plotting a Graph Between the Angle of Incidence and the Angle of Deviation

Example 1: On what factors does the angle of deviation depend?

1) The angle of incidence

2) Angle of refraction

3) The material of the prism

4) All of these

Solution

To determine the angle of minimum deviation for a glass prison -

The factors on which the angle of deviation depends are:

1. The angle of Incidence (directly proportional to the angle of deviation)
2. The refractive index of the prism(directly proportional to the angle of deviation)
3. Material of the prism (directly proportional to the angle of deviation)
4. The wavelength of the light passing through (inversely proportional to the angle of deviation)

Example 2: If the angle of the prism is $60$ degrees and the angle of minimum deviation is 37.2 degrees, what will be the refractive index of the prism

1)1.6

2) 1.5

3)1.55

4)1.7

Solution

To calculate min deviation by plotting a graph between the angle of incidence and the angle of deviation

Result

1. Angle of minimum deviation
2. Refractive Index ( $\mu$ )

$
\begin{aligned}
& \mu=\frac{\sin \left(\frac{A+\delta m}{2}\right)}{\sin (A / 2)}=\frac{\sin \left(\frac{97.2}{2}\right)}{\sin 30} \\
& =1.5
\end{aligned}
$

Example 3: An experiment is conducted to determine the refractive index $(n)$ of a glass prism using a spectrometer. A monochromatic light of known wavelength $(\lambda)$ is used. The prism is placed on a table, and the angle of minimum deviation $(D)$ is measured. Calculate the refractive index of the glass prism.

1)5.154
2)3.126
3) 6.255
4) 7.667

Solution

Given values:

Wavelength of light $(\lambda)=589 \mathrm{~nm}$
Angle of minimum deviation $(D)=30^{\circ}$
The refractive index $(n)$ of the glass prism can be calculated using the formula for the angle of minimum deviation:

$
n=\frac{\sin \left(\frac{A+D}{2}\right)}{\sin \left(\frac{D}{2}\right)}
$
Where A is the angle of the prism.
or a prism, $A+D=180^{\circ}$, so $A=180^{\circ}-D$

Substitute the value of A into the formula for $n$
$
n=\frac{\sin \left(\frac{180^{\circ}-D+D}{2}\right)}{\sin \left(\frac{D}{2}\right)}
$
Step 1: Calculate A:

$
A=180^{\circ}-30^{\circ}=150^{\circ}
$
Step 2: Calculate the refractive index $n$ :

$
\begin{aligned}
& n=\frac{\sin \left(\frac{150^{\circ}+30^{\circ}}{2}\right)}{\sin \left(\frac{30^{\circ}}{2}\right)} \\
& n=\frac{\sin \left(\frac{180^{\circ}}{2}\right)}{\sin \left(\frac{15^{\circ}}{2}\right)} \\
& n=\frac{1}{\sin \left(\frac{15^{\circ}}{2}\right)} \\
& n \approx \frac{1}{0.13053} \\
& n \approx 7.667
\end{aligned}
$

The refractive index of the glass prism is approximately 7.667
Hence, the answer is the option (4).

Summary

In this experiment, we determine the angle of minimum deviation for a prism by plotting a graph between the angle of incidence and the angle of deviation. As light passes through the prism, it bends, and the deviation angle changes with the angle of incidence. The graph shows that the deviation decreases to a minimum value before increasing again. The minimum point on this graph gives us the angle of minimum deviation. This experiment helps in understanding how light behaves in a prism and is important for applications like determining the refractive index of materials.