Can any convex lens be used for this experiment?

While theoretically any convex lens can be used, practically it's better to use a lens with a known focal length and good optical quality. The lens should have a focal length that allows for convenient measurement of distances in the experimental setup.

How would using a zoom lens instead of a fixed focal length lens affect the experiment?

Using a zoom lens could allow for more flexibility in adjusting the experimental setup. However, it introduces additional complexity: 1) The focal length must be accurately known for each zoom setting, 2) Zoom lenses may have more aberrations, and 3) There's a risk of accidentally changing the zoom during the experiment, affecting results.

Can this method be adapted for very large convex mirrors, like those used in security or traffic applications?

Yes, this method can be adapted for large convex mirrors, but it presents challenges: 1) Finding a convex lens large enough to capture a significant portion of the reflection, 2) Maintaining alignment over larger distances, 3) Accounting for potential non-uniformities in large mirror surfaces. Scaled-up equipment and careful setup are necessary.

What would happen if the convex mirror was slightly tilted in this experimental setup?

Tilting the convex mirror would change the direction of the reflected light, potentially moving the virtual image off the optical axis. This could lead to: 1) Difficulty in locating the final real image, 2) Introduction of aberrations like astigmatism, 3) Errors in distance measurements. Proper alignment is crucial for accurate results.

What is the impact of atmospheric conditions (like humidity) on the accuracy of this experiment?

Atmospheric conditions can have subtle effects: 1) High humidity can cause condensation on optical surfaces, affecting image quality, 2) Temperature variations can cause thermal expansion, slightly altering distances, 3) Air currents can create shimmer, affecting image stability. Controlled indoor conditions are preferable for accuracy.

How does the convex lens help in finding the focal length of a convex mirror?

The convex lens acts as an imaging device, converting the virtual image formed by the convex mirror into a real image that can be observed on a screen. This allows us to measure distances and apply optical equations to calculate the mirror's focal length.

How does changing the distance between the mirror and lens affect the experiment?

Changing this distance alters the position of the virtual image formed by the mirror relative to the lens. This, in turn, affects the position of the final real image formed by the lens, which is crucial for the calculations.

What role does the focal length of the convex lens play in this experiment?

The focal length of the convex lens is a crucial parameter in the calculations. It determines how the lens will refract light from the mirror's virtual image to form a real image, and it's used in the lens equation to determine the mirror's focal length.

What is the significance of the virtual image formed by the convex mirror in this experiment?

The virtual image formed by the convex mirror acts as the object for the convex lens. Its position relative to the lens determines where the final real image will form, which is crucial for the calculations to find the mirror's focal length.

What are the key measurements needed in this experiment?

The key measurements are: 1) distance between the convex mirror and convex lens, 2) distance between the convex lens and the final real image, and 3) focal length of the convex lens used.

How does the curvature of the convex mirror affect the experiment?

The curvature of the convex mirror determines its focal length. A more curved mirror will have a shorter focal length, resulting in a virtual image closer to the mirror. This affects the position of the final real image formed by the lens.

What would happen if a diverging lens was used instead of a converging lens in this experiment?

A diverging lens would not work for this experiment because it cannot form a real image of the virtual image created by the convex mirror. Diverging lenses only form virtual images, which cannot be projected onto a screen for measurement.

What would happen if the convex mirror was replaced with a plane mirror in this setup?

If a plane mirror was used, the virtual image would form at the same distance behind the mirror as the object is in front. The lens would then form a real image of this virtual image. This setup could be used to verify the focal length of the lens, but not to measure a mirror's focal length.

How does the distance between the light source and the convex mirror affect the experiment?

The distance between the light source and convex mirror doesn't directly affect the focal length measurement. However, it influences the size and brightness of the virtual image. A closer source generally produces a larger, brighter virtual image, which may be easier to work with.

What would happen if the convex mirror and convex lens had the same focal length?

If the convex mirror and convex lens have the same focal length, it doesn't fundamentally change the experiment. However, it might result in the final real image forming at a distance that's convenient for measurement, potentially at twice the focal length of the lens from the lens position.

How does the intensity of light affect the accuracy of this experiment?

The intensity of light doesn't directly affect the focal length measurement. However, brighter light can make it easier to see and locate the final image clearly, potentially improving the accuracy of distance measurements.

How does the distance between the lens and the screen affect the sharpness of the final image?

The sharpness of the final image is best when the screen is placed exactly where the real image forms. Moving the screen closer or farther from this position will result in a blurred image, making it harder to accurately locate the image position.

How does the size of the convex mirror impact the experiment?

The size of the convex mirror doesn't directly affect the focal length measurement. However, a larger mirror may be easier to work with as it provides a larger reflecting surface, potentially improving the clarity of the image and ease of alignment.

Can this method be used to find the focal length of a convex mirror with very large curvature (small focal length)?

Yes, this method can be used for convex mirrors with small focal lengths. However, for very curved mirrors, the virtual image will be very close to the mirror surface, which may require a lens with a short focal length and careful measurement to get accurate results.

How does astigmatism in the convex lens impact the focal length measurement of the mirror?

Astigmatism in the convex lens can lead to distorted or blurred images, making it difficult to accurately locate the image position. This can introduce errors in distance measurements and consequently in the calculated focal length of the mirror. Using a high-quality, aberration-corrected lens is important for accurate results.

What precautions should be taken to ensure the optical axis is properly aligned in this experiment?

To ensure proper alignment: 1) Use an optical bench if available, 2) Ensure the centers of the mirror, lens, and screen are at the same height, 3) Use a laser or straight edge to check alignment, 4) Minimize any tilting of components, and 5) Use adjustable mounts for fine-tuning positions.

How does the aperture size of the convex lens affect the experiment?

The aperture size of the convex lens affects the amount of light gathered and the depth of field. A larger aperture collects more light, potentially creating a brighter image, but may introduce more aberrations. A smaller aperture reduces aberrations but may result in a dimmer image. The optimal aperture balances these factors for clear, measurable images.

Can this method be used to measure the focal length of a convex mirror at different points on its surface?

Yes, this method can be used to measure the focal length at different points on the mirror's surface. By adjusting the incident light to reflect from different areas, you can check if the focal length is consistent across the surface, which is useful for detecting manufacturing defects or non-uniform curvature.

How does the quality of the mirror's reflecting surface affect the experiment?

The quality of the mirror's reflecting surface affects the clarity and intensity of the reflected light. A poor-quality surface can lead to a dim or distorted virtual image, making it harder to locate the final real image accurately. This can introduce errors in the focal length calculation.

What are the potential sources of error in this experiment?

Potential sources of error include: 1) inaccurate measurement of distances, 2) imperfect alignment of the mirror, lens, and screen, 3) aberrations in the lens, 4) parallax errors in reading measurements, and 5) uncertainties in the focal length of the convex lens used.

How does the wavelength of light affect the focal length measurement in this experiment?

The wavelength of light can slightly affect the focal length measurement due to chromatic aberration in the lens. Different wavelengths focus at slightly different points, which can introduce small errors. Using monochromatic light can minimize this effect.

How does the thickness of the convex lens affect the focal length measurement of the mirror?

The thickness of the convex lens doesn't directly affect the mirror's focal length measurement. However, thicker lenses may introduce more aberrations and make it harder to precisely locate the principal planes, potentially affecting the accuracy of measurements.

What happens if the convex lens is placed at its focal length from the convex mirror?

If the convex lens is placed at its focal length from the convex mirror, the final image will form at infinity (very far away). This is because the virtual image from the mirror coincides with the focal point of the lens, resulting in parallel rays after refraction.

How does the magnification of the final image relate to the focal length of the convex mirror?

The magnification of the final image doesn't directly relate to the focal length of the convex mirror. It's more dependent on the relative positions of the mirror, lens, and screen. However, mirrors with shorter focal lengths generally produce smaller virtual images.

Why can't we directly measure the focal length of a convex mirror like we do for concave mirrors?

Convex mirrors always form virtual images behind the mirror, which we can't project onto a screen. This makes direct measurement impossible, so we need to use indirect methods like the convex lens technique to determine the focal length.

What is the relationship between the radius of curvature and the focal length of the convex mirror?

For a spherical convex mirror, the focal length (f) is half the radius of curvature (R). This relationship is expressed as f = R/2. Understanding this helps in interpreting the results of the experiment.

What is the principle behind finding the focal length of a convex mirror using a convex lens?

The principle involves using the convex lens to create a real image of the convex mirror's virtual image. By measuring the distances between the lens, mirror, and image, we can apply the mirror and lens equations to calculate the focal length of the convex mirror.

How does the refractive index of the lens material affect the experiment?

The refractive index of the lens material affects its focal length. As long as the focal length of the lens is accurately known, the refractive index doesn't directly impact the experiment. However, lenses with higher refractive indices may have more pronounced aberrations.

Can this method be used to find the focal length of a concave mirror?

While this specific method is designed for convex mirrors, a similar principle using a convex lens can be applied to concave mirrors. However, the setup and calculations would be different due to the nature of images formed by concave mirrors.

How does the shape of the convex mirror (spherical vs. parabolic) affect the accuracy of this method?

This method assumes a spherical mirror. For parabolic convex mirrors, there might be slight discrepancies as the relationship between focal length and curvature differs. However, for most practical purposes and small mirrors, the difference is negligible, and the method remains valid.

What role does the principle of reversibility of light play in this experiment?

The principle of reversibility of light underpins this experiment. It allows us to treat the virtual image formed by the convex mirror as a real object for the convex lens, even though light doesn't actually originate from that point. This principle ensures that the optical paths and equations remain valid in both directions.

How does the concept of optical power relate to this experiment?

Optical power, measured in diopters, is the reciprocal of focal length in meters. While we typically calculate focal length, understanding optical power can provide intuition about the strength of the mirror's curvature. A mirror with higher optical power (shorter focal length) will create a virtual image closer to its surface.

How does the distance between the convex mirror and convex lens affect the magnification of the final image?

As the distance between the mirror and lens increases, the virtual image from the mirror moves closer to the lens's focal point. This generally results in a larger final real image. The magnification depends on both this distance and the distance from the lens to the screen where the final image forms.

To find focal length of a convex mirror using convex lens

Physics
Experimental skills
To Find Focal Length Of A Convex Mirror Using Convex Lens

To find focal length of a convex mirror using convex lens

Vishal kumarUpdated on 02 Jul 2025, 07:29 PM IST

To determine the focal length of a convex mirror, we can use a convex lens in an experimental setup. A convex mirror always forms a virtual, diminished, and upright image, while a convex lens can form a real image of an object. By placing an object in front of a convex lens, we first obtain a real image on a screen. Then, by positioning the convex mirror behind the convex lens, the mirror reflects the image back through the lens, forming a secondary image. This secondary image appears to come from behind the mirror, and by adjusting the distances until the image on the screen coincides with the original object position, we can apply the lens formula to calculate the focal length of the convex mirror. This experiment combines the properties of lenses and mirrors to find the focal length of the convex mirror, which is typically more challenging to measure directly.

This Story also Contains

Aim
Apparatus
Theory
Experiment Arrangement and Ray Diagram
Procedure
Observations
Calculations
Result
Solved Examples Based on Finding Focal Length of a Convex Mirror Using Convex Lens
Summary

Aim

To find the focal length of a convex mirror, using a convex lens.

Apparatus

An optical bench with four uprights (two fixed uprights in the middle, two outer uprights with lateral movement), a convex lens (20 cm focal length), a convex mirror, a lens holder, a mirror holder, two optical needles, (one thin, one thick) a knitting needle, and a half metre scale.

Theory

Focal length of a convex mirror $f=\frac{R}{2}$
where R= radius of curvature of the mirror.

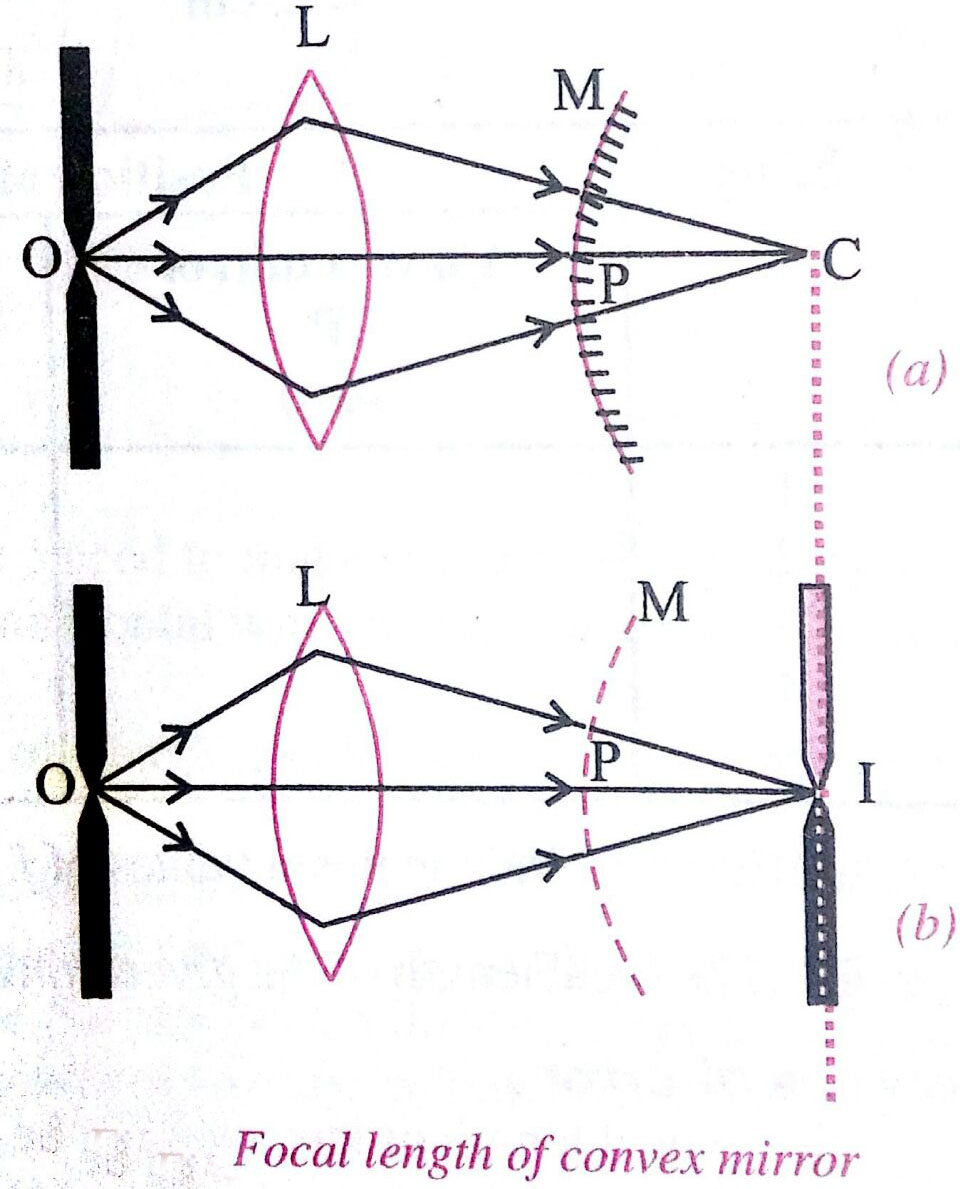
Experiment Arrangement and Ray Diagram

An auxiliary convex lens L is introduced between the convex mirror M and object needle 0 as shown in ray diagram (a). Keeping the object needle at a distance of about 1.5 times the rough focal length of a convex lens, the position of the convex mirror behind the convex lens is so
adjusted that a real and inverted image of object needle O is formed at O itself. Under such conditions, the light rays are incident normally over the convex mirror to retrace their path. In the absence of a convex mirror, these rays would have met at the centre of curvature C of the convex mirror. The distance PC gives the radius of curvature R of the mirror.

To locate the position of C, the convex mirror is removed (without disturbing the object needle O and convex lens L ). An image needle I is put behind the convex lens and moved to a position at which there is no parallax between the tip of the inverted image of the O needle and the tip of the I needle. Position of image needle I gives the position of the centre of curvature C of the mirror M ray diagram (b)

Then PC= PI=R

and $f=\frac{R}{2}=\frac{P I}{2}$

f= focal length

R= radius of curvature of the mirror

Procedure

1. The rough focal length of the convex lens is determined by focusing on a distant object.

To set the lens
2. Clamp the holder with a lens in a fixed upright and keep the upright at the 50 cm mark.
3. Adjust the lens such that its surface is vertical and perpendicular to the length of the optical bench.
4. Keep the upright fixed in this position throughout.

To set the object needle
5 . Take the thin optical needle as an object needle (O). Mount it in outer laterally moveable upright near zero end.
6. Move the object needle upright and clamp it at a distance (in full cm) nearly 1.5 times the obtained
the rough focal length of the lens.

7. Adjust the height of the object needle to make its tip lie on a horizontal line through the optical centre of the lens.
8. Note the position of the index mark on the base of the object needle upright.

To set the convex mirror
9. Clamp the holder with a convex mirror in the second fixed upright near the lens, keeping the reflecting surface of the mirror towards the lens.
10. Adjust the height of the mirror to make its pole lie on a horizontal line through the optical centre of the lens.

11. Make the mirror surface vertical and perpendicular to the length of the optical bench (the principal
axes of mirror and lens must coincide.)
12. Move towards the zero end of the optical bench (where the object needle is mounted).
13. Closing left eye, keep open right eye about 30 cm away from the tip of the object needle.

14. See the inverted image of the object needle (formed by reflection from the convex mirror).
15. Keep the eye in a position at which the tips of the inverted image and the object needle are seen
simultaneously.
16. Adjust the height of the needle so that the two tips are seen in one line with the right open eye.

17. Move the eye towards the right. The tips will get separated. The tips have parallax.
18. Move the convex mirror back and forth till tip to tip parallax is removed.
19. Note the position of the index mark on the base of the convex mirror upright.

To set the image needle
20. Remove the convex mirror, keeping it upright in its position.
21. With the left eye closed, see with the right open eye from the other end of the optical bench. An inverted and enlarged image of the object needle will be seen. The tip of the image must lie in the middle of the lens.

22. Mount the thick optical needle (image needle) in the fourth upright near the other end of the optical
bench.
23. Adjust the height of the image needle so that its tip is seen in line with the tip of the image when seen with the right open eye.
24. Move the eye towards the right. The tips will get separated. The image tip and the image needle tip have parallax.

25. Remove the parallax tip to tip.
26. Note the position of the index mark on the base of the image needle upright.
27. Record the position of the index marks.

To determine index correction
28. Find index correction for the distance between the pole of the convex mirror and the tip of the image needle.

To get more observations
29. Move the object needle upright towards the lens by 2 cm to get more observation and Repeat the experiment.
30. Move the object needle upright away from the lens (from a position of observation 2 ) by 2 cm to get
more observation and Repeat the experiment.
31 Get more and more observations from the experiment and on the basis of observations find out the focal length of the given convex mirror.

Observations

Rough focal length of the convex lens = .....
The actual length of the knitting needle = .....

Observed distance between image needle I and back of the convex mirror y =...

So Index correction =(x-y)=...

Calculations

1. Write down both observed PI and corrected PI
2. Divide corrected PI by 2 to get f
3. Find the mean of values of f recorded

Result

The focal length of the given convex mirror=....cm

Solved Examples Based on Finding Focal Length of a Convex Mirror Using Convex Lens

Example 1: A convex spherical mirror has a focal length of -20 cm. An object is placed 10 cm in front of the mirror on the mirror axis, where is the mirror located.

1) 6.7 cm in front of the mirror

2) 20 cm behind the mirror

3) 6.7 cm behind the mirror

4) 20 cm in front of the mirror

Solution

To find the focal length of a convex mirror using a convex lens

$\begin{aligned} & \mathrm{PC}=\mathrm{PI}-\mathrm{R} \\ & f=\frac{R}{2}=\frac{P I}{2} \\ & \mathrm{f}=-20 \mathrm{~cm}, \mathrm{u}=10 \mathrm{~cm} \\ & \frac{1}{v}=\frac{1}{f}-\frac{1}{u}=-\frac{1}{20}-\frac{1}{10}=\frac{3}{-20} \\ & v=\frac{-20}{3} \mathrm{~cm}=-6.7 \mathrm{~cm}\end{aligned}$

$\therefore$ Image id 6.7 cm behind the mirror

Hence, the answer is the option (3).

Example 2: You are provided with a convex lens and a distant object. Using the parallax method, determine the focal length of the convex lens. The lens is placed in front of the object, and you observe the apparent shift when viewing the object through the lens from different angles.
Given:
• Distance between the object and the lens, Do = 50 cm
• Apparent shift of the object, d = 2 cm
• Distance between your eyes and the lens, De = 25 cm

Assumptions:
• The lens is thin and the lens thickness is negligible.
• The lens is properly aligned and centred.

1) 14.12 cm

2) 17.87 cm

3) 16.67 cm

4) 15.26 cm

Solution

Apply the parallax method formula to calculate the focal length (f) of the convex lens:

$
f=\frac{D_o \times D_e}{D_o+D_e} f=\frac{50 \mathrm{~cm} \times 25 \mathrm{~cm}}{50 \mathrm{~cm}+25 \mathrm{~cm}}
$
Substitute the given values into the formula:

$
\begin{aligned}
& f=\frac{50 \mathrm{~cm} \times 25 \mathrm{~cm}}{50 \mathrm{~cm}+25 \mathrm{~cm}} \\
& f=16.67 \mathrm{~cm}
\end{aligned}
$
The focal length of the convex lens using the parallax method is approximately 16.67 cm.

Hence, the answer is the option (3).

Example 3: You are provided with a convex mirror, a concave mirror, and a convex lens. Using the parallax method, determine the focal lengths of these optical devices. For each case, the object is placed at a certain distance, and you observe the apparent shift when viewing the object through the optical device from different angles.

Given:

• Distance between the object and the optical device, Do = 60 cm
• Apparent shift of the object, d = 3 cm
• Distance between your eyes and the optical device, De = 30 cm

Assumptions:
• The optical devices are properly aligned and centred.
• For convex mirror and lens, the object is virtual.

1) 20 cm, -20 cm , 20 cm

2)-20 cm, -20 cm , 20 cm

3) 20 cm, 20 cm , 20 cm

4)20 cm, -20 cm , -20 cm

Solution

For Convex Mirror:
1. Apply the parallax method formula to calculate the focal length (f) of the convex mirror:

$
f=\frac{D_o \cdot D e}{D_o-D_e}
$

2. Substitute the given values into the formula:

$
f=\frac{60 \mathrm{~cm} \cdot 30 \mathrm{~cm}}{60 \mathrm{~cm}-30 \mathrm{~cm}}
$

3. Calculate the focal length:

$
f=-20 \mathrm{~cm}
$
For Concave Mirror:
1. Apply the same parallax method formula to calculate the focal length ( $f$ ) of the concave mirror:

$
f=\frac{D_o \cdot D e}{D_o-D_e}
$

2. Substitute the given values into the formula:

$
f=\frac{60 \mathrm{~cm} .30 \mathrm{~cm}}{60 \mathrm{~cm}-30 \mathrm{~cm}}
$

3. Calculate the focal length:

f = −20 cm

For Convex Lens:

1. Apply the parallax method formula to calculate the focal length (f) of the convex lens:
$
f=\frac{D_o \cdot D e}{D_o+D_e}
$

2. Substitute the given values into the formula:

$
f=\frac{60 \mathrm{~cm} \cdot 30 \mathrm{~cm}}{60 \mathrm{~cm}+30 \mathrm{~cm}}
$

3. Calculate the focal length:

$
\mathrm{f}=20 \mathrm{~cm}
$

The focal lengths of the optical devices, determined using the parallax method, are as follows:
• For the convex mirror: f = 20 cm
• For the concave mirror: f = -20 cm
• For the convex lens: f = 20 cm
The parallax method involves observing the apparent shift in the position of the object when viewed through the optical device from different angles. By measuring the distances and applying the parallax formula, you can calculate the focal lengths of the devices.
Hence, the answer is the option(1).

Example 4: You are provided with a convex mirror. To determine its focal length using the parallax method, follow these steps:
1. Set up the convex mirror on a stand and place an object at a distance of 60 cm in front of the mirror.
2. Observe the object through the convex mirror while moving your head from side to side, noting the apparent shift in the position of the object.

3. Measure the distance between your eyes and the mirror to be 25 cm.
Given:
• Distance between the object and the convex mirror, Do = 60 cm
• Apparent shift of the object, d = 6 cm
• Distance between your eyes and the convex mirror, De = 25 cm

Assumptions:
• The convex mirror is properly aligned and positioned.

1) -30.2 cm

2) -33.7 cm

3) -37.5 cm

4) -29.1 cm

Solution

Apply the parallax method formula to calculate the focal length (f) of the convex mirror:
$
f=\frac{D_o \cdot D_e}{D_o-D_e}
$
Substitute the given values into the formula:

$
f=\frac{60 \mathrm{~cm} \cdot 25 \mathrm{~cm}}{60 \mathrm{~cm}-25 \mathrm{~cm}}
$

Calculate the focal length:

f = −37.5 cm
The focal length of the convex mirror, determined using the parallax method, is approximately −37.5 cm.

Hence, the answer is the option (3).

Summary

To find the focal length of a convex mirror, we use a convex lens to project a real image onto a screen. By placing the convex mirror behind the lens, the mirror reflects the image back through the lens, forming a secondary image. By adjusting the setup so that the secondary image overlaps with the original object's position, we can calculate the focal length of the convex mirror using the lens formula. This method provides an effective way to measure the focal length of a convex mirror, demonstrating the interplay between lenses and mirrors in optical systems.

Frequently Asked Questions (FAQs)

Q: How does the concept of wavefront curvature relate to the formation of images in this experiment?

Wavefront

Q: How does the concept of conjugate points apply in this experiment?

Conjugate points are pairs of points where an object and its image are located. In this experiment, we have two sets of conjugate points: 1) Between the object and its virtual image in the convex mirror, and 2) Between the virtual image (acting as an object) and the final real image formed by the lens. Understanding these relationships is key to applying the relevant equations.

Q: Can this method be used to measure the focal length of a convex mirror if the focal length of the convex lens is unknown?

While it's possible to set up equations using unknown focal lengths for both the mirror and lens, solving them would be challenging and likely lead to ambiguous results. For practical purposes, it's essential to know the focal length of the convex lens to accurately determine the focal length of the convex mirror.

Q: How does the principle of minimum deviation apply to this experimental setup?

The principle of minimum deviation isn't directly applicable to this setup as it primarily relates to prisms. However, the concept of optimal alignment is relevant. The clearest image and most accurate measurements are obtained when the optical components are perfectly aligned along the optical axis, minimizing any angular deviations.

Q: What would be the effect of using a frosted or diffuse screen instead of a clear one for observing the final image?

Using a frosted or diffuse screen can make it easier to view the final image from different angles, reducing parallax errors. However, it may slightly blur the image edges, making precise location of the image more challenging. The choice depends on the balance between ease of viewing and precision of measurement.

Q: How does the concept of depth of focus affect the accuracy of locating the final image in this experiment?

Depth of focus refers to the range over which the image appears acceptably sharp. A larger depth of focus (which occurs with smaller lens apertures) can make it more difficult to pinpoint the exact location of the sharpest image. This can introduce small errors in measuring the image distance, affecting the calculated focal length.

Q: Can this method be adapted to measure the focal length of a convex mirror using digital imaging techniques instead of a physical screen?

Yes, digital imaging techniques can be adapted for this experiment. A digital camera could replace the screen, allowing for precise measurement of image sharpness and position. This could potentially increase accuracy by using software to analyze image quality and exact focusing distance, minimizing human error in locating the image position.

Q: How does the wavelength dependence of the lens's focal length (chromatic aberration) affect the accuracy of the mirror's focal length measurement?

Chromatic aberration in the lens can lead to slightly different image positions for different colors. This can blur the final image and introduce uncertainty in locating its exact position. Using monochromatic light or an achromatic lens can minimize this effect, improving the accuracy of the mirror's focal length measurement.

Q: What would be the effect of placing a diffraction grating between the mirror and lens in this setup?

Placing a diffraction grating between the mirror and lens would split the reflected light into multiple beams at different angles. This would create multiple images, each corresponding to a different order of diffraction. While interesting for studying diffraction, it would complicate the focal length measurement of the mirror and is not recommended for this specific experiment.

Q: What is the significance of the center of curvature in this experiment, even though we can't directly observe it?

While we can't directly observe the center of curvature, it's conceptually important. The center of curvature is twice the focal length from the mirror surface. Understanding this relationship helps in interpreting the calculated focal length and relating it to the mirror's physical properties.

Articles

Dermatology Courses After 12th - Eligibility Criteria & Top Institutes

Sep 04, 2025

Gujarat Paramedical Merit List 2025 Revised (Out): Download PDF Rank List

Sep 04, 2025

How Online Degree Exams are Conducted in India?

Sep 01, 2025

BiPC Courses After 12th - Fees, Eligibility, Duration & Top Institutes

Aug 25, 2025