Adsorption Isotherms Applications - Explain, FAQs
Have you ever wondered how gases or liquids stick to the surface of solids? What determines the amount of a substance that can be adsorbed at a given temperature and pressure? These questions are answered by adsorption isotherms. It shows the relationship between the amount of substance adsorbed on a solid surface and its pressure (for gases) or concentration (for liquids) at a constant temperature
This Story also Contains
- Adsorption Isotherm
- Adsorption Isotherms: Understanding and Implications
- Types of Adsorption Isotherms
- Relevance and Applications
- Some Solved Examples
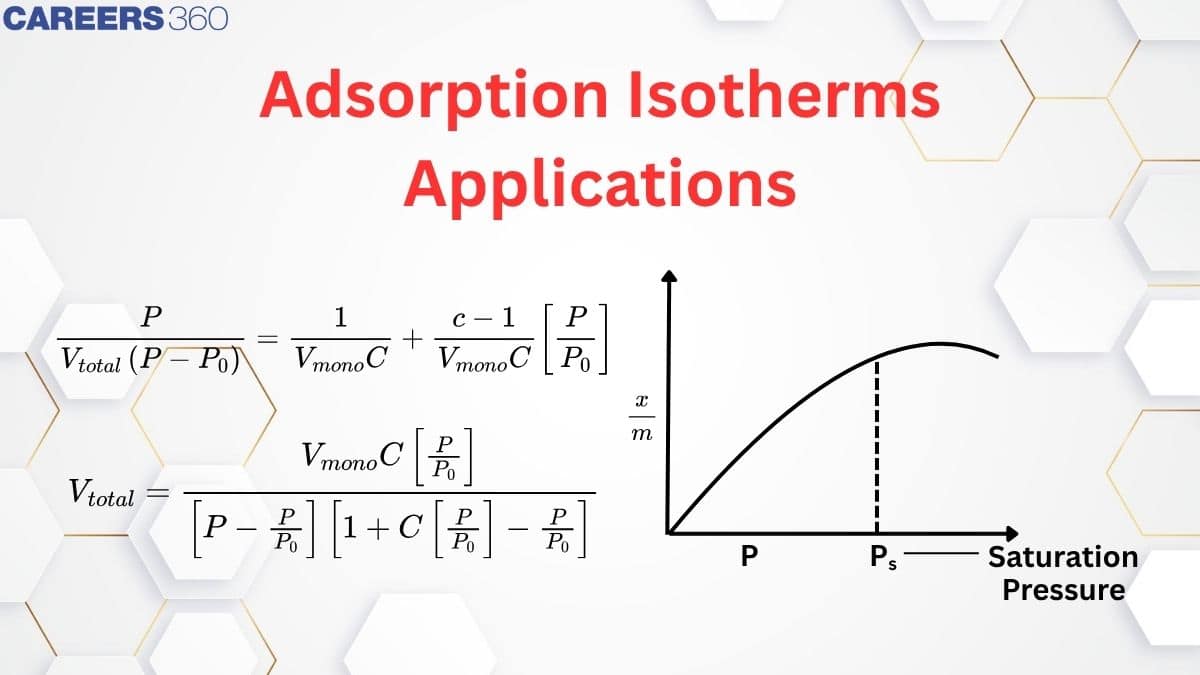
Adsorption Isotherm
The variation in the amount of gas adsorbed by the adsorbent with pressure at constant temperature can be expressed by means of a curve termed as adsorption isotherm. Or in other words, the plots of extent of adsorption(x/m) vs pressure at constant temperature are called Adsorption isotherms.
Here 'x' refers to the mass of gas adsorbed by 'm' the mass of adsorbent.
Factors Affecting Adsorption Isotherm
The extent of adsorption increases with the increase of surface area per unit mass of the adsorbent at a given temperature and pressure.
Also read -
Adsorption Isotherms: Understanding and Implications
Adsorption isotherms are graphic representations of the interaction of adsorbate-adsorbent at constant temperature. It plots the amount of adsorbate on the adsorbent versus its fluid-phase concentration to project a view of the adsorption process. Keywords:
- Adsorbate: It means the adsorbed substance.
- Adsorbent: It refers to the material on which adsorption will take place.
- Isotherm: It is the curve showing the variation of adsorbate concentration under constant temperature with its adsorption extent.
The characteristic studies of adsorption isotherms would make it possible to understand the surface properties and capacities of different adsorbents so an effective adsorption system could be designed.
Types of Adsorption Isotherms
There are different types of adsorption isotherm models, all with their own characteristics. These include:
- Langmuir Isotherm: Assumption of monolayer adsorption onto a surface comprising a finite number of adsorption sites. It is characterized by the equation:
The Langmuir adsorption isotherm equation is given by:
$$\theta=\frac{b P}{1+b P}$$
where:
$\theta$ is the fraction of the surface covered by the adsorbate
P is the pressure of the adsorbate.
? is the Langmuir constant
- Freundlich Isotherm: Applied for heterogeneous surfaces, it can commonly be expressed as:
The Freundlich adsorption isotherm equation is given by:
$$
x / m=k P^{1 / n}
$$
where:
$x / m$ is the amount of adsorbate per unit mass of adsorbent.
$P$ is the pressure of the adsorbate.
$k$ and $n$ are empirical constants specific to the system.
3. BET Isotherm: Generalization of the Langmuir model for multilayer adsorption usually applied for porous materials.
Each model offers insights into different dimensions of the interaction of adsorbate with the surface, hence providing clues to choosing relevant models depending on the application.
Relevance and Applications
Adsorption isotherms find application in the following industrial and research sectors:
- Environmental Engineering: Adsorption isotherms turn out to be useful during water and air treatments in the selection and design of adsorbents for removing contaminants.
- Pharmaceuticals: The principles of adsorption are utilized in drug delivery systems by controlling the release of active ingredients.
- Chemical Engineering: Understanding adsorption isotherms helps in the design of catalysts and reactors.
- Agriculture: In soil science, adsorption isotherms are applied to the study of nutrient uptake and pesticide behavior.
The applicability of adsorption isotherms in academic research falls under very significant application. Characterization of novel materials and understanding their surface properties are fundamentally important in the materials field. They provide insights into the adsorption mechanisms critical in developing innovative solutions in the domain of science.
Also Read:
- NCERT solutions for Class 12 Chemistry Chapter 5 Surface Chemistry
- NCERT Exemplar Class 12 Chemistry Solutions Chapter 5 Surface Chemistry
- NCERT notes Class 12 Chemistry Chapter 5 Surface Chemistry
Recommended topic video on(adsorption isotherms)
Some Solved Examples
Question 1: The curve showing the variation of adsorption with pressure at constant temperature is called?
1) An innovative
2) Adsorption isotherm
3) Adsorption isobar
4) All are incorrect
Solution:
The correct answer is option (2), Adsorption isotherm. An adsorption isotherm represents the relationship between the amount of gas adsorbed by an adsorbent and the pressure of the gas at a constant temperature.
Question 2:
At the equilibrium position in the process of adsorption $\qquad$
1) $\Delta H>0$
2) (correct) $\Delta H=T \Delta S$
3) $\Delta H>T \Delta S$
4) $\Delta H<T \Delta S$
Solution: The answer is option (2).At equilibrium position during adsorption, $\Delta G=\Delta H-T \Delta S=0$ So that $\Delta H=T \Delta S$
Hence, the answer is option (2).
Question 3: For Freundlich adsorption isotherm, a plot of $\log \left(\frac{x}{m}\right)$ (y-axis) and $\log p$ ( $x$-axis) gives a straight line. The intercept and slope for the line are 0.4771 and 2 , respectively. The mass of gas, adsorbed per gram of adsorbent if the initial pressure is 0.04 atm , is $\times 10^{-4} g \cdot(\log 3=0.4771)$
Solution:
So, The mass of gas, adsorbed per gram of adsorbent means Need to find $\mathrm{x} / \mathrm{m}$ which is -
$
\begin{aligned}
& \frac{x}{m}=K P^{1 / n} \\
& \log \left(\frac{x}{m}\right)=\frac{1}{n} \log P+\log K \\
& \text { Slope }=\frac{1}{n}=2 \\
& \text { intercept }=\log K=0.4771 \\
& K=3
\end{aligned}
$
mass of gas adsorbed per gm of adsorbent $=\frac{x}{m}$
$
\frac{\mathrm{x}}{\mathrm{~m}}=3 \times(0.04)^2=48 \times 10^{-4}
$
Hence, the answer is (48)
Practice More Questions With The Link Given Below:
Summary
Adsorption isotherms are among the preferred methods of understanding substance–surface interactions. They guide practical applications in such wide fields as environmental engineering, pharmaceuticals, and even chemical engineering. Knowing the basics of adsorption isotherms, their types, and applications will help us achieve an all-rounded understanding of this key process. The adsorption isotherms can not only help design a viable adsorption system but also enhance our capabilities towards pollution control, advanced material development, and many more.
Also Read
| NCERT Exemplar Class 11th Chemistry Solutions | |
| NCERT Exemplar Class 12th Chemistry Solutions | NCERT Notes Class 12th Chemistry |
| NCERT Exemplar Solutions for All Subjects |
Frequently Asked Questions (FAQs)
Isotherm is a change in a system where the temperature remains constant and it is known as an isothermal process. Here, ΔT = 0. Isotherm, is line drawn on a map or chart joining points with the same temperature. Isotherms are commonly used on a chart indicating constant level.
The release of an adsorbed substance from a surface is referred to as desorption. This is the reversal of the sorption process. Desorption happens when the bulk phase and the adsorbing surface are in a condition of sorption equilibrium. As a result, lowering the bulk phase concentration causes some of the desorbed substance to revert to the bulk state. Desorption process helps the mobility of the mobile phase in chromatography.
The process is unique in that it will only occur if a chemical bond is formed between the adsorbent and the adsorbate. In nature, the process is irreversible. It's an exothermic reaction, which means the temperature rises as a result of the reaction. In chemical adsorption the rate of adsorption is slow when the temperature is low, but as the pressure rises, it happens faster. Chemisorption, like physisorption, is directly proportional to surface area and so increases as surface area grows. The enthalpy is high because the process requires chemical bond formation. It necessitates a specific amount of activation energy.
Adsorption isotherm; Adsorption isotherms have played a critical role in studies of environmental protection and adsorption strategies. The Freundlich and Langmuir isotherms are the two most used approaches for predicting a material's adsorption capacity. At a constant temperature, the Freundlich adsorption isotherm graph is a graph that depicts the fluctuation in the amount of adsorbate(x) adsorbed on the surface of the adsorbent as a function of pressure. The direction of equilibrium in a reaction varies in the direction that stress is relieved, as we know from Le Chatelier's principle. As a result, we can see that when the system is subjected to excessive pressure, the equilibrium moves in the direction of fewer molecules, lowering the pressure in the system.
Removal of colour: To obtain a clear liquid solution, the juice collected from cane is treated with animal charcoal to remove the colouring ingredient.
As Catalysts: Appropriate materials are used as catalysts so that reactants attach to their surface, allowing the reaction to occur more quickly and increasing the rate of reaction.
Isotherm is a change in a system where the temperature remains constant and it is known as an isothermal process. Here, ΔT = 0. Isotherm, is line drawn on a map or chart joining points with the same temperature. Isotherms are commonly used on a chart indicating constant level.
The release of an adsorbed substance from a surface is referred to as desorption. This is the reversal of the sorption process. Desorption happens when the bulk phase and the adsorbing surface are in a condition of sorption equilibrium. As a result, lowering the bulk phase concentration causes some of the desorbed substance to revert to the bulk state. Desorption process helps the mobility of the mobile phase in chromatography.
The process is unique in that it will only occur if a chemical bond is formed between the adsorbent and the adsorbate. In nature, the process is irreversible. It's an exothermic reaction, which means the temperature rises as a result of the reaction. In chemical adsorption the rate of adsorption is slow when the temperature is low, but as the pressure rises, it happens faster. Chemisorption, like physisorption, is directly proportional to surface area and so increases as surface area grows. The enthalpy is high because the process requires chemical bond formation. It necessitates a specific amount of activation energy.
Adsorption isotherm; Adsorption isotherms have played a critical role in studies of environmental protection and adsorption strategies. The Freundlich and Langmuir isotherms are the two most used approaches for predicting a material's adsorption capacity. At a constant temperature, the Freundlich adsorption isotherm graph is a graph that depicts the fluctuation in the amount of adsorbate(x) adsorbed on the surface of the adsorbent as a function of pressure. The direction of equilibrium in a reaction varies in the direction that stress is relieved, as we know from Le Chatelier's principle. As a result, we can see that when the system is subjected to excessive pressure, the equilibrium moves in the direction of fewer molecules, lowering the pressure in the system.
Removal of colour: To obtain a clear liquid solution, the juice collected from cane is treated with animal charcoal to remove the colouring ingredient.
As Catalysts: Appropriate materials are used as catalysts so that reactants attach to their surface, allowing the reaction to occur more quickly and increasing the rate of reaction.
