Ideal Solution

Edited By Team Careers360 | Updated on Oct 10, 2024 11:43 AM IST

The idea of an ideal solution was discovered at the end of 1900 and at the start of 2000 centuries With this discovery various scientists took part in the, main idea by the study of an ideal solution is the study of solutions and the properties of the solution by which the study begins. In 1887, there was a Dutch chemist named Johannes Diderik van der Waals did important studies to understand the behaviour of liquids and gaseous which laid the framework of the concept of the ideal solution.

JEE Main 2025: Chemistry Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Ideal Solution
Some Solved Example
Summary

Ideal Solution - Meaning, Definition, Examples, FAQs

The further advancements in the work come with the work of Gilbert N. Lewis and another British chemist Richard S. Lind. In 1923 paper on the theory of solutions, developed the concept of chemical potential and proposed that an ideal solution follows a behaviour where the enthalpy of mixing is zero. Lind's work, alongside Lewis's, expanded the theoretical framework to explain the deviations observed in real solutions from the ideal solution.

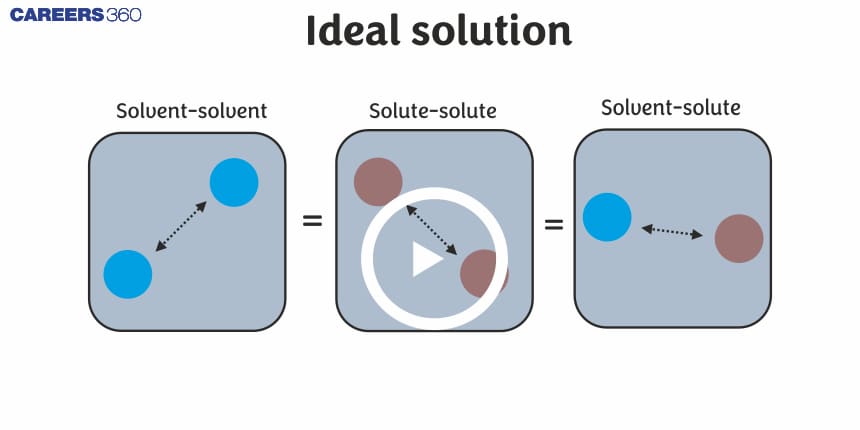
The solutions which obey Raoult’s law for the entire range of composition are called Ideal solutions.

In these solutions, the solute-solute and solvent-solvent interactions are almost similar to solute-solvent interactions (A-B = A-A or B-B interactions). Since the existing forces and the newly formed forces are almost identical, there is no enthalpy change in the mixing of these solutions i.e $\Delta H_{\operatorname{mix}}=0$.

There is no change in the volume during the mixing process i.e.$\Delta V_{\operatorname{mix}}=0$ For example if 1 litre solutions each of liquid A and B are mixed to form an ideal solution, then the solution obtained has a volume equal to 2 litres.

The entropy of mixing is positive as new interactions are introduced into the solution which increases the randomness of the system and hence $\Delta S_{\operatorname{mix}}>0$ The mixing process is spontaneous and hence $\Delta G_{\operatorname{mix}}<0$

These solutions have vapor pressure as predicted by Raoult’s law.
$\begin{aligned} & P_A=P_A^o X_A \\ & P_B=P_B^o X_B \\ & P_T=P_A+P_B\end{aligned}$

Examples of ideal solutions

For the solutions to follow the ideal solution at all ranges of concentrations and temperatures then the molecular size of the liquids should be nearly the same.
For example:

CH₃OH + C₂H₅OH: Both these liquids are polar and have nearly the same size. Thus, this solution is an ideal solution.
C₂H₅Br₂ + C₂H₅Cl₂: Both these liquids are polar and have nearly the same size. Thus, this solution is an ideal solution.
C₂H₅Cl + C₂H₅Br: Both these liquids are polar and have nearly the same size. Thus, this solution is an ideal solution.
C₆H₆ + C₆H₅CH₃: Both these liquids are non-polar and have nearly the same size. Thus, this solution is an ideal solution.
C₂H₅Cl + C₂H₅I: Both these liquids are polar but the size difference between the molecules is large. Thus, this solution is not an ideal solution.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

NCERT Chemistry Notes:

Some Solved Example

Example.1 Equimolal solutions in the same solvent have

1)same boiling point but different freezing point

2)same freezing point but different boiling point

3) (correct)same boiling and same freezing points

4)different boiling and different freezing point

Solution

Raoult's Law -The total vapour pressure of the binary mixture of miscible liquids ideally is given by

$P_T=P_A^0 x_A+P_B^0 x_B$

Where $x_A$ and $x_B$ are mole fractions of A and B in the liquid phase

$P_{A \text { and }}^0 P_B^0$ are vapour pressures of pure liquids.

According to Raoult's law, equimolar solutions of all substances in the same solvent will show the equal value of colligative properties such as elevation in Boiling Point, depression in freezing point, osmotic pressure and relative lowering of vapour pressure.

Hence, the answer is the option (3).

Example.2 A mixture of 100 m mol of $\mathrm{Ca}(\mathrm{OH})_2$ and 2 g of sodium sulphate was dissolved in water and the volume was made up to 100 mL . The mass of calcium sulphate formed and the concentration of $OH^{-}$ in the resulting solution, respectively , are : (Molar mass of $\mathrm{Ca}(\mathrm{OH})_2, \mathrm{Na}_2 \mathrm{SO}_4$ and $\mathrm{CaSO}_4$ , are 74, 143 and 136 g $\mathrm{mol}^{-1}$ , respectively ; $K_{\text {sp }}$ of $\mathrm{Ca}(\mathrm{OH})_2$ is $5.5 \times 10^{-6}$,)

1) (correct)$1.9 \mathrm{~g}, 0.28 \mathrm{~mol} \mathrm{~L}^{-1}$

2)$13.6 \mathrm{~g}, \quad 0.28 \mathrm{molL}^{-1}$

3)$1.9 \mathrm{~g}, 0.14 \mathrm{molL}^{-1}$

4)$13.6 \mathrm{~g}, \quad 0.14 \mathrm{molL}^{-1}$

Solution

Given,

Mol of Na₂SO₄ = 2/142 = 14 m mol

$
\begin{aligned}
& \mathrm{Ca}(\mathrm{OH})_2+\mathrm{Na}_2 \mathrm{SO}_4 \longrightarrow \mathrm{CaSO}_4+2 \mathrm{NaOH} \\
& \begin{array}{llll}
\mathrm{mmol} & 100 \quad 14 & 14 \mathrm{~m} / \mathrm{mol} \quad 28 \mathrm{~m} / \mathrm{mol}
\end{array} \\
&
\end{aligned}
$

Mass of $\mathrm{CaSO}_4=\frac{14 \times 136}{1000}=1.9 \mathrm{gm}$
Molarity of $\mathrm{OH}^{-}=\frac{28}{100}=0.28 \mathrm{~mol} / \mathrm{L}$

Example.3 All of the following form ideal solutions except:

1)$\mathrm{C}_2 \mathrm{H}_5 \mathrm{Br}$ and $\mathrm{C}_2 \mathrm{H}_5 \mathrm{I}$

2)$\mathrm{C}_6 \mathrm{H}_5 \mathrm{Cl}$ and $\mathrm{C}_6 \mathrm{H}_5 \mathrm{Br}$

3)$\mathrm{C}_6 \mathrm{H}_6$ and $\mathrm{C}_6 \mathrm{H}_5 \mathrm{CH}_3$

4) (correct)$\mathrm{C}_2 \mathrm{H}_5 \mathrm{I}$ and $\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$

Solution

$\mathrm{C}_2 \mathrm{H}_5 \mathrm{I}$ and $\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$ do not form an ideal solution.

Hence, the answer is the option (4).

Example.4 Which of the following is incorrect?

1)Relative lowering of vapour pressure is independent of the nature of the solute

2)The vapour pressure is not a colligative property.

3) The vapour pressure of a solution is lower than the vapour pressure of the solvent

4) (correct)The relative lowering of vapour pressure is directly proportional to the original pressure

Solution

The vapour pressure is not a colligative property but lowering of Vapor Pressure is a colligative property of solutions.

According to Raoult's law, the relative lowering in vapour pressure of a dilute solution is equal to the mole fraction of the solute present in the
solution.

Hence, the answer is the option (4).

Example.5 100 mL of liquid A and 25 mL of liquid B are mixed to form a solution of volume 125 mL. Then the solution is:

1) (correct)Ideal

2) Non-ideal with positive deviation

3) Non-ideal with negative deviation

4)Cannot be predicted

Solution

Here,
V_A = 25 mL , V_B = 100 mL
After mixing
V_A + V_B = 125 mL
then,
$\Delta V_{\operatorname{mix}}=125-(100+25)=0$
hence the solution is ideal.
Hence, the answer is the option (1).

Example.6 Liquid and liquid $' N^{\prime}$ form an ideal solution. The vapour pressures of pure liquids $' M^{\prime}$ and $' N^{\prime}$ are $450$ and 700 mmHg, respectively, at the same temperature. Then correct statement is :

$x_M=$ Mole fraction of ${ }^{\prime} M^{\prime}$ in solution;

$x_N=$ Mole fraction of ${ }^{\prime} N^{\prime}$ in solution;

$y_M=$ Mole fraction of $' M$ ' in vapour phase;

$y_N=$ Mole fraction of ${ }^{\prime} N^{\prime}$ in vapour phase)

1) $\frac{x_M}{x_N}=\frac{y_M}{y_N}$

2)$\left(x_M-y_M\right)<\left(x_N-y_N\right)$

3) $\frac{x_M}{x_N}<\frac{y_M}{y_N}$

4) (correct) $\frac{x_M}{x_N}>\frac{y_M}{y_N}$

Solution

The vapour pressures of pure liq. M & N are 450 mm of Hg and 700 mm of Hg respectively,

$\begin{aligned} & P_N^0>P_M^0 \\ & y_N>x_N\end{aligned}$ $(N \rightarrow$ more volatile)

$\begin{aligned} & y_M<x_M \Rightarrow x_M>y_M \\ & y_N<x_N \rightarrow x_N>y_N \\ & \frac{x_M}{x_N}>\frac{y_M}{y_N}\end{aligned}$

Hence, the answer is the option (4).

Summary

An ideal solution is a theoretical concept in chemistry where the components mix perfectly without any change in their properties, such as volume or enthalpy. In an ideal solution, the interaction are the same in both the components either in the other molecules or in the component of the same molecules. there are a lot of benefits of an ideal solution in the field of scientific research and in the various practical application and most of the advantages are as follows the ideal solution is used in predicting the behaviour of mixtures of solutions by predicting their intermolecular forces by which they are joined. And this can be predicted by applying the Raoult's law to determine the vapour pressure.

Also check-

Frequently Asked Questions (FAQs)

1. What are your thoughts on an ideal solution?

A solution where the interaction of component molecules does not vary from the interactions of each component’s molecules. In theory, all solutions obey Raoul’s law, no matter what concentration or temperature they are at.

2. A perfect solution has what characteristics?

There are several characteristics of an ideal solution: (i) mixing volume change should be zero. A mixing heat change of zero is required in (ii).

3. How does Raoul’s Law work?

Roult’s law is a chemical law that indicates how much vapor pressure a solution has based on the mole fraction of the solution. Raoul’s Law is expressed by the formula, Resolution = Χ _solvent x P _solvent

4. Raoul’s law states what?

According to Raoul’s law, a solution's vapor pressure equals the sum of each volatile component's vapor pressure if the mole fraction of that component in the solution is strictly multiplied by that component's vapor pressure.

5. A perfect gas is what?

It is defined as an ideal gas if there are no attractive forces between molecules and all collisions between atoms or molecules occur smoothly. It is probably an image of a series of colliding perfectly hard spheres that cannot communicate.