Conic Sections: Circle, Parabola, Ellipse, Hyperbola - Formulas & Equations

Have you ever wondered how planets orbit in predictable paths around the sun? How does the water from the fountain follow a curved path to reach the ground? What are the shapes associated with these paths and how are they formed? The answer to all these questions lies in the concept of conic sections.

In mathematics, the two-dimensional curves that can be generated as cross-sections when a double cone is cut by a plane at different angles are called conic sections. The curves circle, parabola, hyperbola and ellipse are called conics. These conics have many real-life applications in various fields like Medicine, Architecture, Astronomy, Physics, Design, etc.

This article is about the concept of Class 11 Conic Sections. Now, let's look at the basic concepts in conic sections what is conic section, general equation of conic sections, terms in conic sections, 4 types of conics and definitions, conic section formulas, and examples of conic sections in real life.

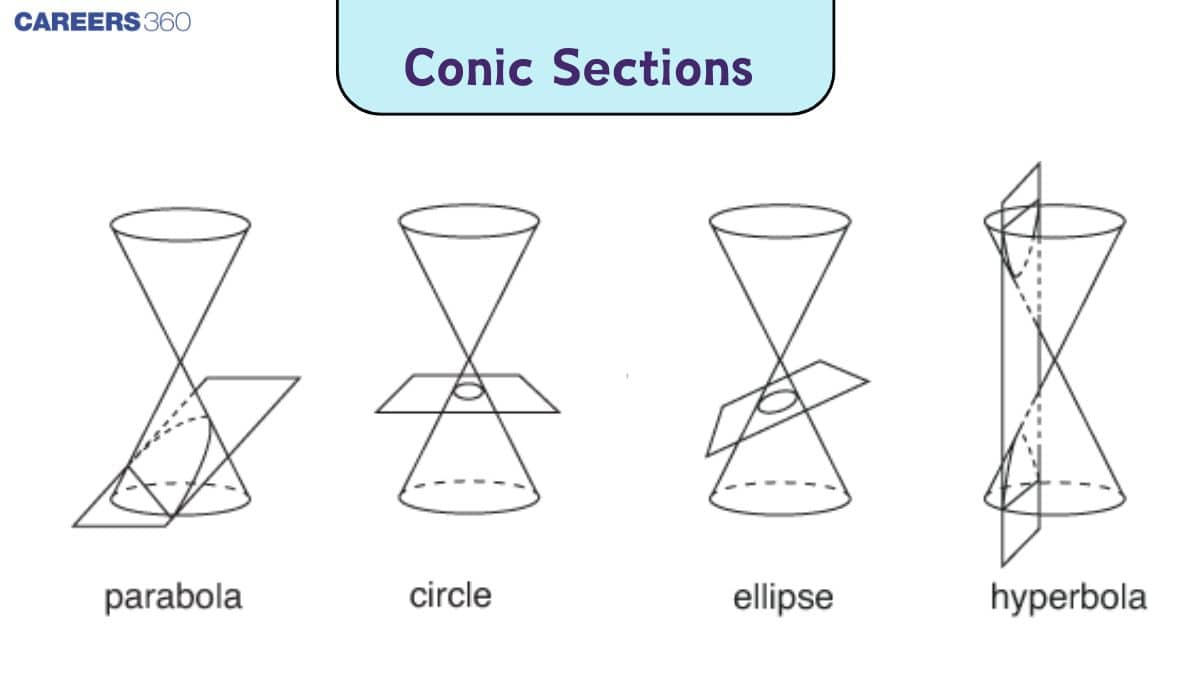
Conic Sections

Conic Sections are the curves obtained by the intersection of circular cones by a plane. The intersection of the plane with the cone can take place either at the vertex of the cone or at any other part of the plane either below or above the vertex. There are 4 conic sections depending on where and how the plane intersects the cone. The conic sections include

• Circle
• Parabola
• Hyperbola
• Ellipse

The general equation of a conic section is $A x^2+B x y+C y^2+D x+E y+F=0$ , where $A, B, C, D, E$, and $F$ are real numbers and $A, B$, and $C$ are nonzero. The values of $A, B, C, D, E$, and $F$ are used to determine the type of the conic section.

Conic Section Parameters

A conic section is the locus of a point that moves in a plane so that its distance from a fixed point is in a constant ratio to its perpendicular distance from a fixed line.

Focus: The fixed point in the conic that defines the curve is called the focus. The parabola has one focus while the ellipse and hyperbola has two each. The circle as derived from an ellipse has both the focus at the same place(centre) and every point of the circle is equidistant from the centre.

Directrix: The fixed line in the conic is called the directrix. It is used to determine the shape of the curve in a constant ratio. A circle does not have any directrix. The parabola has one directrix while the ellipse and the hyperbola have two each.

Eccentricity: The constant ratio between the focus and the directrix is called the eccentricity. It is denoted by 'e'. The value of eccentricity determines how stretched or shaped the curve is.

• $e=1$ then the conic is a circle
• $e=1$ then the conic is a parabola
• $e<1$ then the conic is an ellipse
• $e>1$ then the conic is a hyperbola

Terms in Conic Section

• Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.
• Vertex: The point of intersection of the conic section and the axis is called the vertex of the conic section.
• Double ordinate: Any chord, that is perpendicular to the axis of the conic section, is called a double ordinate of the conic section.
• Focal chord: Any chord passing through the focus is called the focal chord of the conic section.
• Focal distance: The distance between the focus and any point on the conic is known as the focal distance of that point.
• Latus rectum: Any chord passing through the focus and perpendicular to the axis is known as the latus rectum of the conic section.
• Center: The point which bisects every chord of the conic passing through it, is called the center of the conic section.
• Tangent: Tangent to a curve is a line touching the curve only at one point without passing through it.
• Normal: Normal at a point of a curve is the line perpendicular to the tangent and passing through the point of contact.

Circle

A circle is the locus of a moving point such that its distance from a fixed point is constant.

The fixed point is called the centre $( O )$ of the circle and the constant distance is called its radius $(r)$.

Equation of circle

The equation of a circle with centre at $C(h, k)$ and radius $r$ is $(x-h)^2+(y-k)^2=r^2$

Let $\mathrm{P}(\mathrm{x}, \mathrm{y})$ be any point on the circle. Then, by definition, $|C P|=r$.
Using the distance formula, we have
$
\sqrt{(x-h)^2+(y-k)^2}=r
$
i.e.
$
(\mathrm{x}-\mathrm{h})^2+(\mathrm{y}-\mathrm{k})^2=\mathrm{r}^2
$

If the centre of the circle is the origin or $(0,0)$ then the equation of the circle becomes
$
\begin{aligned}
& (x-0)^2+(y-0)^2=r^2 \\
& \text { i.e. } x^2+y^2=r^2
\end{aligned}
$

General Form of Equation of Circle

The equation of a circle with centre at $(\mathrm{h}, \mathrm{k})$ and radius r is
$
\begin{aligned}
& \Rightarrow(x-h)^2+(y-k)^2=r^2 \\
& \Rightarrow x^2+y^2-2 h x-2 k y+h^2+k^2-r^2=0
\end{aligned}
$

Which is of the form :
$
x^2+y^2+2 g x+2 f y+c=0
$

This is known as the general equation of the circle.
To get the radius and centre if only the equation of the circle (ii) is given:
Compare eq (i) and eq (ii)
$
\mathrm{h}=-\mathrm{g}, \mathrm{k}=-\mathrm{h} \text { and } \mathrm{c}=\mathrm{h}^2+\mathrm{k}^2-\mathrm{r}^2
$

Coordinates of the centre $(-\mathrm{g},-\mathrm{f})$
$
\text { Radius }=\sqrt{g^2+f^2-c}
$

Nature of the Circle

For the standard equation of a circle $\mathrm{x}^2+\mathrm{y}^2+2 \mathrm{~g} x+2 \mathrm{fy}+\mathrm{c}=0$ whose radius is given as $\sqrt{g^2+f^2-c}$
Now the following cases arise
1. If $\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}>0$, then the radius of the circle will be real. Hence, the circle is a real circle.
2. If $\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}=0$, then the radius of the circle will be real $(=0)$. Hence, the circle is a Point circle because the radius is 0 .
3. If $\mathrm{g}^2+\mathrm{f}^2-\mathrm{c}<0$, then the radius of the circle will be imaginary. Hence, the circle is an imaginary circle.

Parametric Equation

To represent any point on a curve in terms of a single variable (parameter), we use parametric form of that curve.

1. Parametric Form for $x^2+y^2=r^2$

$P(x, y)$ is a point on the circle $x^2+y^2=r^2$ with centre $O(0,0)$. And $O P$ makes an angle $\theta$ with the positive direction of the $X$-axis, then $x=r \cdot \cos \theta$, $y=r \cdot \sin \theta$ called the parametric equation of the circle.
Here as $\theta$ varies, the point on the circle also changes, and thus $\theta$ is called the parameter. Here $0 \leq \theta<2 \pi$.
So any arbitrary point on this circle can be assumed as $(r \cdot \cos \theta, r \cdot \sin \theta)$

2. Parametric Form for $(x-h)^2+(y-k)^2=r^2$

Centre of the circle here is $(\mathrm{h}, \mathrm{k})$.
Parametric point on it is $(h+r \cdot \cos \theta, k+r \cdot \sin \theta)$.

Parabola

A parabola is the locus of a point moving in a plane such that its distance from a fixed point (focus) is equal to its distance from a fixed line (directrix).

$\begin{equation}
\text { Hence it is a conic section with eccentricity e }=1 \text {. }
\end{equation}$

$\begin{aligned} & \frac{P S}{P M}=e=1 \\ & \Rightarrow P S=P M\end{aligned}$

Standard equation of a parabola

If the directrix is parallel to the y-axis in the standard equation of a parabola is given as
$
y^2=4 a x
$
If the directrix is parallel to the $x$-axis, the standard equation of a parabola is given as

$
x^2=4 a y
$

Parametric Equation

From the equation of the parabola, we can write $\frac{y}{2 a}=\frac{2 x}{y}=t$ here, t is a parameter
Then, $x=a t^2$ and $y=2 a t$ are called the parametric equations and the point $\left(a t^2, 2 a t\right)$ lies on the parabola.

Point $\mathrm{P}(\mathrm{t})$ lying on the parabola means the coordinates of P are (at $\left.{ }^2, 2 a t\right)$

General Equation of Parabola

Let $S(h, k)$ be the focus and $\mathrm{l} x+m y+n=0$ be the equation of the directrix, and $\mathrm{P}(\mathrm{x}, \mathrm{y})$ be any point on the parabola.

Then, from the definition PS $=\mathrm{PM}$

$
\Rightarrow \quad \sqrt{(x-h)^2+(y-k)^2}=\left|\frac{l x+m y+n}{\sqrt{\left(l^2+m^2\right)}}\right|
$
Squaring both sides, we get

$
\Rightarrow \quad(x-h)^2+(y-k)^2=\frac{(l x+m y+n)^2}{\left(l^2+m^2\right)}
$
This is the general equation of a parabola.

Important Terms related to Parabola

Axis: The line that passes through the focus and is perpendicular to the Directrix of the parabola. For parabola $y^2=4 \mathrm{ax}_{\text {, }}$ the x -axis is the Axis.

Vertex: The point of intersection of the parabola and axis. For parabola $y^2=4 \mathbf{a x}$, $A(0,0)$ i.e. origin is the Vertex.

Double Ordinate: Suppose a line perpendicular to the axis of the parabola meets the curve at Q and $\mathrm{Q}^{\prime}$. Then, QQ ' is called the double ordinate of the parabola.

Latus Rectum: The double ordinate LL' passing through the focus is called the latus rectum of the parabola.

Focal Chord: A chord of a parabola which is passing through the focus. In the figure PP' and LL' are the focal chord.

Focal Distance: The distance from the focus to any point on the parabola.

Four Common Forms of a Parabola

Hyperbola

A Hyperbola is the set of all points ( $x, y$ ) in a plane such that the difference of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci).
Or,
The locus of a point moves in a plane such that the ratio of the distance from a fixed point (focus) to the distance from a fixed line (directrix) is constant. The constant is known as eccentricity e and for hyperbola $\mathrm{e}>1$.

Standard Equation of Hyperbola

The standard form of the equation of a hyperbola with centre $(0,0)$ and foci lying on the $x$-axis is $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \quad$

where, $b^2=a^2\left(e^2-1\right)$

Parametric Equation of Hyperbola

The equations $x=a \sec \theta, y=b \tan \theta$ are called the parametric equation of the hyperbola
The circle with centre $O(0,0)$ and $O A$ as the radius is called the auxiliary circle of the hyperbola.

Terms related to Hyperbola

Centre: All chord passing through point $O$ is bisected at point $O$. Here $O$ is the origin, i.e. $(0,0)$.

Foci: Point $S$ and $S^{\prime}$ are foci of the hyperbola where, $S$ is $(\mathrm{ae}, 0)$ and $S^{\prime}$ is $(-\mathrm{ae}, 0)$.

Directrices: The straight line ZM and Z'M' are two directrices of the hyperbola and their equations are $x=$ ae and $x=-a e$.

Double Ordinate: If a line perpendicular to the transverse axis of the hyperbola meets the curve at Q and Q', then QQ' is called double ordinate.

Latus rectum: Double ordinate passing through focus is called latus rectum. Here $L L^{\prime}$ and $L_1 L_1{ }^{\prime}$ are two latus rectum of a hyperbola.

Vertices: The points where the hyperbola intersects the axis are called the vertices. The vertices of the hyperbola are $(a, 0),(-a, 0)$.

Transverse Axis: The line passing through the two foci and the centre of the hyperbola is called the transverse axis of the hyperbola.

Conjugate Axis: The line passing through the centre of the hyperbola and perpendicular to the transverse axis is called the conjugate axis of the hyperbola.

Eccentricity of Hyperbola: $(\mathrm{e}>1)$ The eccentricity is the ratio of the distance of the focus from the centre of the hyperbola, and the distance of the vertex from the centre of the hyperbola.

Ellipse

An ellipse is the set of all points $(x, y)$ in a plane such that the sum of their distances from two fixed points is a constant. Each fixed point is called a focus (plural: foci).

OR

The locus of a point moves in a plane such that the ratio of the distance from a fixed point (focus) to the distance from a fixed line (directrix) is constant. The constant is known as eccentricity e and for ellipse $0 < e < 1$.

In geometry, an ellipse is a two-dimensional shape, that is defined along its axes. An ellipse is formed when a cone is intersected by a plane at an angle with respect to its base.

It has two focal points. The sum of the two distances to the focal point, for all the points in the curve, is always constant.

A circle is also an ellipse, where the foci are at the same point, which is the centre of the circle.

Standard Equation of Ellipse

The standard form of the equation of an ellipse with centre $(0,0)$ and major axis on the x-axis is $\frac{\mathrm{x}^2}{\mathbf{a}^2}+\frac{\mathbf{y}^2}{\mathbf{b}^2}=1 \quad$ where $\mathrm{b}^2=\mathrm{a}^2\left(1-\mathrm{e}^2\right)$
1. $a>b$
2. the length of the major axis is $2 a$
3. the length of the minor axis is $2 b$
4. the coordinates of the vertices are $( \pm a, 0)$

Important Terms related to ellipse

Centre: All chord passing through point $C$ is bisected at point $C$. Here $C$ is the origin, i.e. $(0, 0)$.

Foci: Point $S$ and $S’$ are foci of the ellipse where, $S$ is $(ae, 0)$ and $S’$ is $(-ae, 0)$.

Directrices: The straight-line $ ZM$ and $Z’M’$ are two directrices of the ellipse and their equations are $x = a/e$ and $x = -a/e$.

Axis: In Figure $AA’$ is called the major axis and $BB’$ is called the minor axis. $2a$ is called the length of the major axis and $2b$ is called the length of the minor axis.

Double Ordinate: If a line perpendicular to the major axis meets the curve at $P$ and $P’$, then $PP’$ is called double ordinate.

Latus rectum: Double ordinate passing through focus is called latus rectum. Here $LL’$ is a latus rectum. There is another latus rectum that passes through the other focus $S'$. So an ellipse has $2$ latus rectum

Parametric Equation of Ellipse

The equations $x=a \cos \theta, y=b \sin \theta$ are called the parametric equation of the ellipse.

The parametric equation of the ellipse is given by $x=a \cos \theta, y=b \sin \theta$ and the parametric coordinates of the points lying on it is ( $a \cos \theta, b \sin \theta)$.

Conic Sections Formulas

Conic section formulas class 11 include formulas on circle conic section, parabola conic section, hyperbola conic section and Ellipse conic section formulas.

Circle - Conic Section Formulas

Equation of the Tangent in Point Form

The equation of the tangent to a circle $x^2+y^2+2 g x+2 f y+c=0$ at the point $P\left(x_1, y_1\right)$ is $x_1+y_1+g\left(x+x_1\right)+f\left(y+y_1\right)+c=0$

Equation of Tangent of Circle in Parametric Form

The equation of the tangent at the point $(a \cos \theta, \mathrm{a} \sin \theta)$ to a circle $\mathrm{x}^2+\mathrm{y}^2=\mathrm{a}^2$ is $\mathrm{x} \cos \theta+\mathrm{y} \sin \theta=\mathbf{a}$

Equation of the Tangent in Slope Form

The equation of the tangent to a circle $\mathrm{x}^2+\mathrm{y}^2=\mathrm{a}^2$ having slope m is $\mathrm{y}=\mathrm{mx} \pm \mathrm{a} \sqrt{\left(\mathbf{1 + \mathbf { m } ^ { 2 } )}\right.}$, and point of tangency is $\left( \pm \frac{a m}{\sqrt{\left(1+m^2\right)}}, \mp \frac{a}{\sqrt{\left(1+m^2\right)}}\right)$.

Corollary: It also follows that $y=m x+c$ is tangent to $x^2+y^2=a^2$ if $c^2=a^2\left(1+m^2\right)$ which is the condition of tangency.

Point of Contact:

Solving $x^2+y^2=a^2$ and $y=m x \pm a \sqrt{1+m^2}$, simultaneously we get,

$\begin{aligned}
& x= \pm \frac{a m}{\sqrt{\left(1+m^2\right)}} \\
& y=\mp \frac{a}{\sqrt{\left(1+m^2\right)}}
\end{aligned}$

Thus, the coordinates of the points of contact are

$\left( \pm \frac{a m}{\sqrt{\left(1+m^2\right)}}, \mp \frac{a}{\sqrt{\left(1+m^2\right)}}\right)$

NOTE:
Equation of tangent of the circle $(x-h)^2+(y-k)^2=a^2$ in terms of slope is $(y-k)=m(x-h) \pm a \sqrt{\left(1+m^2\right)}$

Tangent from a Point to the Circle

• If a point lies outside of a circle (here point is P), then two tangents can be drawn from P to the circle. Here, PQ and PR are two tangents.

• If a point lies on the circle, then one tangent can be drawn from the point to the circle. If C is the point, then ACB is the tangent

• If a point lies inside the circle, then no tangent can be drawn from the point to the circle.

To get equation of the tangents from an external point

Circle is $: x^2+y^2=a^2$ and let the tangent to it be : $y=m x+a \sqrt{\left(1+m^2\right)}$
As the tangent passes through point $P\left(x_1, y_1\right)$ lying out side the circle then, $\mathrm{y}_1=\mathrm{mx}_1+\mathrm{a} \sqrt{\left(1+\mathrm{m}^2\right)}$

$\left(y_1-m x_1\right)^2=a^2\left(1+m^2\right)$

or, $\left(x_1^2-a^2\right) m^2-2 m x_1 y_1+y_1^2-a^2=0$
Which is quadratic equation in m which gives two value of m .

The tangents are real, imaginary or coincidence that is depends on the value of the discriminant.

If we have real values of m, then we can find the equations of 2 tangents using these slopes and the point P.

Length of tangent (PT) from a point to a circle

The length of the tangent from a point $\mathrm{P}\left(x_1, y_1\right)$ to the circle

$x^2+y^2+2 g x+2 f y+c=0 \text { is } \sqrt{x_1^2+y_1^2+2 g x_1+2 f y_1+c}$

Equation of Normal to a Circle

For a circle, the normal always passes through the centre of the circle.

Point Form:

The equation of the Normal at the point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ to a circle $\mathrm{S}=\mathrm{x}^2+\mathrm{y}^2+2 \mathrm{gx}+2 \mathrm{fy}+\mathrm{c}=0$ is $\frac{x-x_1}{g+x_1}=\frac{y-y_1}{f+y_1}$

Parabola - Conic Section Formula

Focal Distance Formula

The distance from the focus to any point on the parabola. i.e. PS

$
\begin{aligned}
& \mathrm{SP}=\mathrm{PM}=\text { Distance of } \mathrm{P} \text { from the directrix } \\
& \mathrm{P}=(x, y) \\
& \mathrm{SP}=\mathrm{PM}=\mathrm{x}+\mathrm{a}
\end{aligned}
$

Length of the Latus rectum

The length of the latus rectum of the parabola $y^2=4 ax$ is 4$a$.

Tangent to Parabola

A line that touches the parabola exactly at one point is called the Tangent to Parabola

Tangents of Parabola in Point Form

Equation of tangent to the parabola $y^2=4 a x$ at the point $P\left(x_1, y_1\right)$ is $\mathrm{yy}_1=2 \mathrm{a}\left(\mathrm{x}+\mathrm{x}_1\right)$

Tangents of Parabola in Parametric Form

The equation of tangent to the parabola $y^2=4 \mathrm{ax}$ at the point $\left(\mathrm{at}^2, 2 \mathrm{at}\right)$ is $t y=x+a t^2$

Tangents of Parabola in Slope Form

Equation of the tangent to the parabola $\mathrm{y}^2=4 \mathrm{ax}$ at the point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is $\mathrm{yy}_1=2 \mathrm{a}\left(\mathrm{x}+\mathrm{x}_1\right)$

Normal to Parabola

The line perpendicular to the tangent of the parabola at the point of contact is the normal of a parabola.

Point Form

The equation of the Normal at the point $P(x1,y1)$ to a Parabola $y2 = 4ax$ i $y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right)$

Normal in Parametric Form of Parabola

The equation of normal to the parabola $y^2=4{ax}$ at the point $\left({at}^2, 2{at}\right)$ is $y+t x=2 a t+a t^3$

Normal in Slope Form of Parabola

The equation of the Normal at the point $P(x1,y1)$ to a Parabola $y2=4ax$ is $y-y_1=-\frac{y_1}{2 a}\left(x-x_1\right)$

Hyperbola - Conic Section Formula

Eccentricity of Hyperbola

Equation of the hyperbola is $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ we have,

$
\begin{aligned}
& \mathrm{b}^2=\mathrm{a}^2\left(\mathrm{e}^2-1\right) \\
& \mathrm{e}^2=\frac{\mathrm{b}^2+\mathrm{a}^2}{\mathrm{a}^2} \\
& \mathrm{e}=\sqrt{1+\left(\frac{\mathrm{b}^2}{\mathrm{a}^2}\right)} \\
& \mathrm{e}=\sqrt{1+\left(\frac{2 \mathrm{~b}}{2 \mathrm{a}}\right)^2} \\
& \mathrm{e}=\sqrt{1+\left(\frac{\text { conjugate axis }}{\text { transverse axis }}\right)^2}
\end{aligned}
$

Focal Distance of a Point
The difference between the focal distance at any point of the hyperbola is constant and is equal to the length of the transverse axis of the hyperbola.

If $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ is any point on the hyperbola.

$
\begin{aligned}
& \mathrm{SP}=\mathrm{ePM}=e\left(x_1-\frac{a}{e}\right)=e x_1-a \\
& \mathrm{~S}^{\prime} \mathrm{P}=\mathrm{eP} \mathrm{M}=e\left(x_1+\frac{a}{e}\right)=e x_1+a \\
& \left|\mathrm{~S}^{\prime} \mathrm{P}-\mathrm{SP}\right|=\left|\mathrm{ex}_1+\mathrm{a}-\mathrm{ex}_1+\mathrm{a}\right|=2 \mathrm{a}
\end{aligned}
$

Equation of Asymptotes of Hyperbola

The equation of the asymptotes of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ are $y= \pm \frac{b}{a} x$ or $\frac{x}{a} \pm \frac{y}{b}=0$

Angle Between Asymptotes of Hyperbola

The angle between the asymptotes of the hyperbola $\frac{y^2}{a^2}-\frac{y^2}{b^2}=1$ is $2 \tan ^{-1}\left(\frac{b}{a}\right)$
If the angle between the asymptotes of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is $2 \theta$ then $e=\sec \theta$

Equation of Tangent of Hyperbola in Point Form

The equation of tangent to the hyperbola, $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ at point $\left(x_1, y_1\right)$ is $\frac{\mathrm{xx}_1}{\mathrm{a}^2}-\frac{\mathrm{yy}_1}{\mathrm{~b}^2}=1$

Equation of Tangent of Hyperbola in Parametric Form

The equation of tangent to the hyperbola, $\frac{\mathrm{x}^2}{\mathrm{a}^2}-\frac{\mathrm{y}^2}{\mathrm{~b}^2}=1$ at $(\mathrm{a} \sec \theta, \mathrm{b} \tan \theta)$ is $\frac{\mathrm{x}}{\mathrm{a}} \sec \theta-\frac{\mathrm{y}}{\mathrm{b}} \tan \theta=1

Equation of Normal of Hyperbola in Point form

The equation of normal to the hyperbola at $\left(x_1, y_1\right)$, $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is $\frac{a^2 x}{x_1}+\frac{b^2 y}{y_1}=a^2+b^2$

Equation of Normal of Hyperbola in Parametric form

The equation of normal at $(a \sec \theta, b \tan \theta)$ to the hyperbola, $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is $a x \cos \theta+b y \cot \theta=a^2+b^2$

Equation of Normal of Hyperbola in Slope form

The equation of normal of slope m to the hyperbola, $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ are $y=m x \mp \frac{m\left(a^2+b^2\right)}{\sqrt{a^2-m^2 b^2}}$ and coordinate of point of contact is $\left( \pm \frac{a^2}{\sqrt{a^2-m^2 b^2}}, \mp \frac{m b^2}{\sqrt{a^2-m^2 b^2}}\right)$

The equation of normal at $(a \sec \theta, b \tan \theta)$ to the hyperbola, $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ is $a x \cos \theta+b y \cot \theta=a^2+b^2$

Ellipse - Conic Sections

Eccentricity of the Ellipse

The ratio of distances from the centre of the ellipse from either focus to the semi-major axis of the ellipse is defined as the eccentricity of the ellipse. Theeccentricity of ellipse is $e=\sqrt{1-\frac{b^2}{a^2}}$.

Equation of Tangent of an Ellipse

For any point $\left(x_1, y_1\right)$ on the ellipse, the equation of the tangent to ellipse at that point is given by:

$
\frac{x_1 x}{a^2}+\frac{y_1 y}{b^2}=1
$

Normal at a point of an Ellipse

Normal at a point of the ellipse is a line perpendicular to the tangent and passing through the point of contact. The equation of normal at $\left(x_1, y_1\right)$ to the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is

$
\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2
$

Conic Sections in Real Life

Applications in various fields encompassing gears, vents in dams, wheels and circular geometry leading to trigonometry as application based on properties of circles; arches, dish, solar cookers, head-lights, suspension bridges, and searchlights as application based on properties of parabola; arches, Lithotripsy in the field of Medicine, whispering galleries, Ne-de-yag lasers and gears as application based on properties of ellipse; and telescopes, cooling towers, spotting locations of ships or aircrafts as application based on properties of hyperbola, to name a few.

List of Topics According to NCERT/JEE MAIN

Importance of Conic Section Class 11

Conic sections are widely used in various fields like Astronomy, Medicine, Architecture, Engineering, Physics, etc. The orbit of the solar system is in the shape of an ellipse. So, to study the characteristics of the orbit and related object, it is important to know about the properties of the ellipse. Similarly, curves like parabola and hyperbola play a major role in fields like Engineering and Architecture. It is also one of the important topics in JEE MAIN.

How to Study Conic Section Class 11?

Start preparing by understanding what is conic section. Try to be clear on concepts like the general equation of conic sections, and class 11 conic section formulas. Practice many problems from each topic for better understanding.

If you are preparing for competitive exams then solve as many problems as you can. Do not jump on the solution right away. Remember if your basics are clear you should be able to solve any question on this topic.

Important Books for Conic Sections

Start from NCERT Books, the illustration is simple and lucid. You should be able to understand most of the things. Solve all problems (including miscellaneous problems) of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the book Coordinate Geometry By SK Goyal. Conic Sections are explained very well in these books and there are an ample amount of questions with crystal clear concepts. Choice of reference book depends on person to person, find the book that best suits you the best, depending on how well you are clear with the concepts and the difficulty of the questions you require.

NCERT Solutions Subject-wise link:

• NCERT solutions for class 11 Physics.

• NCERT solutions for class 11 Chemistry.

• NCERT solutions for class 11 Mathematics.

• NCERT solutions for class 11 Biology.