Escribed Circle of Triangle: Definition & Meaning

Overview of a Triangle

A triangle is a polygon with three sides and three angles, making it the simplest polygon. Triangles are fundamental in geometry because many formulas, theorems, and properties are based on them. A triangle has six main elements: three sides and three angles, which are related through various rules such as the triangle inequality theorem, angle sum property, and trigonometric relations.

In a triangle $\triangle ABC$, the angles are denoted by $A$, $B$, and $C$, and the sides opposite these angles are denoted by $a$, $b$, and $c$ respectively:

For a triangle $\triangle ABC$, the following symbols and notations are universally adopted:

Angles: $\angle BAC = A, \quad \angle ABC = B, \quad \angle BCA = C$

Sides: $AB = c, \quad AC = b, \quad BC = a$

Semi-perimeter ($s$) and Perimeter:

$s = \frac{a+b+c}{2}, \quad \text{Perimeter } = 2s = a+b+c$

Area: The area of the triangle is denoted by $S$ or $\Delta$.

Basic Properties:

• Angle sum: $A + B + C = 180^\circ$

• Triangle inequality: $a + b > c, \quad b + c > a, \quad c + a > b$

• Positive side lengths: $a > 0, \quad b > 0, \quad c > 0$

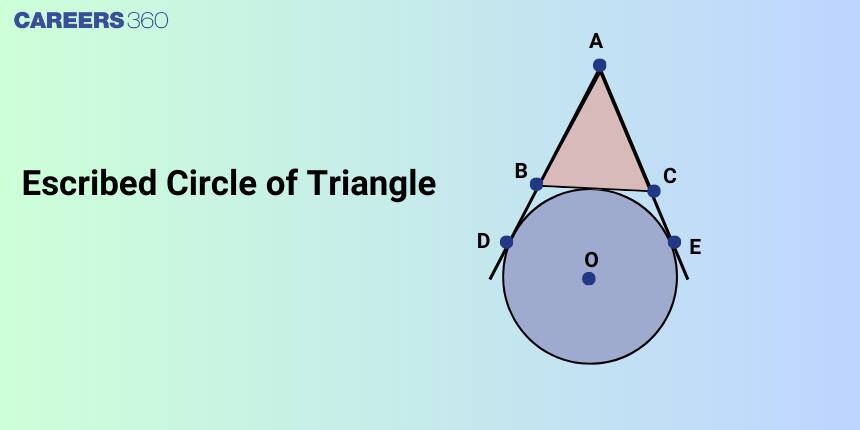
Escribed Circle of Triangle

The circle that touches the side $B C$ and two sides $A B$ and $A C$ produced of triangle $A B C$ is called the escribed circle opposite to the angle $A$. Its radius is denoted by $r_1$. Similarly, $r_2$ and $r_3$ denote the radii of the escribed circles opposite to the angles $B$ and $C$ respectively.

Formulae for $r_1, r_2$ and $r_3$,
1. $r_1=\frac{\Delta}{s-a}, \quad r_2=\frac{\Delta}{s-b}, \quad r_3=\frac{\Delta}{s-c}$
2. $r_1=s \tan \frac{A}{2}, \quad r_2=s \tan \frac{B}{2}, \quad r_3=s \tan \frac{C}{2}$
3. $r_1=4 R \sin \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}, \quad r_2=4 R \cos \frac{A}{2} \sin \frac{B}{2} \cos \frac{C}{2}, \quad r_3=4 R \cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}$

Difference Between Incircle and Excircle

• Incircle: Lies inside the triangle, touches all three sides, radius is $r$, centre is the incentre ($I$).

• Excircle: Lies outside the triangle, touches one side and the extensions of other two sides, radius is $r_\text{ex}$, centre is the excentre ($I_\text{ex}$).

Excentre of a Triangle

The excentre of a triangle is the point where two external angle bisectors and one internal angle bisector intersect. It serves as the centre of the escribed circle (excircle), and understanding its coordinates, properties, and relation to triangle sides is essential for solving triangle geometry problems and competitive exam questions.

Definition of Excentre

The excentre ($I_\text{ex}$) is the point of intersection of two external angle bisectors and one internal angle bisector of a triangle. There are three excentres in a triangle, one opposite each vertex.

Properties of Excentre

The distance from the excentre to the triangle sides gives the exradius:

$r_\text{ex} = \text{distance from } I_\text{ex} \text{ to a side of the triangle}$

Each excentre lies outside the triangle, opposite its corresponding vertex.

The triangle’s semiperimeter ($s$) and side lengths ($a, b, c$) relate to exradius $r_a, r_b, r_c$:

$r_a = \frac{\Delta}{s-a}, \quad r_b = \frac{\Delta}{s-b}, \quad r_c = \frac{\Delta}{s-c}$

where $\Delta$ is the area of the triangle.

Coordinates of Excentre in a Triangle

If vertices are $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$ and sides opposite them are $a$, $b$, $c$, the excentre opposite $A$ has coordinates:

$I_a = \left( \frac{-a x_1 + b x_2 + c x_3}{-a + b + c}, \frac{-a y_1 + b y_2 + c y_3}{-a + b + c} \right)$

Exradius of a Triangle

The exradius of a triangle is the radius of the escribed circle opposite a vertex. Knowing the exradius formulas, its relation with area and semi-perimeter, and how to calculate it helps in solving triangle geometry problems and applying excircle-related formulas effectively.

Formula for Exradius

The exradius ($r_\text{ex}$) is the radius of the escribed circle opposite a vertex. For triangle with area $\Delta$ and semiperimeter $s$, the exradius opposite side $a$ is:

$r_a = \frac{\Delta}{s-a}, \quad r_b = \frac{\Delta}{s-b}, \quad r_c = \frac{\Delta}{s-c}$

Relation Between Exradius, Area, and Semi-Perimeter

The triangle area can also be expressed in terms of exradius:

$\Delta = r_a (s-a) = r_b (s-b) = r_c (s-c)$

Trigonometric Formulas for Exradius

The exradius can be written using angles and circumradius $R$:

$r_a = 4R \sin\frac{A}{2} \sin\frac{B}{2} \sin\frac{C}{2} \cdot \csc^2 \frac{A}{2}$

Properties of Escribed Circle

The escribed circle of a triangle has unique properties, including tangency with one side and extensions of the other two sides. Understanding these properties, distances from excentre, and relations with incentre and circumcentre is important for solving triangle geometry problems accurately.

Tangency Properties with Triangle Sides

• The escribed circle touches one side of the triangle and the extensions of the other two sides.

• The distances from the excentre to points of tangency are equal to the exradius ($r_\text{ex}$): $I_a E = I_a F = I_a G = r_a$

Relation with Incentre and Circumcentre

• The incentre ($I$) lies inside the triangle, while the excentre ($I_a, I_b, I_c$) lies outside.

• Excentres, incentre, and circumcentre form important collinearities in triangle geometry.

Construction of Escribed Circle

The construction of an escribed circle involves locating the excentre and drawing a circle tangent to one side of the triangle and the extensions of the other two sides. Learning this geometric construction step-by-step helps in visualizing triangle properties and applying excircle formulas effectively.

Geometric Construction Using Compass and Straightedge

1. Draw triangle $ABC$ and extend its sides as needed.

2. Construct the internal angle bisector for one vertex and external bisectors for the other two vertices.

3. The intersection point is the excentre ($I_a$).

Step-by-Step Method

1. Identify the vertex opposite which you want the excircle.

2. Draw external bisectors of the other two angles.

3. Measure perpendicular distance from $I_a$ to the chosen side; this is the exradius $r_a$.

4. Draw a circle centered at $I_a$ with radius $r_a$ to complete the escribed circle.

Important Formulas Related to Excircle

This section covers the important formulas related to the excircle of a triangle, including exradius, area, semiperimeter, and coordinates of excentre. Knowing these formulas is essential for solving triangle geometry problems and applying excircle properties in exams.

Exradius in Terms of Sides and Area

$r_a = \frac{\Delta}{s-a}, \quad r_b = \frac{\Delta}{s-b}, \quad r_c = \frac{\Delta}{s-c}$

Trigonometric Relations for Exradius

$r_a = 4R \sin\frac{A}{2} \sin\frac{B}{2} \sin\frac{C}{2} \cdot \csc^2 \frac{A}{2}$

Coordinates of Excentre

For vertices $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$ and sides $a$, $b$, $c$, excentre opposite $A$ is:

$I_a = \left( \frac{-a x_1 + b x_2 + c x_3}{-a + b + c}, \frac{-a y_1 + b y_2 + c y_3}{-a + b + c} \right)$

Solved Examples Based on Escribed Circle of Triangle

Example 1: Find the value of $\frac{r_1+r_2+r_3-r}{2 R}$ where $r_1, r_2, r_3$ are radii of ex-circles and $r$ and $R$ is the radii of the incentre and circumcentre

1) $0$y

2) $1$

3) $2$

4) $4$

Solution:

$\begin{aligned} & r_1+r_2+r_3-r=\frac{\Delta}{(s-a)}+\frac{\Delta}{(s-b)}+\frac{\Delta}{(s-c)}-\frac{\Delta}{(s)} \\ & =\Delta\left[\frac{s-b+s-a}{(s-a)(s-b)}+\frac{(s-s+c)}{(s)(s-c)}\right] \\ & =\Delta\left[\frac{c}{(s-a)(s-b)}+\frac{(c)}{(s)(s-c)}\right] \\ & =\Delta c\left[\frac{s(s-c)+(s-a)(s-b)}{s(s-a)(s-b)(s-c)}\right] \\ & =\Delta c\left[\frac{\left.2 s^2-s(a+b+c)+a b\right)}{\Delta^2}\right] \\ & =\frac{c}{\Delta}(a b) \\ & =\frac{a b c}{\Delta} \\ & =4 R \\ & \Rightarrow \frac{r_1+r_2+r_3-r}{2 R}=2\end{aligned}$

Hence, the answer is the option (3).

Example 2: In triangle $\mathrm{ABC}$ if $r_1, r_2, r_3$ are radii of ex-circles and $r_2=r_1+r_3+r$ then which of following is true?

1) $A$ is a acute angle

2) $B $ is a right angle

3) $C$ is a acute angle

4) All of above

Solution:

$\begin{aligned} & r_2=r_1+r_3+r \\ & r_2-r=r_1+r_3 \\ & \frac{\Delta}{(s-b)}-\frac{\Delta}{(s)}=\frac{\Delta}{(s-a)}+\frac{\Delta}{(s-c)} \\ & \frac{\Delta b}{s(s-b)}=\frac{\Delta(2 s-a-c)}{(s-a)(s-c)} \\ & s(s-b)=(s-a)(s-c) \\ & s^2-s b=s^2-s(a+c)+a c \\ & s(a+c-b)=a c \\ & (a+b+c)(a+c-b)=2 a c \\ & (a+c)^2-b^2=2 a c \\ & a^2+c^2=b^2\end{aligned}$

Hence, it is a right-angled triangle with a right angle at $B$.

Hence, the answer is the option (4).

Example 3: In a triangle with sides $a, b, c, r_1>r_2>r_3$ (which are the ex-radii) then:
1) $a>b>c$
2) $a<b<c$
3) $a>b$ and $b<c$
4) $a<b$ and $b>c$

Solution:

The ex-radii of a triangle are given by

$r_1=\frac{\Delta}{s-a} r_2=\frac{\Delta}{s-b} r_3=\frac{\Delta}{s-c}$

where, $r_1, r_2$, and $r_3$ are the ex-radii of the triangle for the ex-circles in front of vertices $A, B$, and $C$ respectively.

$\begin{aligned}
& r_1>r_2>r_3 \\
\Rightarrow & \frac{\Delta}{s-a}>\frac{\Delta}{s-b}>\frac{\Delta}{s-c}
\end{aligned}$

Now, as $\Rightarrow s-a<s-b<s-c$

$\Rightarrow a>b>c$

Hence, the answer is the option (1).

Example 4: If $I_1, I_2, I_3$ are the centers of escribed circles of $\triangle A B C$, the the area of the triangle $I_1, I_2, I_3$ is
1) 1
2) -1
3) $\frac{a b c}{2 r}$
4) $-\frac{a b c}{2 r}$

Solution:

$I_1, I_2, I_3$ are the centers of escribed circles of $\triangle ABC$

$\text{Area} = \frac{I_1 I_2 \times I_2 I_3 \times I_1 I_3}{4R}$

Applying the formula:

$\text{Area} = \frac{(4R \cos \frac{A}{2}) \times (4R \cos \frac{B}{2}) \times (4R \cos \frac{C}{2})}{2 \times 4R}$
$\text{Area} = 8 R^2 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}$
$\text{Area} = \frac{8 R^2 \sin A \sin B \sin C}{8 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}}$
$\text{Area} = \frac{R^2 a b c}{8 R^3 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}}$
$\text{Area} = \frac{a b c}{2 (4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2})}$
$\text{Area} = \frac{a b c}{2 r}$

Hence, the correct answer is option 3.

List of Topics Related to the Escribed circle of a triangle

Explore the key topics related to the escribed circle of a triangle, including excentres, triangle properties, and important formulas. Understanding these topics helps in mastering triangle geometry and solving related exam questions efficiently.

NCERT Resources

Explore the NCERT resources for Chapter 3 – Trigonometric Functions, including Class 11 Maths notes, step-by-step solutions, and exemplar problems. These resources help students understand concepts clearly, practice effectively, and improve performance in exams.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3- Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3- Trigonometric Functions

Practice Questions based on the Escribed circle of a triangle

Practice these questions on the escribed circle of a triangle to strengthen your understanding of triangle properties, excentres, and related geometry formulas. These problems help improve accuracy and exam preparation.

Escribed Circle Of Triangle - Practice Question MCQ

You can practice the related questions from the links shared below: