How to Find Area of Triangle: Formulas and Examples

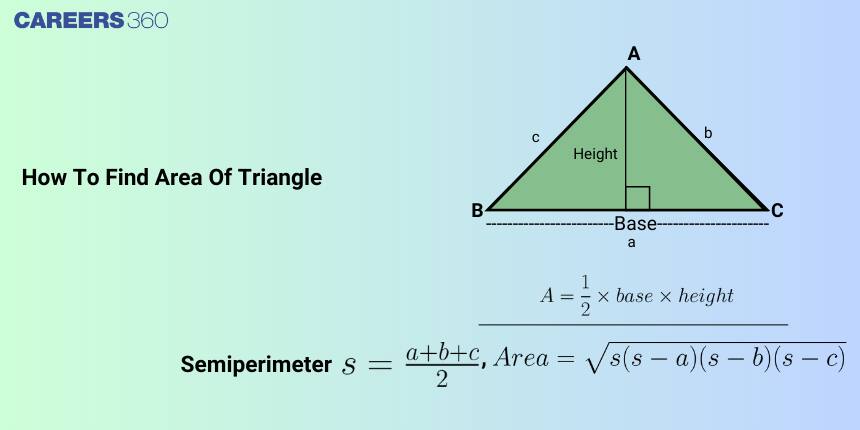
What is the Area of the Triangle?

The area of a triangle is the region enclosed by the three sides of the triangle. There are many methods by which we can find the area of a triangle such as if the base and height of the triangle are given or three sides of a triangle are given or two sides and an angle enclosed between them is given.

The area of a triangle is usually denoted by $Δ$ or $S$. There are many different formulas to find the area of the triangle.

Area of Triangle Using Base and Height

When the base and height of a triangle are known, the area can be calculated quickly. This is one of the most basic and commonly used methods when learning how to find area of triangle.

Formula to Calculate Area of Triangle ($A = \tfrac{1}{2} \times base \times height$)

The formula to calculate area of triangle using base and height is:
$A = \tfrac{1}{2} \times base \times height$

Here, the base is the side chosen as the reference line, and the height is the perpendicular drawn from the opposite vertex to this base. This formula is widely used in geometry and helps in school-level problems as well as real-life applications like land measurement.

How to find the area of a triangle?

Finding the area of a triangle can be done in several ways, such as using base and height, Heron’s formula, trigonometry, or coordinates. These formulas help you calculate the area of a triangle with 3 sides or a right triangle easily. In this section, we explain all these methods clearly.

Area of an Equilateral Triangle

An equilateral triangle is a triangle in which all three sides are equal. When a perpendicular is drawn from a vertex to the opposite side, it bisects the base, forming two congruent right triangles.

The area of an equilateral triangle is given by:

$A = \frac{\sqrt{3}}{4} \cdot \text{side}^2$

This formula is useful for quickly calculating the area when all sides are equal without needing to find the height separately.

Area of an Isosceles Triangle

An isosceles triangle has two equal sides, and the angles opposite these sides are also equal. The perpendicular from the vertex opposite the base divides the base into two equal halves.

The area of an isosceles triangle can be calculated as:

$A = \frac{1}{2} \cdot \sqrt{a^2 - \frac{b^2}{4}} \cdot b$

Here, $a$ is the length of the equal sides, and $b$ is the base. This formula uses the Pythagorean theorem to find the height and then applies the standard $A = \frac{1}{2} \cdot \text{base} \cdot \text{height}$ formula.

Area of a Triangle Given Two Sides and the Included Angle (SAS)

If two sides and the included angle are known, the area of a triangle can be calculated using trigonometry.

The height can be expressed as:
$h = c \cdot \sin A$

The general formula for the area using base and height is:
$A = \frac{1}{2} \times \text{base} \times \text{height}$

For triangle $ABC$ with sides $a, b, c$ and angle $A$ between sides $b$ and $c$:
$A = \frac{1}{2} \times BC \times AD = \frac{1}{2} \cdot b \cdot c \cdot \sin A$

Similarly, the area can be expressed using other sides and included angles:

$\Delta ABC = \frac{1}{2} b \cdot c \cdot \sin A = \frac{1}{2} a \cdot b \cdot \sin C = \frac{1}{2} c \cdot a \cdot \sin B$

Area of a Triangle Using Semiperimeter and Inradius

If $s$ is the semiperimeter of the triangle, $s = \frac{a+b+c}{2}$, and $r$ is the inradius, then the area of the triangle is given by:

$A = \Delta = r \cdot s$

This formula is useful in problems involving the inscribed circle of a triangle.

How to Find Area of Right Triangle

In a right triangle, one side is taken as the base and the other perpendicular side is the height. So, the area of right triangle can be found using the same formula:
$A = \tfrac{1}{2} \times base \times height$

For example, if the two perpendicular sides of a right triangle are 6 cm and 8 cm, then
$A = \tfrac{1}{2} \times 6 \times 8 = 24 , cm^2$

This method is simple and is often the fastest way when working with right-angled triangles.

Derivation Using Half-Angle Formula

Using the trigonometric formula for the area:
$A = \frac{1}{2} b \cdot c \cdot \sin A = \frac{1}{2} b \cdot c \cdot 2 \sin \frac{A}{2} \cos \frac{A}{2}$

Applying half-angle formulas:

$A = \frac{1}{2} \cdot b \cdot c \cdot \sqrt{\frac{(s-b)(s-c)}{b c}} \cdot \sqrt{\frac{s(s-a)}{b c}} = \sqrt{s(s-a)(s-b)(s-c)}$

This derivation connects Heron’s formula with trigonometry and half-angle identities, providing a deeper understanding of how the area formula works for any triangle.

Area of Triangle Using Heron’s Formula

When the three sides of a triangle are known, area of triangle using Heron’s formula becomes the most effective method. It is especially useful when height is not given or is difficult to calculate.

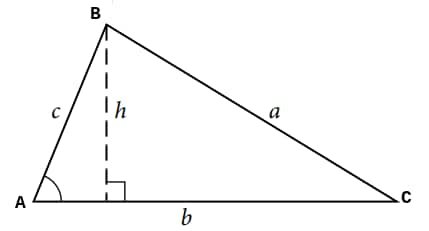
Step-by-Step Formula Derivation

Heron’s formula states that:

$A = \sqrt{s(s-a)(s-b)(s-c)}$

where $a, b, c$ are the sides of the triangle, and $s$ is the semiperimeter:
$s = \tfrac{a+b+c}{2}$

This method directly gives the area of triangle with 3 sides, without needing base and height.

How to Find Area of Triangle with 3 Sides

Suppose a triangle has sides $a=7$, $b=8$, $c=9$.
Then, $s = \tfrac{7+8+9}{2} = 12$.

Now,
$A = \sqrt{12(12-7)(12-8)(12-9)}$
$A = \sqrt{12 \times 5 \times 4 \times 3}$
$A = \sqrt{720} = 26.83 , cm^2$

This shows how Heron’s formula for the area of a triangle works in practice.

Area of a Triangle Using Coordinates

The area of a triangle using coordinates helps find the triangle’s area when the vertices are known. It is an important method alongside Heron’s formula and base-height formulas. Below are the key formulas and steps:

Formula to Calculate the Area of a Triangle with Coordinates

For a triangle with vertices $A(x_1, y_1)$, $B(x_2, y_2)$, and $C(x_3, y_3)$, the area of the triangle can be calculated using:
$A = \frac{1}{2} \left| x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y_1-y_2) \right|$

Area of a Triangle Using the Determinant Method

The determinant method provides a compact way to calculate area:
$A = \frac{1}{2} \left| \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{vmatrix} \right|$

Area of a Triangle Using Trigonometry

The area of a triangle using trigonometric functions is calculated when two sides and the included angle are known. This method complements base-height and Heron’s formula approaches. Below are the key formulas and examples:

If two sides $a$ and $b$ and the included angle $C$ are known, the area is:
$A = \frac{1}{2} a b \sin C$

Area of Triangle with Two Sides and an Included Angle

This method is also called the SAS (Side-Angle-Side) formula and works for any triangle where two sides and the included angle are given.

Uses in Advanced Geometry and Trigonometry

The trigonometric approach helps in solving triangle problems, finding heights, and connecting side lengths with angles.

Comparison of Different Methods to Find Area of Triangle

A comparison of different methods to find the area of a triangle helps choose the best approach for a given problem, whether using base-height, Heron’s formula, trigonometry, or coordinates. Below is a summary of the methods:

Choosing the Right Formula Based on Given Information

• Use base-height formula when height is easily known.

• Use Heron’s formula when all three sides are given.

• Use coordinate formulas when vertices are in a plane.

• Use trigonometric formulas when two sides and an included angle are known.

This helps in efficient calculation of triangle area depending on available data.

Solved Examples Based on the Area of Triangle

Example 1: If in a triangle $\mathrm{ABC}, A B=5$ units, $\angle \mathrm{B}=\cos ^{-1}\left(\frac{3}{5}\right)$ and the radius of the circumcircle of $\triangle A B C$ is $5$ units, then the area (in sq. units) of $\triangle A B C$ is [JEE MAINS 2021]

Solution:

Given, $A B=c=5, R=5$

$
B=\cos ^{-1}\left(\frac{3}{5}\right) \Rightarrow \cos B=\frac{3}{5} \Rightarrow \sin B=\frac{4}{5}
$

We know,

$
\frac{b}{\sin B}=2 R \Rightarrow b=2 R \sin B=2 \cdot 5 \cdot \frac{4}{5}=8
$

Using cosine rule.

$
\begin{aligned}
& \cos B=\frac{a^2+c^2-b^2}{2 a c} \\
& \frac{3}{5}=\frac{a^2+25-64}{2 \cdot a \cdot 5} \\
& \Rightarrow a^2-6 a-39=0 \\
& \Rightarrow a=\frac{6+8 \sqrt{3}}{2}=3+4 \sqrt{3} .
\end{aligned}
$

Now Area

$
=6+8 \sqrt{3}
$

Hence, the correct answer is $6+8 \sqrt{3}$

Example 2: In triangle $ \mathrm{ABC}$ ratio of sides $a:b:c=3:4:5$ and it has an incircle which has a center at $ \mathrm{O}$ then find the ratio of the area of $\triangle A O B: \triangle B O C: \triangle C O A $

Solution:

The area formula for a triangle is given as Area $=1 / 2$ bh, where ' $b$ ' is base and ' $h$ ' is the height. For oblique triangles, we must find ' $h$ ' before we can use the area formula.

$
\begin{aligned}
\text { Area } & =\frac{1}{2} \text { base } \times \text { height } \\
& =\frac{1}{2} b \cdot c \sin \mathrm{A}
\end{aligned}
$

Area of triangle $A B C$ is represented by $\Delta$, Thus

Area of $\triangle \mathrm{ABC}=\Delta =\frac{1}{2} b \cdot \mathrm{c} \sin \mathrm{A}
=\frac{1}{2} a \cdot \mathrm{b} \sin \mathrm{C}
=\frac{1}{2} c \cdot \mathrm{a} \sin \mathrm{B}$
NOTE:
Area of the triangle in terms of sides (Heron's Formula)

$
\Delta=\frac{1}{2} b \cdot \mathrm{c} \sin \mathrm{A}=\frac{1}{2} b c \cdot 2 \sin \frac{\mathrm{A}}{2} \cos \frac{\mathrm{A}}{2}
$

use half angle formula

$
\begin{aligned}
& =\frac{1}{2} \sqrt{\frac{(s-b)(s-c)}{b c}} \sqrt{\frac{s(s-a)}{b c}} \\
& =\sqrt{s(s-a)(s-b)(s-c)}
\end{aligned}
$

From the above Diagram, we can see

$
\begin{aligned}
& \Delta A O B: \triangle B O C: \triangle C O A=\frac{1}{2} \times 3 k \times r: \frac{1}{2} \times 4 k \times r: \frac{1}{2} \times 5 k \times r \\
= & 3: 4: 5
\end{aligned}
$

Hence, the answer is $3: 4: 5$

Example 3: In a triangle, $\mathrm{ABC} \frac{4 b^2 c^2-(a+b+c)(b+c-a)(a-b+c)(a+b-c)}{8 b^2 c^2}$ is equal to.
Solution:

$
\begin{aligned}
& \frac{4 b^2 c^2-(a+b+c)(b+c-a)(a-b+c)(a+b-c)}{8 b^2 c^2} \\
& =\frac{1}{2}-\frac{(a+b+c)(b+c-a)(a-b+c)(a+b-c)}{8 b^2 c^2} \\
& =\frac{1}{2}-\frac{2 s \times 2 \times(s-a) \times 2 \times(s-b) \times 2 \times(s-c)}{8 b^2 c^2} \\
& =\frac{1}{2}-\frac{2 s \times(s-a) \times(s-b) \times(s-c)}{b^2 c^2} \\
& =\frac{1}{2}-\frac{2 \Delta^2}{b^2 c^2} \\
& =\frac{1}{2}-\frac{2\left(\frac{1}{2} b c \sin A\right)^2}{b^2 c^2} \\
& =\frac{1}{2} \cos ^2 A
\end{aligned}
$

Hence, the answer is $\frac{1}{2} \cos ^2 A$

Example 4:If the sides of a triangle are the roots of the equation $x^3-4 x^2+5 x-2=0$, then the area of this triangle.
Solution:

$
\begin{aligned}
& x^3-4 x^2+5 x-2=0 \\
& (x-2)\left(x^2-2 x+1\right)=0 \\
& (x-2)(x-1)^2=0 \\
& a=2, b=1, c=1
\end{aligned}
$

As $b+c=a$, it is not a triangle, and the vertices are lying on a line
So, area $=0$
Hence, the answer is 0

Example 5: If in a $\triangle A B C$, the altitudes from the vertices $A, B, C$ on opposite sides are in H .P, then $\sin A, \sin B, \sin C$ are in:

Solution: Let the altitudes be $A D, B E$, and $C F$.
Now, the Area of the triangle $=\frac{1}{2}($ Base $)($ Height $)$
So $\frac{1}{2}(A B)(C F)=\frac{1}{2}(B C)(A D)=\frac{1}{2}(A C)(B E)=k($ say $)$
$A D=$ $ha$ altitude from $a$
then $\quad \frac{1}{2} a h a=\frac{1}{2} b h b=\frac{1}{2} c h c$
Thus $a=\frac{k}{h a}, b=\frac{k}{h b}, c=\frac{k}{h c}$

when k= is some constant --------(1)

Now $h a, h b, h c$ in HP

$
\Rightarrow \frac{2}{h b}=\frac{1}{h a}+\frac{1}{h c}----(2)
$

(1) and (2) we get

$
\begin{aligned}
& 2 b=a+c, \text { here } \\
& =A \cdot P
\end{aligned}
$

Hence, the answer is $\sin A, \sin B, \sin C$ are in the AP

List of Topics related to the Area of a triangle

Here is a list of important topics related to the area of a triangle, covering key formulas, methods, and concepts that simplify solving geometry problems.

NCERT Resources

For a clear understanding of trigonometric functions and triangle problems, NCERT Class 11 Maths Notes, Solutions, and Exemplar for Chapter 3 are very helpful. Below are the NCERT resources:

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3 - Trigonometric Functions

Practice Questions based on Area of triangle

You can practice questions based on the area of a triangle and related topics like simultaneous trigonometric equations, law of sines, law of tangents, projection formula, and semiperimeter and half-angle formulae.

Area Of Triangle - Practice Question MCQ

You can practice the related questions from the links shared below: