Trigonometric Equation using Minimum and Maximum value of Function
Trigonometric equations often require finding the minimum and maximum values of trigonometric functions, which is an important concept in Class 11 trigonometry and competitive exams. By using the trigonometry maximum and minimum values formula, students can easily solve questions involving $\sin \theta$, $\cos \theta$, and other functions. Understanding the maximum value of trigonometric functions and the minimum value of trigonometric equations helps in solving a wide range of problems. In this article, we will cover the formulas, key concepts, and practice questions related to the trigonometric equation using minimum and maximum value of function in mathematics.
This Story also Contains
- What are Trigonometric Equations?
- Maximum and Minimum Values of Trigonometric Equations
- Trigonometric Equation using Minimum and Maximum values of Trigonometric Functions
- Standard Formulas for Maximum and Minimum Values in Trigonometry
- Graphical Approach to Maximum and Minimum Values
- Solved Examples Based on Trigonometric Equations using Minimum and Maximum values of Function
- List of Topics Related to the Trigonometric Equation using Minimum and Maximum value of Function
- NCERT Resources
- Practice Questions on Trigonometric Equation using Minimum and Maximum Value of Function
What are Trigonometric Equations?
Trigonometric equations are equations that involve trigonometric functions like $\sin \theta$, $\cos \theta$, or $\tan \theta$. These equations are satisfied only for certain values of the unknown angle. A value of the angle that makes the equation true is called a solution or root of the equation.
For example, the equation $2 \sin x = 1$ is satisfied when $x = \pi/6$ between $0$ and $\pi$. The solutions of a trigonometric equation lying within a specific interval are often called principal solutions.
Solution of Trigonometric Equation
The solution of a trigonometric equation refers to the value of the unknown angle that satisfies the equation.
Example:
If $2 \sin \theta = 1$, then $\theta = 30^\circ$ is a solution. Because of the periodic nature of trigonometric functions, this equation has infinitely many solutions such as $(360+30)^\circ, (720+30)^\circ, (-360+30)^\circ$, and so on.
Principal Solution of Trigonometric Equations
The principal solutions of a trigonometric equation are those lying in the interval $[0, 2\pi)$.
Example: If $2 \sin \theta = 1$, then within $[0, 2\pi)$, the two solutions are $\pi/6$ and $5\pi/6$.
General Solution of Trigonometric Equations
Since trigonometric functions are periodic, solutions keep repeating within each period. The complete set of all possible solutions is called the general solution. This captures the infinite family of solutions for the given trigonometric equation.
Maximum and Minimum Values of Trigonometric Equations
The maximum and minimum values of trigonometric functions depend directly on the range of each function.
The minimum value is the lowest point in the function’s range.
The maximum value is the highest point in the function’s range.
Understanding the trigonometry maximum and minimum values formula is essential for solving higher-level problems, especially in Class 11 trigonometry and competitive exams.
Maximum and Minimum Value of Standard Trigonometric Functions
| Trigonometric Ratio | Maximum Value | Minimum Value |
|---|---|---|
| $\sin \theta$ | $1$ | $-1$ |
| $\cos \theta$ | $1$ | $-1$ |
| $\tan \theta$ | $\infty$ | $-\infty$ |
| $\cot \theta$ | $\infty$ | $-\infty$ |
| $\sec \theta$ | $\infty$ | $-\infty$ |
| $\csc \theta$ | $\infty$ | $-\infty$ |
Trigonometric Equation using Minimum and Maximum values of Trigonometric Functions
Sometimes, the maximum and minimum values of trigonometric functions are used to solve trigonometric equations.
While solving equations of the type $f(x) = g(x)$ with $x \in A$, we may encounter a situation such as:
If $f(x) \leq a$ and $g(x) \geq a$, then the only possibility for $f(x) = g(x)$ is when both are equal to $a$.
Steps to Solve Trigonometric Equations Using Maximum and Minimum Values
Find the maximum or minimum value of the trigonometric expression.
Check the condition under which the trigonometric function attains that value.
Use this condition to solve for the variable.
Illustration 1
If $3 \sin(ax) + 4 \cos(x) = 7$, find the possible values of $a$.
Here, maximum value of LHS is $7$ (since $3+4=7$), which occurs when $\sin(ax) = 1$ and $\cos(x) = 1$.
So, the equation holds only when:
$ax = (4n+1)\frac{\pi}{2}$
$x = 2m\pi, \quad n,m \in \mathbb{Z}$
$\frac{(4n+1)\pi}{2a} = 2m\pi$
$a = \frac{(4n+1)}{4m}, \quad n,m \in \mathbb{Z}$
Illustration 2
Solve $\sin(x) + \cos(x) = 2$.
The maximum value of $\sin(x) + \cos(x)$ is $2$, which occurs only when $\sin(x) = 1$ and $\cos(x) = 1$ simultaneously.
But, when $\sin(x) = 1$, $\cos(x) = 0$, not $1$.
Hence, no $x$ exists that satisfies both $\sin(x) = 1$ and $\cos(x) = 1$ at the same time.
Therefore, the equation $\sin(x) + \cos(x) = 2$ has no solution.
Standard Formulas for Maximum and Minimum Values in Trigonometry
Standard formulas for maximum and minimum values in trigonometry help quickly find the highest and lowest points of trigonometric expressions, essential for solving problems efficiently in exams and math practice.
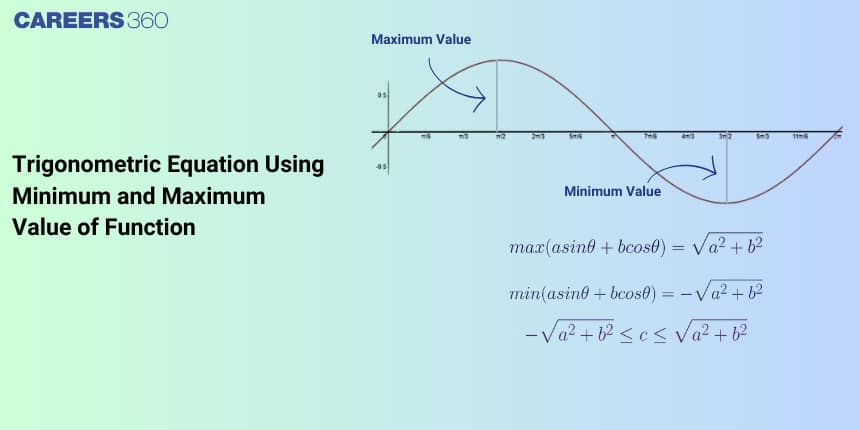
Formula for $a \sin \theta + b \cos \theta$
One of the most widely used trigonometric forms is $a \sin \theta + b \cos \theta$, which appears in competitive exams and board-level problems. By rewriting it as $r \sin(\theta + \alpha)$, where $r = \sqrt{a^2 + b^2}$ and $\tan \alpha = \tfrac{b}{a}$, its maximum and minimum values can be determined easily.
Maximum value of $a \sin \theta + b \cos \theta$ is $+\sqrt{a^2 + b^2}$.
Minimum value of $a \sin \theta + b \cos \theta$ is $-\sqrt{a^2 + b^2}$.
It can also be applied in word problems, vector projections, and harmonic analysis.
Formula for $\sin^2 \theta + \cos^2 \theta$ and variations
The fundamental identity $\sin^2 \theta + \cos^2 \theta = 1$ is the backbone of trigonometry. Many maximum and minimum problems extend this to weighted forms like $a \sin^2 \theta + b \cos^2 \theta$. The range of such expressions depends directly on the coefficients $a$ and $b$.
General range is between $\min(a,b)$ and $\max(a,b)$.
Example: $5 \sin^2 \theta + 2 \cos^2 \theta$ will always lie in $[2,5]$.
Similarly, $a \cos^2 \theta + b \sin^2 \theta$ has its values restricted between $a$ and $b$.
Such questions test both algebraic manipulation and conceptual clarity of trigonometric identities.
Quadratic trigonometric forms and their range
More complex questions involve quadratic trigonometric expressions such as $p \sin^2 \theta + q \sin \theta \cos \theta + r \cos^2 \theta$. These forms can be reduced using identities, substitution, or auxiliary angle methods to find the range.
Often converted into a quadratic in $\sin \theta$ or $\cos \theta$ for solving.
Completing the square helps in identifying maximum and minimum values quickly.
Graphical Approach to Maximum and Minimum Values
Below is a list of key points and practice insights to help understand the graphical approach to maximum and minimum values of trigonometric functions. This approach makes it easier to identify peaks, troughs, and ranges of $\sin \theta$, $\cos \theta$, $\tan \theta$, and other functions for solving problems efficiently.
Graph of $\sin \theta$ and $\cos \theta$ for range identification
The graphs of $\sin \theta$ and $\cos \theta$ are periodic functions that repeat every $2\pi$ radians. By observing the peaks and troughs of these graphs, we can quickly identify their maximum and minimum values.
Maximum value of $\sin \theta$ and $\cos \theta$: $+1$
Minimum value of $\sin \theta$ and $\cos \theta$: $-1$
Graphical visualization helps in understanding how these functions behave over an interval, making it easier to solve maximum and minimum values of trigonometric functions and related problems efficiently.
Behavior of $\tan \theta$, $\cot \theta$, $\sec \theta$, and $\csc \theta$
Unlike sine and cosine, $\tan \theta$ and $\cot \theta$ have vertical asymptotes where the function is undefined. Similarly, $\sec \theta$ and $\csc \theta$ diverge near their asymptotes. Graphing these functions allows us to:
Determine the intervals where the function exists
Identify local maximum and minimum values within a period
Understand the effect of periodicity and discontinuity on trigonometric equation using minimum and maximum value of function problems.
Solved Examples Based on Trigonometric Equations using Minimum and Maximum values of Function
Example 1:If $\cos ^2 \theta_1+\cos ^2 \theta_2+\cos ^2 \theta_3=0$, then which of the following is the possible value of $\sin \theta_1$ $+\sin \theta_2+\sin \theta_3$
1) $3$
2) $-3$
3) $-1$
4) All of above
Solution:
$\cos^2 \theta_1 + \cos^2 \theta_2 + \cos^2 \theta_3 = 0$
$\theta_1 = \theta_2 = \theta_3 = \pm \frac{\pi}{2}$
So, possible values of $\sin \theta_1 + \sin \theta_2 + \sin \theta_3$ are $\{-3, 3, 1, -1\}$
Hence, the answer is the option 4.
Example 2: Find the minimum value of $12 \cos ^2 \theta+3 \tan ^2 \theta$.
Solution:
$12 \cos ^2 \theta+3 \tan ^2 \theta=12 \cos ^2 \theta+3\left(\sec ^2 \theta-1\right)$
$=12 \cos ^2 \theta+3 \sec ^2 \theta-3$
Minimum value of $a \cos ^2 \theta+b \sec ^2 \theta=2 \sqrt{a b}, b \leq a$
$=2 \sqrt{36}-3$
$=12-3 =9$
Example 3: How many roots of equation $x \cos x=1$ are possible?
Solution: Trigonometric Equation using Minimum and Maximum value of Function
Sometimes, we use the maximum and minimum values of trigonometric functions to solve trigonometric equations.
While solving equations of the type $f(x) = g(x)$, and $x \in A$, we may come across the situation like:
If $x \in A$, $f(x) \leq a$ and $g(x) \geq a$, then $f(x) = g(x) = a$.
$x \cos x = 1$
$\cos x = \frac{1}{x} = y$
$\text{As } x \to \infty, \; y \to 0^{+}$
$\text{As } x \to -\infty, \; y \to 0^{-}$
The graph is given by:

By graph, we can say that it has infinitely many solutions
Hence the answer is infinite.
Example 4: Find the minimum value of $16 \sec ^2 \Theta+9 \csc ^2 \Theta+2$.
Solution: Minimum value of
$a \sec^2 \Theta + b \csc^2 \Theta = (\sqrt{a} + \sqrt{b})^2$
Minimum value of $16 \sec^2 \Theta + 9 \csc^2 \Theta = (\sqrt{16} + \sqrt{9})^2$
$= (4 + 3)^2= 49$
Now, the minimum value of $16 \sec^2 \Theta + 9 \csc^2 \Theta + 2$
$= 49 + 2= 51$
Hence, the answer is $51$.
Example 5: Find the maximum value of $8^{\sin \Theta} \times 16^{\cos \Theta}$.
Solution:
$8^{\sin \Theta} \times 16^{\cos \Theta} = 2^{3 \sin \Theta} \times 2^{4 \cos \Theta}$
$= 2^{3 \sin \Theta + 4 \cos \Theta}$
Maximum value of $a \sin \Theta + b \cos \Theta = \sqrt{a^2 + b^2}$
Maximum value of $3 \sin \Theta + 4 \cos \Theta = \sqrt{3^2 + 4^2}$
$= \sqrt{9 + 16}= 5$
Maximum value of $8^{\sin \Theta} \times 16^{\cos \Theta}$
$= 2^5= 32$
Hence, the answer is $32$.
List of Topics Related to the Trigonometric Equation using Minimum and Maximum value of Function
Below is the list of important topics linked with trigonometric equations based on the minimum and maximum values of functions, useful for Class 11 and competitive exam preparation.
NCERT Resources
Below are NCERT resources for Class 11 Chapter 3 – Trigonometric Functions, including detailed notes, NCERT solutions, and Exemplar solutions to help students strengthen concepts and practice effectively.
NCERT Class 11 Chapter 3 - Trigonometric Functions Notes
NCERT Class 11 solutions for Chapter 3 - Trigonometric Functions
NCERT Exemplar solutions for Class 11 Chapter 3 - Trigonometric Functions
Practice Questions on Trigonometric Equation using Minimum and Maximum Value of Function
Below are practice questions based on finding the minimum and maximum values of trigonometric functions, designed to improve problem-solving accuracy and conceptual clarity.
Trigonometric Equation Using Minimum And Maximum Value Of Function - Practice Question
We have provided below the links to practice questions on the related topics:
Frequently Asked Questions (FAQs)
The range of $\tan x$ is $[-\infty, \infty$ ]
The maximum and minimum values of the trignometric function cosecant is $\infty$ and $-\infty$ respectively.
Minimum value of the function stands for the lowest possible value of the function in the given range. The range of $\cos x$ is $[-1,1]$. So, the minimum value of $\cos x$ is -1 .
The maximum and minimum values of trigonometric functions depend upon the range of the trigonometric functions. The minimum value of the trigonometric function is the lowest value of the range and the maximum value is the highest value of the range.
The maximum value means the highest possible value in the given range. Since, the range of $\sin x$ is $[-1,1]$. So, The maximum value of $\sin X$ is 1 at $\mathrm{X}=\frac{\pi}{2}$