Signs of Trigonometric Functions

The trigonometric ratios of a given angle are the ratios of a right-angled triangle's sides with regard to any one of its acute angles. In real life, we use trigonometry in navigation and oceanography. It is also used in the creation of maps.

In this article, we will cover the concept of Sign of Trigonometric Functions. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Questions based on this topic have been asked frequently in JEE Mains.

What are Trigonometry ratios?

The trigonometric ratios of a given angle are the ratios of a right-angled triangle's sides with regard to any one of its acute angles.The six trigonometric ratios are sine (sin) , cosine (cos) , tangent(tan), cotangent(cot) , secant(sec) , cosecant(cosec) .

Sign of Trigonometric Functions

The sign of trigonometric ratios of an angle depends on the quadrant in which the terminal side of the angle lies. We always take $OP = r$ as positive. Thus, the sign of trigonometric functions depends on the sign of $x and y$.

Assume $r=1$, since this is a unit circle.
Let $P(a, b)$ be any point on the circle with angle $A O P=x$ radian i.e., length of $\operatorname{arc} A P=x$. Clearly $\cos x=a$ and $\sin x=b$,
In the right triangle $OMP$,

$
\begin{aligned}
& O M^2+M P^2=O P^2 \\
& x^2+y^2=1
\end{aligned}
$
Thus, for every point on the unit circle, we have $x^2+y^2=1$ or $\cos ^2 x+\sin ^2 x=1$.
Since one complete revolution subtends an angle of $2 \pi$ radian at the centre of the circle, $\angle A O B=\pi / 2 \angle A O C=\pi$ and $\angle A O D=3 \pi / 2$.
All angles which are integral multiples of $\pi / 2$ are quadrantile angles.
Therefore, for quadrantile angles, we have

$
\cos 0=1, \sin 0=0, \cos \pi / 2=0, \sin \pi / 2=1 . .
$
Now, if we take one complete revolution from the point $P$, we again come back to the same point $P$.
Thus, we also observe that if $x$ increases (or decreases) by an integral multiple of $2 \pi$, the values of sine and cosine functions do not change.

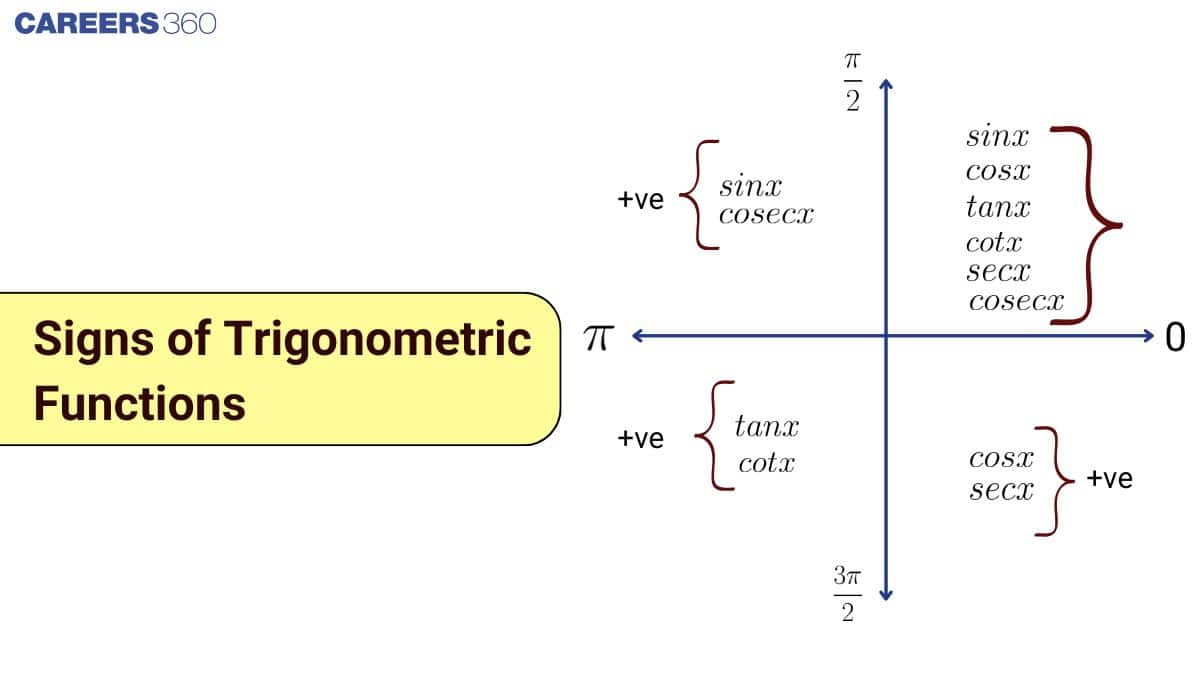
Variation in the Values of Trigonometric Functions in Different Quadrants

We observe that in the first quadrant, as $x$ increases from $0$ to $\pi / 2$, $\sin x$ increases from $0$ to $1$ and $\cos x$ decreases from $1$ to $0$ .
So, in the first quadrant, cosec $x$ decreases from infinity (when $x$ tends to zero) to $1$ , and $\sec x$ increases from 1 to infinity (when $x$ tends to $\pi / 2$ ). Also, tan $x$ increases from 0 to infinity (when $x$ tends to $\pi / 2$ ) and cot $x$ decreases from infinty (when $x$ tends to ) to $0$ . In the second quadrant, as $x$ increases from $\pi / 2$ to $\pi, \sin x$ decreases from $1$ to $0$ and $\cos x$ decreases from $0$ to $1$ . From these, we can find variations of other trigonometric functions in this quadrant.

An angle is said to be in a quadrant in which its terminal ray lies (here terminal ray is $OP$).
1. In the first quadrant $x$ and $y$ are positive $\operatorname{so} \sin \theta, \cos \theta, \tan \theta, \sec \theta, \csc \theta$, and $\cot \theta$ are all positive.
2. In the second quadrant, $x$ is negative and $y$ is positive, so only $\sin \theta$ and $\operatorname{cosec} \theta$ are positive.
3. In the third quadrant, $x$ is negative and $y$ is negative, so only $\tan \theta$ and $\cot \theta$ are positive.
4. In the fourth quadrant, $x$ is positive and $y$ is negative, so only $\cos \theta$ and $\sec \theta$ are positive.

To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase "After School to College". Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise.

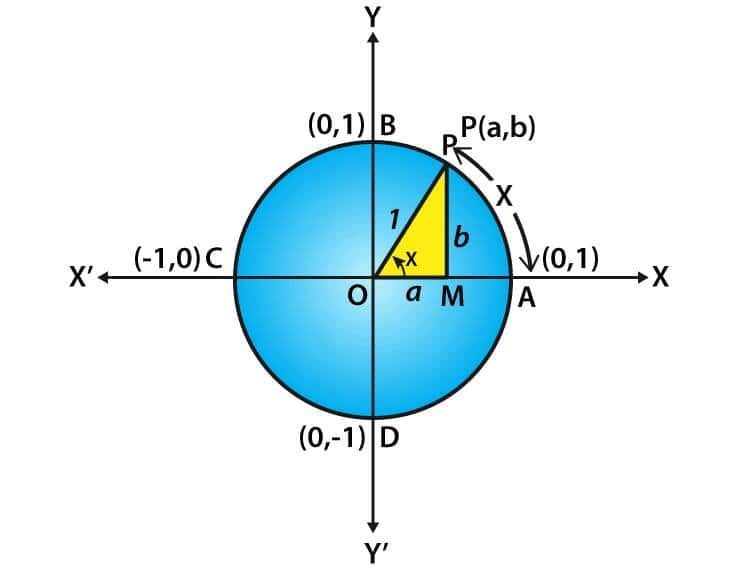
Depending on the signs of $x$ and $y$, the various trigonometric ratios will have different signs.

Domain of trigonometric functions

We observe that point $\mathrm{P}(\mathrm{a}, \mathrm{b})$ can be obtained by any amount of rotation of ray OP , clockwise or anticlockwise. Therefore, $\sin \mathrm{x}$ and $\cos \mathrm{x}$ functions are defined for all real values of x . The domain of these functions is $R$. Functions tan x and $\sec (x)$ are defined for all values $x$ except values of $x$ where $\cos x=0$. So, the domain of both the functions $\tan x$ and $\sec$ is
Domain is $\mathbb{R}-\left\{\frac{(2 \mathrm{n}+1) \pi}{2}, \mathrm{n} \in \mathbb{I}\right\}$
Functions $\cot \mathrm{x}$ and $\operatorname{cosec} \mathrm{x}$ are defined for all values x except values of x where $\sin \mathrm{x}=0$
So, the domain of both the functions $\cot x$ and $\operatorname{cosec} x$ is $R-\{n \pi, n \in I$ (Integers) $\}$.

Range of Trigonometric Functions

Since for every point $\mathrm{P}(\mathrm{a}, \mathrm{b})$ on the unit circle, $-1<\mathrm{a}<1$ and $-1<\mathrm{b}<1$ we have $-1<\cos \mathrm{x}<1$ and $-1<\sin \mathrm{x}<1$ for all x .
Thus, range of each of $\sin x$ and $\cos x$ is $[-1,1]$.

Summary

The signs of trigonometric functions sine, cosine, and tangent are determined by the quadrant in which the angle lies on the unit circle. These sign patterns hold true due to the periodic nature of trigonometric functions, where angles repeat every $2 \pi$ radians (or $360$ degrees). Understanding these sign conventions is crucial for correctly interpreting and solving trigonometric equations and inequalities across various contexts and aplications in mathematics and science.

Recommended Video

Solved Examples Based on Sign of Trigonometric Functions

Example 1: If $A B C D$ is a convex quadrilateral such that $4 \sec A+5=0$ then the quadratic equation whose roots are $\tan A$ and $\operatorname{cosec} A$ is:
Solution: Given that $4 \sec A+5=0$

$
\Rightarrow \sec A=-\frac{5}{4}
$
As the quadrilateral is convex So $\frac{\pi}{2}<A<\pi$ So, $\tan A=-\frac{3}{4}, \operatorname{cosec} A=\frac{5}{3}$

The quadratic equation with $\tan \mathbf{A}, \operatorname{cosec} \mathbf{A}$ as roots is

$
\left(x+\frac{3}{4}\right)\left(x-\frac{5}{3}\right)=0
$

or, $12 \times 2-11 x-15=0$
Hence, the quadratic equation whose roots are $\tan A$ and $\operatorname{cosec} A$ is $12 x 2-11 x-15=0$.

Example 2: Find the range of function $f(x)=1 /(2 \sin (X)-3)$
Solution:

$
\begin{aligned}
& \mathrm{f}(x)=\frac{1}{2 \sin x-3} \\
& -1 \leq \sin x \leq 1 \\
& \Rightarrow-2 \leq 2 \sin x \leq 2 \\
& \Rightarrow-2-3 \leq 2 \sin x-3 \leq 2-3 \\
& \Rightarrow \frac{1)}{f(x)} \leq-1 \\
& \Rightarrow f(x) \epsilon[-1,0) \\
& \Rightarrow \frac{1)}{f(x)} \geq-5 \\
& \Rightarrow f(x) \epsilon\left(-\infty, \frac{-1}{5}\right] U(0, \infty) b y \text { both inequalities } f(x) \epsilon\left[-1,-\frac{1}{5}\right]
\end{aligned}
$

Example 3: If $\frac{3 \pi}{4}<\alpha<\pi$, then $\sqrt{\csc ^2 \alpha+2 \cot \alpha}$ is equal to?

$
\begin{aligned}
& \text { Solution } \\
& \sqrt{\csc ^2 \alpha+2 \cot \alpha} \\
& =\sqrt{1+\cot ^2 \alpha+2 \cot \alpha} \\
& =\sqrt{(1+\cot \alpha)^2} \\
& =|1+\cot \alpha|
\end{aligned}
$

Hence, the answer is $-1-\cot \alpha$
Example 4: If $x$ lies in the third quadrant, then the expression $\sqrt{3-\sqrt{\frac{1}{1+\cot ^2 x}}}$ equals
Solution

$
\begin{aligned}
& \sqrt{3-\sqrt{\frac{1}{1+\cot ^2 x}}} \\
& =\sqrt{3-\sqrt{\frac{1}{\csc ^2 x}}} \\
& =\sqrt{3-|\sin x|}
\end{aligned}
$
Now as $x$ lies in third quadrant, so $\sin (x)<0$, and thus $|\sin (x)|=-\sin (x)$
So the given expression equals

$
\sqrt{3+\sin (x)}
$
Hence, the answer is $\sqrt{3+\sin (x)}$

Example 5: The value of the trigonometric function $\operatorname{cosec}\left(-1350^{\circ}\right)$ is.
Solution: The values of cosec x repeat after an interval of $2 \pi$ or $360^{\circ}$.
Now,
$
\begin{aligned}
& \operatorname{cosec}\left(-1350^{\circ}\right)=\operatorname{cosec}\left(-1350^{\circ}+4 \times 360^{\circ}\right) \\
& \operatorname{cosec}\left(-1350^{\circ}\right)=\operatorname{cosec}\left(-1350^{\circ}+1440^{\circ}\right) \\
& \operatorname{cosec}\left(-1350^{\circ}\right)=\operatorname{cosec}\left(90^{\circ}\right) \\
& \operatorname{cosec}\left(-1350^{\circ}\right)=1
\end{aligned}
$