Roots are real and repeated.
Location of Roots: Quadratic Equation, Theorem, Formula, Questions
Understanding the location of roots of quadratic equations is a vital concept in algebra that plays a significant role in solving mathematical problems across physics, engineering, and economics. In mathematics, this topic helps identify whether the roots are positive, negative, real, or lie on opposite sides of the origin. For students preparing for competitive exams or looking to strengthen their algebra basics, mastering the location of roots in quadratic equations is essential. In this article, we explain the concept with clear explanations, examples, and key conditions to help you grasp it easily.
This Story also Contains
- Introduction to Location of Roots
- Standard Form of a Quadratic Equation
- Different Cases of Roots of a Quadratic Equation
- Sum and Product of Roots of a Quadratic Equation
- Graphical Interpretation of Location of Roots
- Important Formulae and Concepts for Quadratic Equations
- List of Topics related to the Location of Roots
- NCERT Useful Resources
- Practice Questions on the location of roots
Introduction to Location of Roots
The location of roots helps determine where the solutions (roots) of a quadratic equation lie on the number line—whether they are positive, negative, real, complex, or on opposite sides of a point (like the origin or a specific number). Instead of finding the exact values of the roots, the goal is to infer their signs and relative positions using logical conditions and basic algebraic tools.
What is the Location of Roots?
Given a quadratic equation
$ax^2 + bx + c = 0$
Let the roots be $x_1$ and $x_2$.
The location of roots describes whether:
Both roots are positive
Both roots are negative
Roots lie on opposite sides of zero (or any given number)
Roots are real and distinct, real and equal, or complex
Key Formulas to Analyze Root Location
Discriminant:
$D = b^2 - 4ac$
Sum of roots:
$x_1 + x_2 = \dfrac{-b}{a}$
Product of roots:
$x_1 \cdot x_2 = \dfrac{c}{a}$
Basic Conditions for Location and Nature of Roots
Roots are real and distinct if $D > 0$
Roots are real and equal if $D = 0$
Roots are complex (non-real) if $D < 0$
Both roots are positive if $x_1 + x_2 > 0$ and $x_1 \cdot x_2 > 0$
Both roots are negative if $x_1 + x_2 < 0$ and $x_1 \cdot x_2 > 0$
Roots lie on opposite sides of zero if $x_1 \cdot x_2 < 0$
Standard Form of a Quadratic Equation
Quadratic equations are algebraic equations of degree 2, and understanding their form is essential before studying the location of roots. The standard form of a quadratic equation is
$ax^2 + bx + c = 0$,
where $a, b,$ and $c$ are real constants and $a \ne 0$.
To find the location of roots of a function, several well-known methods are used, such as the sign change method, graphical method to locate roots, Intermediate Value Theorem, Rolle’s Theorem, and Descartes’ Rule of Signs. These techniques help estimate where the roots lie on the number line without always solving the equation exactly.
Understanding how to find the approximate location of roots of a polynomial makes solving quadratic and higher-degree equations easier, more visual, and more intuitive—an essential skill in algebra and graph-based problem solving.
Meaning of Roots or Zeros of a Quadratic Equation
The roots (or zeros) of a quadratic equation are the values of $x$ that satisfy
$ax^2 + bx + c = 0$.
These roots represent the x-intercepts of the parabola defined by
$f(x) = ax^2 + bx + c$.
Understanding the location of roots is essential when analysing the graph of a quadratic function, as it tells us where the graph crosses or touches the x-axis.
The roots of a quadratic equation can be found using the quadratic formula:
$x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
To further study how to find the location of roots of a polynomial, methods such as the graphical method to locate roots, the sign change method for roots, and the Intermediate Value Theorem are widely used. These techniques help in finding the location of roots of an equation, estimating their values, and understanding whether the roots are real, repeated, or complex, without always solving the equation exactly.
Real vs Complex Roots
The discriminant $D=b^2−4ac$ determines the nature of the roots:
- If D>0, roots are real and distinct
- If D=0, roots are real and equal
- If D<0, roots are complex conjugates
This classification is crucial for analyzing where and how the roots appear on the number line or complex plane.
Conditions for Location of Roots in Quadratic Equations
To determine the location of roots of a quadratic equation, several algebraic tests based on the coefficients and discriminant are used. These methods help in understanding how to find the location of roots of a polynomial and whether the roots lie on the positive or negative side of the number line. Techniques such as the sign change method for locating roots, the Intermediate Value Theorem, and concepts related to Rolle’s Theorem and root location are commonly applied. Together, these approaches make it easier to identify the position, nature, and behavior of roots without solving the equation completely.
Discriminant and Nature of Roots $D=b^2−4ac$
Use it to decide:
- D>0: Two real and distinct roots
- D=0: Real and equal roots
- D<0: No real roots (complex)
Real roots are necessary to discuss their location on the number line.
Sign of Roots Based on Coefficients
Using formulas:
Sum of roots:
$x_1 + x_2 = \dfrac{-b}{a}$
Product of roots:
$x_1 \cdot x_2 = \dfrac{c}{a}$
Conditions:
If $x_1 + x_2 > 0$, both roots are positive.
If $x_1 + x_2 < 0$, both roots are negative.
If $x_1 \cdot x_2 < 0$, the roots lie on opposite sides of zero.
Location of Roots on the Number Line
To determine where the roots lie:
- Check sign of f(x) at a point (like f(0)=c)
- Analyze the sign of the product $x_1⋅x_2$
- Graphical approach: roots are x-intercepts of the parabola
Quick checks:
- $f(0) = c > 0$ ⇒ roots lie on opposite sides of $0$
- If $x_1 + x_2 > 0$ and $x_1 \cdot x_2 > 0$, the roots lie on the positive side.
- Whether the roots are both positive or both negative depends on the sign consistency of the function.
Importance in Algebra and Real-World Applications
The concept of location of roots is widely used in:
- Algebra: For solving inequalities and analyzing signs of expressions without solving the equation fully.
- Graphing: Understanding whether the parabola intersects the x-axis and where.
- Inequalities: For checking when $ax^2+bx+c>0$ or $<0$ based on root positions.
- Physics and Engineering: To ensure solutions (e.g., time, speed) are positive and physically meaningful.
- Economics: For identifying profit/loss break-even points based on quadratic cost/revenue functions.
Different Cases of Roots of a Quadratic Equation
The nature and location of roots of a quadratic equation $ax^2+bx+c=0$ largely depend on the discriminant $D=b^2−4ac$. Understanding this helps in finding location of roots of equation more effectively.
Different cases—real and distinct, real and equal, or complex roots—affect how to locate roots of a function both algebraically and visually. Methods like the graphical method to locate roots, Descartes' Rule of Signs, and the intermediate value theorem for roots can assist in analysing these scenarios.
Case 1: D>0 – Real and Distinct Roots
Roots are real and unequal.
If $\dfrac{c}{a} > 0$ and $\dfrac{-b}{a} > 0$, both roots are positive.
If $\dfrac{c}{a} > 0$ and $\dfrac{-b}{a} < 0$, both roots are negative.
If $\dfrac{c}{a} < 0$, the roots lie on opposite sides of the origin.
Case 2: D=0 – Real and Equal Roots
The single root is given by $x = \dfrac{-b}{2a}$
The root is positive if $\dfrac{-b}{2a} > 0$ and negative if $\dfrac{-b}{2a} < 0$
Case 3: D<0 – Imaginary Roots
- Roots are non-real (complex conjugate pair).
- No real root exists ⇒ no location on the number line.
Case 4: D is a Perfect Square
- Roots are real and rational
- Examples: D=4, 9, 16, etc.
- Occurs often in factorable quadratic equations
Case 5: D is Not a Perfect Square
- Roots are real and irrational.
- Cannot be simplified to a rational number.
- Roots still follow the same sign rules using sum and product.
Sum and Product of Roots of a Quadratic Equation
Let $\alpha$ and $\beta$ be the roots of the quadratic equation
$ax^2 + bx + c = 0$
Sum of Roots Formula
$\alpha + \beta = \dfrac{-b + \sqrt{D}}{2a} + \dfrac{-b - \sqrt{D}}{2a}$
$= \left(\dfrac{-b}{2a} + \dfrac{\sqrt{D}}{2a}\right) + \left(\dfrac{-b}{2a} - \dfrac{\sqrt{D}}{2a}\right)$
$= \dfrac{-2b}{2a}$
$= \dfrac{-b}{a}$
So, the sum of roots is
$\alpha + \beta = \dfrac{-b}{a}$
Product of Roots Formula
$\alpha \cdot \beta = \left(\dfrac{-b + \sqrt{D}}{2a}\right)\left(\dfrac{-b - \sqrt{D}}{2a}\right)$
$= \dfrac{(-b)^2 - (\sqrt{D})^2}{(2a)^2}$
$= \dfrac{b^2 - D}{4a^2}$
$= \dfrac{b^2 - (b^2 - 4ac)}{4a^2}$
$= \dfrac{4ac}{4a^2}$
$= \dfrac{c}{a}$
So, the product of roots is
$\alpha \cdot \beta = \dfrac{c}{a}$
Forming a Quadratic Equation from Roots
Given $\alpha + \beta$ and $\alpha \cdot \beta$, the quadratic equation is
$x^2 - (\alpha + \beta)x + (\alpha \cdot \beta) = 0$
Substituting the given values,
$x^2 - \dfrac{b}{a}x + \dfrac{c}{a} = 0$
Multiplying the entire equation by $a$,
$ax^2 - bx + c = 0$
This is the original quadratic equation reconstructed using the sum and product of roots.
Graphical Interpretation of Location of Roots
Now, the question is: how to find the location of roots?
The graphical method to locate roots provides a visual way to understand the location of roots in a quadratic equation. For any equation of the form
$f(x) = ax^2 + bx + c$,
the graph is a parabola, and its x-intercepts represent the real roots of the equation.
Whether the parabola cuts the x-axis at two points, touches it at one point, or does not intersect it at all depends on the discriminant. This method is especially useful for finding the location of roots of a quadratic equation and for determining whether the roots are positive, negative, real, or complex.
Let
$f(x) = ax^2 + bx + c$, where $a, b,$ and $c$ are real numbers and $a \ne 0$.
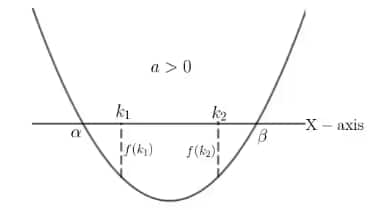
Let $x_1$ and $x_2$ be the roots of the equation, and let $k$ be a real number.
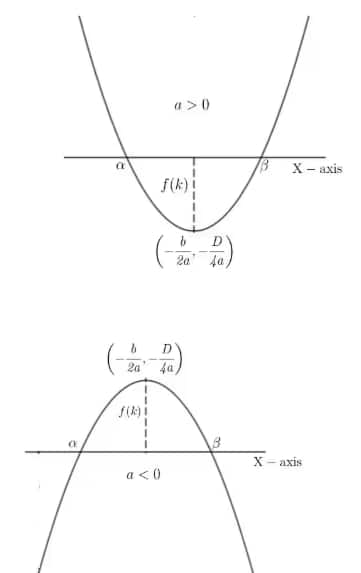
1. If both roots of f(x) are less than k then
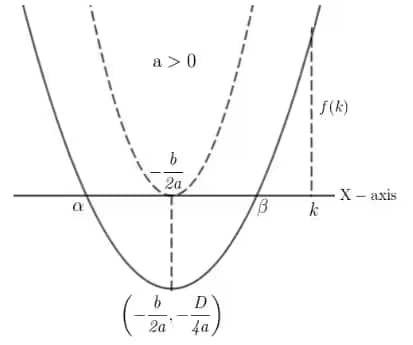
i) $D \ge 0$ (as the real roots may be distinct or equal)
ii) $a f(k) > 0$ (in both cases $a f(k)$ is positive; if $a < 0$, then $f(k) < 0$, and the product of two negative values is positive)
iii) $k > \dfrac{-b}{2a}$ since $\dfrac{-b}{2a}$ lies between $x_1$ and $x_2$, and $x_1, x_2$ are less than $k$, so $\dfrac{-b}{2a}$ is less than $k$
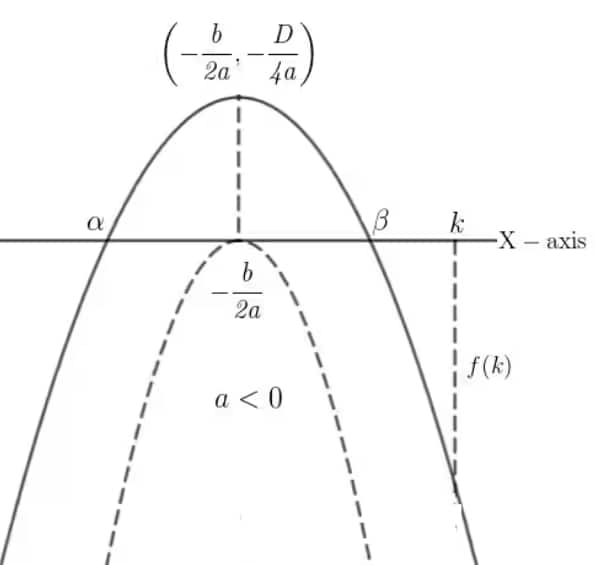
2. If both roots of f(x) are greater than k
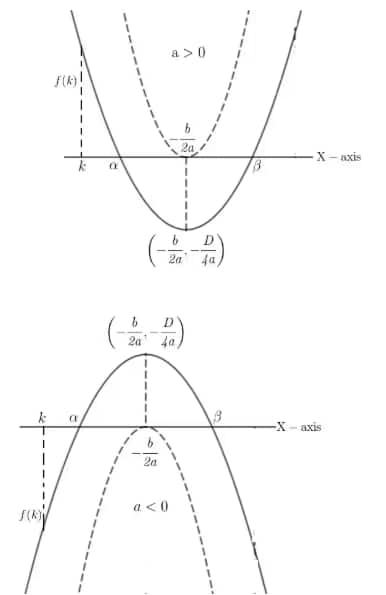
i) $D \ge 0$ (as the real roots may be distinct or equal)
ii) $a f(k) > 0$ (in both cases $a f(k)$ is positive; if $a < 0$, then $f(k) < 0$, and the product of two negative values is positive)
iii) $k < \dfrac{-b}{2a}$ since $\dfrac{-b}{2a}$ lies between $x_1$ and $x_2$, and $x_1, x_2$ are greater than $k$, so $\dfrac{-b}{2a}$ is also greater than $k$
Condition for number $k$
Let
$f(x) = ax^2 + bx + c$, where $a, b, c$ are real numbers and $a \ne 0$.
Let $x_1$ and $x_2$ be the real roots of the function, and let $k$ be any real number.
3. If k lies between the root $x_1$ and $x_2$
$a f(k) < 0$
As if $a < 0$, then $f(k) > 0$. So, multiplying one negative and one positive value gives a negative result.
Condition for numbers $k_1$ and $k_2$
Let
$f(x) = ax^2 + bx + c$, where $a, b, c$ are real numbers and $a \ne 0$.
Let $x_1$ and $x_2$ be the real roots of the function, and let $k_1, k_2$ be any two real numbers.
4. If exactly one root of f(x) lies in between the number $k_1,k_2$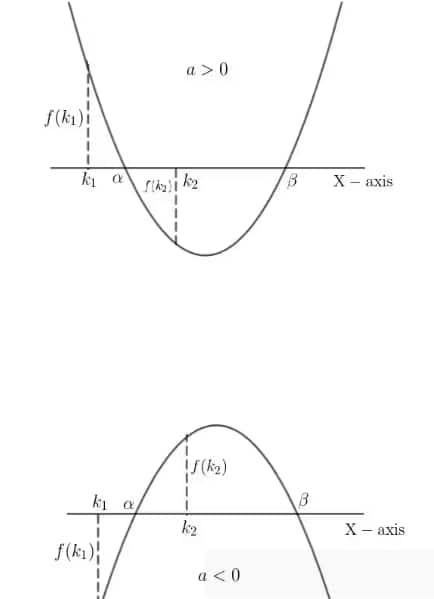
$f(k_1) f(k_2) < 0$, as for one value of $k$ we get a positive value of $f(x)$, and for the other value of $k$ we get a negative value of $f(x)$ (here $x_1 < x_2$).
Condition on numbers $k_1, k_2$
Let
$f(x) = ax^2 + bx + c$, where $a, b, c$ are real numbers and $a \ne 0$.
Let $x_1$ and $x_2$ be the roots of the function, and let $k_1, k_2$ be any two real numbers.
5. If both roots lie between $k_1,k_2$
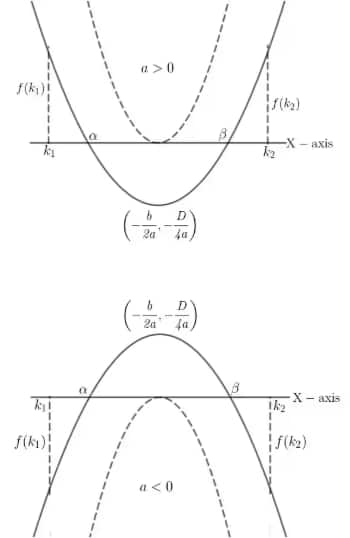
i) $D \ge 0$ (as the real roots may be distinct or equal)
ii) $k_1 < \dfrac{-b}{2a} < k_2$, where $a \le 3$ and $k_1 < k_2$
6. If $k_1,k_2$ lies between the roots
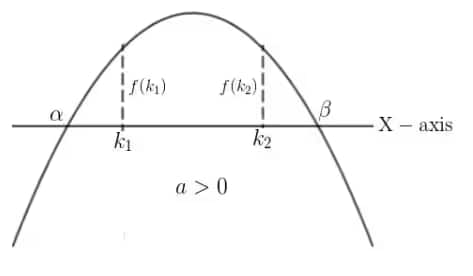 $a f(k_1) < 0$ and $a f(k_2) < 0$
$a f(k_1) < 0$ and $a f(k_2) < 0$
Important Formulae and Concepts for Quadratic Equations
The following table highlights the important formulae and key concepts of quadratic equations, helping you quickly analyze the nature and location of roots without lengthy calculations.
| Concept | Formula/Condition |
|---|---|
| Standard quadratic equation | $ax^2 + bx + c = 0$ |
| Discriminant | $D = b^2 - 4ac$ |
| Sum of roots | $x_1 + x_2 = \dfrac{-b}{a}$ |
| Product of roots | $x_1 \cdot x_2 = \dfrac{c}{a}$ |
| Roots are real and distinct | $D > 0$ |
| Roots are real and equal | $D = 0$ |
| Roots are complex (non-real) | $D < 0$ |
| Both roots positive | $x_1 + x_2 > 0$ and $x_1 \cdot x_2 > 0$ |
| Both roots negative | $x_1 + x_2 < 0$ and $x_1 \cdot x_2 > 0$ |
| Roots on opposite sides of zero | $x_1 \cdot x_2 < 0$ |
| Repeated root (equal roots) | $x = \dfrac{-b}{2a}$ |
| Axis of symmetry (helps in root location) | $x = \dfrac{-b}{2a}$ |
Solved Examples Based on Location of Roots
Example 1: Number of +ve integer values of 'a' for which $x^2+x+a=0$ has roots of opposite sign is.......
Solution:
Roots are of opposite sign.
$ \dfrac{c}{a} < 0 $ and $ D = b^2 - 4ac > 0 $
$D > 0$
$\dfrac{c}{a} < 0 \Rightarrow 1 - 4a > 0$
$a - 1 < 0$
$\Rightarrow a < 1$
$\Rightarrow a < 0$
Hence, the number of positive integer values of $a$ is $0$.
a) −2<m<0
b) m>3
c) −1<m<3
d) 1<m<4
Solution:
For both roots to exist,
$D > 0$
$D = b^2 - 4ac$
$\Rightarrow D = 4m^2 - 4(m^2 - 1)$
$\Rightarrow D = 4$
Here, $D > 0$
Now,
$f(-2) > 0$ and $f(4) > 0$
$\Rightarrow 4 + 4m + m^2 - 1 > 0$ and $16 - 8m + m^2 - 1 > 0$
$\Rightarrow m^2 + 4m + 3 > 0$ and $m^2 - 8m + 15 > 0$
$\Rightarrow (m+3)(m+1) > 0$ and $(m-5)(m-3) > 0$
$\Rightarrow m \in (-\infty,-3) \cup (-1,\infty)$
and
$m \in (-\infty,3) \cup (5,\infty)$
Taking the intersection of the above intervals,
$m \in (-1,3)$
Therefore, $m$ should belong to $(-1,3)$ for the roots to lie between $-2$ and $4$.
Example 3: What is the value of m so that both roots of the equation $x^2+mx+1$ are less than unity?
Solution:
Since the roots are less than unity, it implies that
$a f(1) > 0$, where $a = 1$ and $f(1) = m + 2$
So,
$m + 2 > 0 \Rightarrow m > -2$ ...(i)
For two distinct real roots to exist, the discriminant must be positive:
$D > 0 \Rightarrow m^2 - 4 > 0$
So,
$m > 2$ or $m < -2$ ...(ii)
Now, combining (i) and (ii):
From (i): $m > -2$
From (ii): $m > 2$ or $m < -2$
The common values satisfying both conditions are:
$m > 2$
Hence, the final solution is:
$m > 2$
Solution:
If one root is less than $2$ and $f(2) < 0$
$D > 0$
$(m-3)^2 - 4m > 0$
$(m-1)(m-9) > 0$
$m \in (-\infty, 1) \cup (9, \infty)$
Now,
$f(2) < 0$
$4 - 2(m-3) + m < 0$
$10 - m < 0$
$m > 10$
On combining both conditions,
$m \in (10, \infty)$
Solution:
If exactly one root of the equation
$x^2 + 2ax + a^2 - 1 = 0$
lies between $4$ and $6$, then
$f(4)\cdot f(6) < 0$
$(16 + 8a + a^2 - 1)(36 + 12a + a^2 - 1) < 0$
$(a^2 + 8a + 15)(a^2 + 12a + 35) < 0$
$(a+5)(a+3)(a+7)(a+5) < 0$
$(a+3)(a+7)(a+5)^2 < 0$
$(a+3)(a+7) < 0$
$a \in (-7,-3)$
List of Topics related to the Location of Roots
Here is a list of key topics related to the location of roots in quadratic equations and polynomials, including concepts like remainder theorem, rational and irrational inequalities, along with exponential and logarithmic equations in quadratic form.
NCERT Useful Resources
Explore essential NCERT study materials for Complex Numbers and Quadratic Equations, including detailed solutions, concise revision notes, and curated exemplar problems. These resources are tailored to help you strengthen your conceptual understanding and prepare effectively for board and competitive exams.
Practice Questions on the location of roots
To help you strengthen your understanding of the topic, we’ve included a few practice questions on location of roots of quadratic equations. These will test your grasp of root positions, signs, and related conditions using standard formulas.
To practice location of roots-based questions, click here.
You can practice the next topics of Complex Numbers and Quadratic Equations below: