Remainder Theorem - Polynomials, Statement, Proof and Examples

Relationship Between Coefficients and Roots of a Polynomial

One of the most important results in polynomial algebra is the relationship between the coefficients of a polynomial and its roots. These relationships help us find the sum and product of roots without actually solving the polynomial equation. They are widely used in algebra, higher mathematics, competitive examinations, and polynomial transformations.

Consider the polynomial equation:

$a_0x^n+a_1x^{n-1}+a_2x^{n-2}+\cdots+a_n=0$

where:

• $a_0 \neq 0$
• $\alpha_1,\alpha_2,\alpha_3,\ldots,\alpha_n$ are the roots of the polynomial.

Sum of All Roots

The sum of all roots is given by:

$\alpha_1+\alpha_2+\cdots+\alpha_n=-\frac{a_1}{a_0}$

or

$\sum \alpha_i=-\frac{a_1}{a_0}$

Sum of Products of Roots Taken Two at a Time

The sum of products of roots taken two at a time is:

$\alpha_1\alpha_2+\alpha_1\alpha_3+\cdots+\alpha_{n-1}\alpha_n=\frac{a_2}{a_0}$

or

$\sum \alpha_i\alpha_j=\frac{a_2}{a_0}$

Sum of Products of Roots Taken Three at a Time

The sum of products of roots taken three at a time is:

$\sum \alpha_i\alpha_j\alpha_k=-\frac{a_3}{a_0}$

Product of All Roots

The product of all roots is:

$\alpha_1\alpha_2\cdots\alpha_n=(-1)^n\frac{a_n}{a_0}$

Example

Consider the cubic polynomial:

$ax^3+bx^2+cx+d=0$

Let the roots be:

$\alpha,\beta,\gamma$

Then:

$\alpha+\beta+\gamma=-\frac{b}{a}$

$\alpha\beta+\beta\gamma+\gamma\alpha=\frac{c}{a}$

$\alpha\beta\gamma=-\frac{d}{a}$

These formulas are frequently used in polynomial equations and algebraic transformations.

Transformation of Roots

Root transformation refers to finding a new polynomial whose roots are related to the roots of the original polynomial through a specific transformation.

The procedure is similar to the transformation of roots used in quadratic equations.

Common transformations include:

• Increasing each root by a constant.
• Decreasing each root by a constant.
• Taking reciprocals of roots.
• Multiplying roots by a constant.
• Applying algebraic expressions to roots.

Transformation of roots is widely used in higher algebra and polynomial theory.

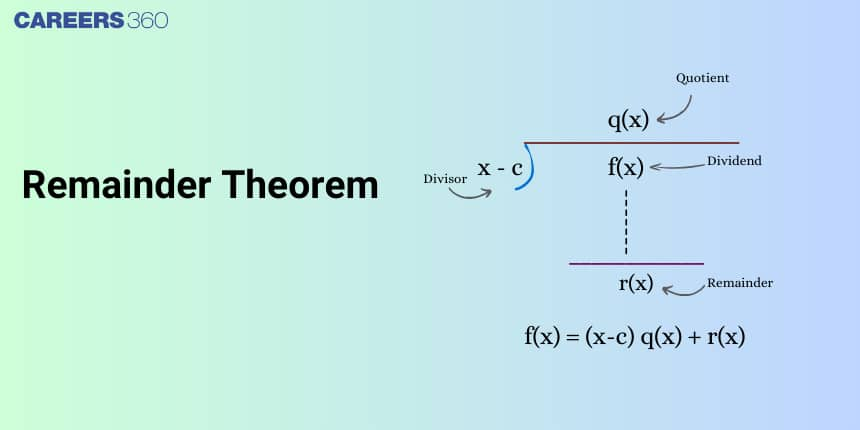
Remainder Theorem

The Remainder Theorem provides a simple way to determine the remainder when a polynomial is divided by a linear polynomial.

Statement of the Remainder Theorem

If a polynomial $f(x)$ is divided by a linear polynomial $(x-k)$, then the remainder obtained is equal to $f(k)$.

Mathematically:

Remainder $=f(k)$

Polynomial Division Form

For polynomial division:

$f(x)=d(x)\cdot q(x)+r(x)$

where:

• $f(x)$ = dividend
• $d(x)$ = divisor
• $q(x)$ = quotient
• $r(x)$ = remainder

The degree of the remainder is always less than the degree of the divisor.

If the divisor is a linear polynomial $(x-k)$, then the remainder must be a constant.

Therefore:

$f(x)=(x-k)q(x)+R$

where $R$ is a constant remainder.

Proof of the Remainder Theorem

Substitute:

$x=k$

in

$f(x)=(x-k)q(x)+R$

Then:

$f(k)=(k-k)q(k)+R$

$f(k)=0+R$

$f(k)=R$

Therefore,

Remainder $=f(k)$

Hence proved.

Example

Find the remainder when:

$f(x)=2x^3-3x-4$

is divided by:

$(x-3)$

Here:

$k=3$

Using the theorem:

$f(3)=2(3)^3-3(3)-4$

$=54-9-4$

$=41$

Therefore, the remainder is:

$\boxed{41}$

Steps to Divide a Polynomial by a Non-Zero Polynomial

Polynomial division follows a systematic procedure similar to numerical long division.

Step 1

Arrange both the dividend and divisor in descending order of powers.

Step 2

Divide the first term of the dividend by the first term of the divisor.

Step 3

Write the result as the next term of the quotient.

Step 4

Multiply the divisor by this quotient term.

Step 5

Subtract the resulting expression from the dividend.

Step 6

Treat the new remainder as the next dividend.

Step 7

Repeat the process until the degree of the remainder becomes less than the degree of the divisor.

The final expression obtained is the remainder.

Euler's Remainder Theorem

Euler's Theorem is one of the most important results in number theory.

Statement of Euler's Theorem

If $X$ and $n$ are coprime positive integers, then:

$X^{\varphi(n)}\equiv1\pmod n$

where $\varphi(n)$ is Euler's Totient Function.

Euler's Totient Function

If

$n=a^pb^qc^r$

where:

• $a,b,c$ are distinct prime numbers
• $p,q,r$ are positive integers

then:

$\varphi(n)=n\left(1-\frac{1}{a}\right)\left(1-\frac{1}{b}\right)\left(1-\frac{1}{c}\right)$

Euler's theorem is widely used in modular arithmetic, cryptography, and number theory.

Factor Theorem

The Factor Theorem is a direct extension of the Remainder Theorem.

Statement of the Factor Theorem

If:

$f(k)=0$

then:

$(x-k)$ is a factor of $f(x)$

In other words, if the remainder becomes zero, the divisor becomes a factor of the polynomial.

Why Does It Work?

From the Remainder Theorem:

Remainder $=f(k)$

If:

$f(k)=0$

then:

Remainder $=0$

Therefore:

$(x-k)$ divides $f(x)$ exactly.

Hence:

$(x-k)$ is a factor of $f(x)$.

Example

Consider:

$f(x)=x^3+3x-4$

Check:

$f(1)=1+3-4$

$=0$

Since:

$f(1)=0$

Therefore:

$(x-1)$ is a factor of $f(x)$.

Difference Between the Remainder Theorem and Factor Theorem

Both theorems are closely related, but their applications are different.

Example Comparison

Consider:

$p(x)=6x^4-x^3+2x^2-7x+2$

When divided by:

$(2x+3)$

Suppose the calculated remainder is:

$\frac{203}{4}$

Using the Remainder Theorem, we conclude that the remainder is non-zero.

Therefore, by the Factor Theorem:

$(2x+3)$ is not a factor of the polynomial.

This demonstrates how the Remainder Theorem helps calculate the remainder, while the Factor Theorem uses that remainder to determine whether a polynomial factor exists.

Best Books for Remainder Theorem

A strong foundation in polynomial algebra is necessary for understanding the Remainder Theorem, Factor Theorem, and polynomial division techniques.

Shortcut Tips and Tricks for Remainder Theorem

The Remainder Theorem can save significant time by avoiding lengthy polynomial division.

Important Formula Table

This table provides the key formulas related to the Remainder Theorem and polynomial division.

Solved Examples based on Remainder Theorem

Question 1: If $2+3i$ is one of the roots of the equation $2x^3-9x^2+kx-13=0$, where $k\in\mathbb{R}$, then the real root of this equation is:

1. Does not exist
2. $\frac{1}{2}$
3. $-\frac{1}{2}$
4. $1$

Solution:

For the cubic equation

$ax^3+bx^2+cx+d=0$

we know that:

$\alpha+\beta+\gamma=-\frac{b}{a}$

and

$\alpha\beta\gamma=-\frac{d}{a}$

Since complex roots occur in conjugate pairs,

$\alpha=2+3i$

$\beta=2-3i$

Let the third root be $\gamma$.

Using the product of roots:

$\alpha\beta\gamma=\frac{13}{2}$

$(2+3i)(2-3i)\gamma=\frac{13}{2}$

$(4+9)\gamma=\frac{13}{2}$

$13\gamma=\frac{13}{2}$

$\gamma=\frac{1}{2}$

Hence, the real root is $\frac{1}{2}$.

Answer: Option (2)

Question 2: The sum of the real roots of the equation $\begin{vmatrix}
x & -6 & -1\\
2 & -3x & x-3\\
-3 & 2x & x+2
\end{vmatrix}=0$ is equal to:

1. 6
2. 0
3. 1
4. -4

Solution:

Expanding the determinant and simplifying gives:

$x^3-7x+6=0$

Factorizing:

$x^3-7x+6=(x-1)(x-2)(x+3)$

Therefore, the roots are:

$1, 2, -3$

Sum of roots:

$1+2-3=0$

Hence, the sum of the real roots is $0$.

Answer: Option (2)

Question 3: Let $\alpha,\beta$ be two roots of $x^3+px^2+qx+r=0$ and satisfy $\alpha\beta=-1$. If $r\neq0$, then $|r^2+pr+q|$ equals:

1. 0
2. 1
3. 2
4. 3

Solution:

For the cubic equation

$x^3+px^2+qx+r=0$

let the third root be $\gamma$.

Using the product of roots:

$\alpha\beta\gamma=-r$

Since

$\alpha\beta=-1$

therefore

$(-1)\gamma=-r$

$\gamma=r$

Since $\gamma$ is a root, it satisfies the equation:

$r^3+pr^2+qr+r=0$

$r(r^2+pr+q+1)=0$

Given $r\neq0$,

$r^2+pr+q+1=0$

$r^2+pr+q=-1$

Therefore,

$|r^2+pr+q|=|-1|=1$

Answer: Option (2)

Question 4: If $\alpha,\beta,\gamma$ are the roots of $x^3-x^2-1=0$, then $\frac{\alpha+1}{\alpha}+\frac{\beta+1}{\beta}+\frac{\gamma+1}{\gamma}$ is equal to:

1. 2
2. 3
3. 4
4. 5

Solution:

For

$x^3-x^2-1=0$

we have:

$\alpha+\beta+\gamma=1$

$\alpha\beta+\beta\gamma+\gamma\alpha=0$

$\alpha\beta\gamma=1$

Now,

$\frac{\alpha+1}{\alpha}+\frac{\beta+1}{\beta}+\frac{\gamma+1}{\gamma}$

$=\left(1+\frac{1}{\alpha}\right)+\left(1+\frac{1}{\beta}\right)+\left(1+\frac{1}{\gamma}\right)$

$=3+\left(\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}\right)$

$=3+\frac{\alpha\beta+\beta\gamma+\gamma\alpha}{\alpha\beta\gamma}$

$=3+\frac{0}{1}$

$=3$

Hence, the required value is $3$.

Answer: Option (2)

Question 5: If $\alpha,\beta,\gamma$ are the roots of $x(1+x^2)+x^2(6+x)+2=0$ then $\alpha^{-1}+\beta^{-1}+\gamma^{-1}$ equals:

1. $-1$
2. $-\frac{1}{2}$
3. $0$
4. $\frac{1}{2}$

Solution:

The equation becomes:

$2x^3+6x^2+x+2=0$

For a cubic equation

$ax^3+bx^2+cx+d=0$

we have:

$\alpha\beta+\beta\gamma+\gamma\alpha=\frac{c}{a}$

and

$\alpha\beta\gamma=-\frac{d}{a}$

Therefore,

$\alpha\beta+\beta\gamma+\gamma\alpha=\frac{1}{2}$

$\alpha\beta\gamma=-1$

Now,

$\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}$

$=\frac{\alpha\beta+\beta\gamma+\gamma\alpha}{\alpha\beta\gamma}$

$=\frac{\frac{1}{2}}{-1}$

$=-\frac{1}{2}$

Hence, the required value is $-\frac{1}{2}$.

Answer: Option (2)