Nature of Roots of Quadratic Equations: Formulas and Examples

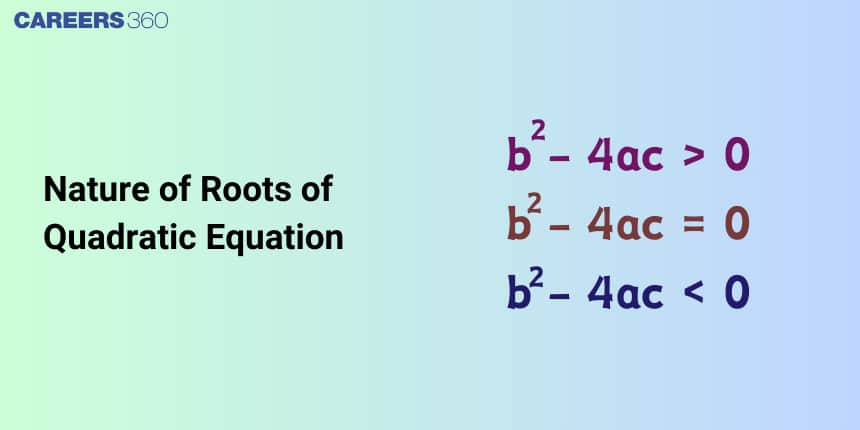
Nature of Roots of Quadratic Equations

Quadratic equations are polynomial equations of degree two, and their roots or solutions can be real, equal, unequal, or complex. Using the discriminant and the quadratic formula, we can quickly determine the type of roots without fully solving the equation. We will explore the types of roots of quadratic equations, how to find them, their graphical representation, special cases, and important formulas involving roots.

What Are the Roots of a Quadratic Equation?

In a quadratic equation, the term “roots” refers to the values of the variable, usually denoted as $x$, that satisfy the equation and make it true. The standard form of a quadratic equation is: $ax^2 + bx + c = 0$

Here, the roots are the values of $x$ which, when substituted, make the equation equal to zero. Depending on the discriminant, a quadratic equation can have zero, one, or two real roots.

Let the quadratic equation be:

$ax^2 + bx + c = 0, \quad a,b,c \in \mathbb{R}$

The discriminant of this equation is:

$D = b^2 - 4ac$

The roots of the quadratic equation are then given by the quadratic formula:

$x_1 = \frac{-b + \sqrt{D}}{2a}, \quad x_2 = \frac{-b - \sqrt{D}}{2a}$

Types of Roots of Quadratic Equations

In this section, we explore the different types of roots of quadratic equations, real and distinct, real and equal, or complex, using the discriminant to understand their nature and behavior in equations and graphs.

Real and Distinct Roots

• Occur when $D > 0$

• The quadratic curve intersects the $x$-axis at two distinct points

• Roots can be rational or irrational, depending on whether $D$ is a perfect square

Example: For $x^2 - 5x + 6 = 0$, $D = 25 - 24 = 1 > 0$, so roots are $2$ and $3$, which are real and distinct

Real and Equal Roots

• Occur when $D = 0$

• The quadratic curve touches the $x$-axis at one point

• Both roots are equal: $x_1 = x_2 = \frac{-b}{2a}$

Example: For $x^2 - 4x + 4 = 0$, $D = 16 - 16 = 0$, root = $2$

Complex Roots

• Occur when $D < 0$

• The quadratic curve does not intersect the $x$-axis

• Roots are complex conjugates: $p + iq$ and $p - iq$

Example: For $x^2 + x + 1 = 0$, $D = 1 - 4 = -3 < 0$, roots = $-\frac{1}{2} \pm \frac{\sqrt{3}}{2}i$

Special Cases of Roots

1. Rational and Irrational Roots ($D>0$)

   • If $a, b, c$ are rational:

     • $D$ is a perfect square → roots are rational

     • $D$ is not a perfect square → roots are irrational

2. Integer Roots ($a=1$, $b,c$ integers)

   • $D$ is a perfect square → roots are integers

   • $D$ is not a perfect square → roots are non-integer

How to Find the Nature of Roots

Step 1: Identify coefficients $a, b, c$ by comparing with $ax^2 + bx + c = 0$.
Step 2: Compute the discriminant: $D = b^2 - 4ac$.
Step 3: Determine the type of roots based on $D$:

• $D > 0$ → Real and unequal roots

• $D = 0$ → Real and equal roots

• $D < 0$ → Complex roots

Additional Classification for Rational/Irrational Roots:

Condition	Nature of Roots
$D>0$ and perfect square	Real, rational, and unequal
$D>0$ and not perfect square	Real, irrational, and unequal
$D>0$, perfect square, but $a$ or $b$ irrational	Irrational

Graphical Representation of Roots

The graphs of roots of a quadratic equation correspond to the points where the $y = ax^2 + bx + c$ intersects the $x$-axis:

• $D>0$: Graph crosses $x$-axis at two points (real and distinct roots)

• $D=0$: Graph touches $x$-axis at a single point (real and equal roots)

• $D<0$: Graph does not touch $x$-axis (complex roots)

Nature of Roots Depending on Coefficients

1. If $c = 0$ → one root = 0, other root = $-\frac{b}{a}$ : $x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \frac{-b \pm \sqrt{b^2}}{2a} = 0$ or $-\frac{b}{a}$

2. If $b = c = 0$ → both roots = 0

Sum, Product, and Difference of Roots

If $\alpha$ and $\beta$ are roots of $ax^2 + bx + c = 0$, then:

Sum of roots: $\alpha + \beta = \frac{-b}{a}$

Product of roots: $\alpha \cdot \beta = \frac{c}{a}$

Difference of roots: $\alpha - \beta = \left|\frac{\sqrt{D}}{a}\right|$

These formulas are essential for forming quadratic equations when roots are known.

Important Results Involving Roots

1. $\alpha^2 + \beta^2 = (\alpha + \beta)^2 - 2\alpha \beta$

2. $\alpha^2 - \beta^2 = (\alpha + \beta)(\alpha - \beta)$

3. $\alpha^3 + \beta^3 = (\alpha + \beta)^3 - 3\alpha\beta(\alpha + \beta)$

4. $\alpha^3 - \beta^3 = (\alpha - \beta)^3 + 3\alpha\beta(\alpha - \beta)$

Important Formulae related to Quadratic Equations

This section lists all the essential formulae for quadratic equations, including the quadratic formula, discriminant, sum and product of roots, and special cases, helping students quickly solve and analyze any quadratic problem.

Solved Examples Based on the Nature of Roots

Example 1: If $(1 + k) \tan^2 x - 4 \tan x - 1 - k = 0$ has real roots $\tan x_1$ and $\tan x_2$, where $\tan x_1 \ne \tan x_2$, then

1. $k^2 < 5,, k \ne -1$

2. $k^2 < 5$

3. $k^2 \leq 5,, k \ne -1$

4. none of these

Solution:

Condition for Real and Distinct Roots of Quadratic Equation -

$D = b^2 - 4ac > 0$ wherein

$ax^2 + bx + c = 0$

is the quadratic equation.

Since the given equation has distinct roots

$D > 0$

$16 + 4(1 - k^2) > 0$

$\Rightarrow k^2 < 5$

also $k \ne -1$

If $k = -1$ we will get only one solution, but we want two solutions

$\therefore k^2 < 5,, k \ne -1$

Hence, the answer is the option (1).

Example 2: If for $z = \alpha + i\beta$, $|z+2| = z + 4(1+i)$, then $\alpha + \beta$ and $\alpha \beta$ are the roots of the equation:

1. $x^2 + 3x - 4 = 0$

2. $x^2 + 7x + 12 = 0$

3. $x^2 + x - 12 = 0$

4. $x^2 + 2x - 3 = 0$

Solution:

$|z+2| = |\alpha + i\beta + 2| = \alpha + i\beta + 4 + 4i$

$\sqrt{(\alpha + 2)^2 + \beta^2} = (\alpha + 4) + i(\beta + 4)$

$(\alpha + 2)^2 + 16 = (\alpha + 4)^2$

$\beta + 4 = 0$

$\beta = -4$

$\alpha^2 + 4 + 4\alpha + 16 = \alpha^2 + 16 + 8\alpha$

$4 = 4\alpha$

$\alpha = 1$

$\alpha = 1,~\beta = -4$

$\alpha + \beta = -3,~\alpha\beta = -4$

Sum of roots $= -7$

Product of roots $= 12$

$x^2 + 7x + 12 = 0$

Hence, the answer is the option (2).

Example 3: If, for a positive integer n , the quadratic equation, $ \begin{aligned} & x(x+1)+(x+1)(x+2)+\ldots \\ & +(x+\overline{n-1})(x+n)=10 n \end{aligned} $ has two consecutive integral solutions, then $\boldsymbol{n}$ is equal to :
Solution:

Condition for Real and Distinct Roots of Quadratic Equation -

$
D=b^2-4 a c>0
$

wherein

$
a x^2+b x+c=0
$

is the quadratic equation

$
x(x+1)+(x+1)(x+2)+\ldots \ldots \ldots(x+(\overline{n-1}))(x+n)=10 n
$

$
\begin{aligned}
& \left(x^2+x\right)+\left(x^2+3 x+2\right)+\left(x^2+5 x+6\right)+\ldots \ldots \ldots\left[x^2+(n-1+n) x+n(n-1)\right]=10 n \\
& \Rightarrow \quad \sum x^2+\sum(n+n-1) x+\sum n(n-1)=10 n \\
& \Rightarrow n x^2+\sum(2 n-1) x+\sum\left(n^2-n\right)=10 n \\
& \Rightarrow n x^2+[n(n+1)-n] x+\left[\frac{n(2 n+1)(n+1)}{6}-\frac{n(n+1)}{2}\right]=10 n \\
& \Rightarrow n x^2+n^2 x+\left[\frac{n(n+1)(2 n+1-3)}{6}\right]=10 n \\
& \Rightarrow n x^2+n^2 x+\left[\frac{n(n+1)(n-1)}{3}\right]=10 n \\
& \Rightarrow x^2+n x+\frac{n^2-1}{3}=10 \\
& \Rightarrow x^2+n x+\frac{n^2-31}{3}=0 \\
& B^2-4 A C \geq 0 \\
& \therefore n^2-\frac{4}{3}\left(n^2-31\right) \geq 0 \\
& \therefore n^2 \leq 124
\end{aligned}
$
So maximum value $n$ is 11 .
Hence, the answer is 11 .

Example 4: Let $S = \left{ \alpha : \log_2 \left(9^{2\alpha-4} + 13\right) - \log_2 \left( \frac{5}{2} \cdot 3^{2\alpha-4} + 1 \right) = 2 \right}$. Then the maximum value of $\beta$ for which the equation $x^2 - 2\left( \sum_{\alpha \in S} \alpha \right)x + \sum_{\alpha \in S} (\alpha+1)^2 \beta = 0$ has real roots, is

1. 25

2. 24

3. 26

4. 27

Solution:

$\log_2 \left[ \frac{9^{2\alpha-4} + 13}{3^{2\alpha-4} \cdot \frac{5}{2} + 1} \right] = 2$

$9^{2\alpha-4} + 13 = 3^{2\alpha-4} \cdot \frac{5}{2} + 1 \cdot 4$

$= 3^{2\alpha-4} \cdot \frac{5}{2} + 4$

$= 3^{2\alpha-4} \cdot 5 + 13 = 10 \cdot 3^{2\alpha-4} + 4$

Let $t = 3^{2\alpha-4}$

$t^2 - 10t + 9 = 0$

$t = 1, 9$

$3^{2\alpha-4} = 3^0, 3^2$

$2\alpha - 4 = 0, 2$

$\alpha = 2, 3$

$\sum \alpha = 2 + 3 = 5$

$x^2 - 2(5)x + 25\beta = 0$

$D \geq 0$

$(2)^2 (25) - 4(25)(\beta) \geq 0$

$\beta \leq 25$

$\beta_{\max} = 25$

Hence, the answer is the option 1.

Example 5: Equation $3 x^2+6 x+2=0$ will have

1) Real & Equal roots

2) Real & Distinct roots

3) Imaginary roots

4) Can't be determined

Solution:

Condition for Real and Distinct Roots of Quadratic Equation -

$
\begin{aligned}
& D=b^2-4 a c>0 \\
& \text { - wherein } \\
& a x^2+b x+c=0
\end{aligned}
$

is the quadratic equation

$
D=(6)^2-4(3)(2)=36-24=12>0
$
Hence, the answer is the option 2.

List of Topics related to Nature of roots of Quadratic Equations

Explore the essential topics related to the nature of roots of quadratic equations, including discriminant, real and complex roots, equal roots, and the relationship between roots and coefficients. This section helps students focus on key areas for better understanding and exam preparation.

NCERT Resources

Access comprehensive NCERT resources for quadratic equations, including detailed notes, solved examples, and exemplar problems, to strengthen your conceptual clarity and practice effectively.

• NCERT Maths Notes for Class 11th Chapter 4 - Complex Numbers and Quadratic Equations

• NCERT Maths Solutions for Class 11th Chapter 4 - Complex Numbers and Quadratic Equations

• NCERT Maths Exemplar Solutions for Class 11th Chapter 4 - Complex Numbers and Quadratic Equations

Practice Questions based on Nature of roots of Quadratic Equations

Sharpen your problem-solving skills with a curated set of practice questions on the nature of roots of quadratic equations, designed to boost accuracy and confidence for school exams and competitive tests.

Nature Of Roots Depending Upon Coefficients And Discriminant - Practice Question MCQ

We have shared below the list of practice questions on related topics: