Argument of Complex Numbers - Definition, Formula, Example
The argument of a complex number is the angle that shows the direction of the number in the Argand plane. It is written as $\arg(z)$ and helps to understand the position of a complex number using trigonometry. Along with the modulus, the argument is an important part of the polar form of complex numbers and is widely used in mathematics and geometry. In this article, we will learn the definition, formula, quadrant rules, properties, and solved examples of the argument of a complex number.
This Story also Contains
- What are Complex Numbers?
- Argument of Complex Numbers Definition
- How to Find the Argument of Complex Numbers?
- Argument of a complex number in different quadrants
- Properties of Argument of Complex Numbers
- Applications Of Argument Of Complex Number
- List of topics related to the Argument of a Complex Number
- NCERT Resources
- Practice Questions based on the Argument of a Complex Number
What are Complex Numbers?
A complex number is a number that can be written in the form $a+ib$, where $a$ is the real part, $b$ is the imaginary part, and $i=\sqrt{-1}$. Complex numbers are represented in the Argand plane, with the real part on the x-axis and the imaginary part on the y-axis.
For example, $z=5+2i$ is a complex number where $\operatorname{Re}(z)=5$ and $\operatorname{Im}(z)=2$.
Argument of Complex Numbers Definition
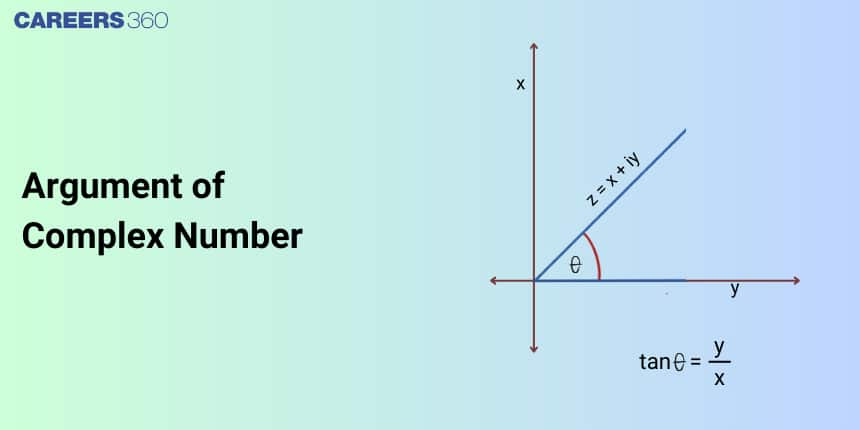
The argument of a complex number is the angle made by the line joining the origin to the point $(x,y)$ in the Argand plane, measured with respect to the positive x-axis.
For a complex number $z=x+iy$, the argument is denoted as $\arg(z)$ or $\theta$. It represents the direction of the vector corresponding to $z$ in the complex plane.
Argument of Complex Numbers Formula
If a complex number $z=x+i y$ is represented by a point $P$ in the Argand plane and $O P$ forms some angle with a positive x-axis, let's denote it with $\theta$, then $\theta$ is called the argument of z.

$\begin{aligned} & \tan \theta=\frac{\mathrm{PM}}{\mathrm{OM}} \\ & \tan \theta=\frac{\mathrm{y}}{\mathrm{x}}=\frac{\operatorname{Im}(\mathrm{z})}{\operatorname{Re}(\mathrm{z})} \Rightarrow \theta=\tan ^{-1} \frac{\mathrm{y}}{\mathrm{x}} \\ & \arg (\mathrm{z})=\theta=\tan ^{-1} \frac{\mathrm{y}}{\mathrm{x}}\end{aligned}$
Principle Argument Of Complex Number = -π < θ < π
The principal argument of a complex number lies in the interval $-\pi < \theta < \pi$. For the first and second quadrants: $0 < \theta < \pi$ (measured anticlockwise). For the third and fourth quadrants: $-\pi < \theta < 0$ (measured clockwise). Further, the general argument of the complex number is $2 n \pi+\theta$.
General Argument Of Complex Number = 2nπ + θ
The general argument is expressed as: $\arg(z) = 2n\pi + \theta$, where $n$ is any integer.
Principal Argument vs General Argument
The principal argument of a complex number is the unique angle $\theta \in (-\pi, \pi]$.
The general argument includes all angles: $\theta + 2n\pi$, where $n \in \mathbb{Z}$.
Relationship Between Argument and Modulus
In polar form, a complex number is written as $z = r(\cos \theta + i \sin \theta)$, where $r = |z|$ is the modulus and $\theta = \arg(z)$. The modulus defines the length, and the argument defines the angle.
How to Find the Argument of Complex Numbers?
To calculate the argument of a complex number:
Identify real part ($x$) and imaginary part ($y$).
Substitute values in $\theta = \tan^{-1}\left(\frac{y}{x}\right)$.
Adjust $\theta$ based on the quadrant where $(x,y)$ lies.
Argument of a complex number in different quadrants
If $\theta$ lies between $-\pi<\theta \leq \pi$, then $\theta$ is called a principal argument. The value of the argument differs depending on which quadrant point $(x, y)$ lies.
First Quadrant: $\arg(z) = \tan^{-1}\left(\frac{y}{x}\right)$ (acute angle).
Second Quadrant: $\arg(z) = \pi - \tan^{-1}\left(\frac{y}{|x|}\right)$ (obtuse positive angle).
Third Quadrant: $\arg(z) = -\pi + \tan^{-1}\left(\frac{y}{x}\right)$ (obtuse negative angle).
Fourth Quadrant: $\arg(z) = -\tan^{-1}\left(\frac{|y|}{x}\right)$ (negative acute angle).
Note:
If $\arg (\mathrm{z})=\frac{\pi}{2}$ or $-\frac{\pi}{2}, \mathrm{z}$ is purely imaginary.
If $\arg (\mathrm{z})=0$ or $\pi, \mathrm{z}$ is purely real.
Properties of Argument of Complex Numbers
i) Argument of product
$\arg (z_1 z_2) = \arg (z_1) + \arg (z_2) + 2k\pi, ; k \in \mathbb{Z}$
Explanation: The angle of the product of two complex numbers equals the sum of their individual angles, adjusted by multiples of $2\pi$.
ii) Argument of quotient
$\arg \left(\frac{z_1}{z_2}\right) = \arg (z_1) - \arg (z_2) + 2k\pi, ; k \in \mathbb{Z}$
Explanation: The angle of the quotient of two complex numbers equals the difference of their arguments.
iii) Argument of conjugate
$\arg (\bar{z}) = -\arg (z)$
Explanation: The conjugate of a complex number reflects it across the real axis in the Argand plane, so its angle changes sign.
iv) Argument of powers
$\arg (z^n) = n \cdot \arg (z) + 2k\pi, ; k \in \mathbb{Z}$
Explanation: Raising a complex number to a power multiplies its angle by $n$
v) Equal arguments condition (collinear vectors in same direction)
If $|z_1 + z_2| = |z_1| + |z_2|$, then
$\arg (z_1) = \arg (z_2)$
Explanation: This condition means $z_1$ and $z_2$ lie along the same line in the Argand plane, pointing in the same direction.
vi) Opposite arguments condition (collinear vectors in opposite direction)
If $|z_1 + z_2| = \big||z_1| - |z_2|\big|$, then
$\arg (z_1) - \arg (z_2) = \pi$
Explanation: This means $z_1$ and $z_2$ are collinear but point in opposite directions on the Argand plane.
Applications Of Argument Of Complex Number
The argument of a complex number has numerous applications in transforming the complex number to polar form, and also in finding the relationship between the real part and the imaginary part of the complex number.
Polar Form of Complex Number: The polar form of the complex number is P = r(Cosθ + iSinθ). Here θ is the argument of the complex number, and r is the argument of the complex number. Polar form is another important form of representing the complex number in the argand plane. The polar form of the complex number represented in cartesian form is (rCosθ, rSinθ).
Solved Examples Based on Argument of a Complex Number
Example 1: Arg $\left(\frac{2 i}{\sqrt{3}-i}\right)$ equals:
Solution:
As we have learned in Definition of Argument/Amplitude of z in Complex Numbers:
$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$
$\theta, \pi-\theta,-\pi+\theta,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant respectively.
Now,
$\begin{aligned} & \frac{2 i}{\sqrt{3}-i}=\frac{2 i}{\sqrt{3}-i} \times \frac{\sqrt{3}+i}{\sqrt{3}+i}=\frac{2 \sqrt{3} i-2}{4} \\ & \Rightarrow \frac{2 i}{\sqrt{3}-i}=\frac{-1}{2}+\frac{i \sqrt{3}}{2}\end{aligned}$
$\because$ it lies in 2nd quadrant so
argument= $\pi-\tan ^{-1}\left|\frac{\frac{\sqrt{3}}{2}}{\frac{-1}{2}}\right|=\pi-\frac{\pi}{3}=\frac{2 \pi}{3}$
Hence, the required answer is $\frac{2 \pi}{3}$.
Solution:
Definition of Argument/Amplitude of z in Complex Numbers -
$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$
$\theta, \pi-\theta,-\pi+\theta,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant respectively.
$z=(1)^{\frac{1}{3}} \Rightarrow z=\cos \frac{2 k \pi}{3}+i \sin \frac{2 k \pi}{3}$
k=0,1,2 so z gives three roots
$\Rightarrow 1, \frac{-1}{2}+i \frac{\sqrt{3}}{2}(\omega), \frac{-1}{2}-i \frac{\sqrt{3}}{2}\left(\omega^2\right)$
- wherein
$\omega=\frac{-1}{2}+\frac{i \sqrt{3}}{2}, \omega^2=\frac{-1}{2}-\frac{i \sqrt{3}}{2}, \omega^3=1,1+\omega+\omega^2=0$
$1, \omega, \omega^2$ are cube roots of unity.
$x^2+x+1=0$, roots are, $\omega$ and $\omega^2$ where $\omega$ is the cube root of unity.
$
z=3+6 i\left(z_0\right)^{81}-3 i\left(z_0\right)^{90}
$
$z_0=\omega$ and $\omega^2$
$
\begin{aligned}
& z=3+6 i(\omega)^{81}-3 i(\omega)^{93} \\
& z=3+3 i \quad \because \omega^3=1 \\
& \arg (z)=\frac{1}{4}
\end{aligned}
$
Hence, the required answer is $\frac{\pi}{4}$.
Example 3: Which of the following is one of the arguments of $z=-\sqrt{3}-3 i$:
1) $\frac{\pi}{3}$
2) $\frac{-5 \pi}{3}$
3) $\frac{-4 \pi}{3}$
4) $\frac{4 \pi}{3}$
Solution:
As we have learned in, General Argument of a Complex Number: $2 n \pi+0$
- wherein
$\theta$ is the principal argument of complex numbers.
$\because$ z lies in 3rd quadrant
$\therefore$ its principal argument $=-\pi+\tan ^{-1}\left|\frac{-3}{-\sqrt{3}}\right|=-\pi+\tan ^{-1} \sqrt{3}=-\pi+\frac{\pi}{3}=\frac{-2 \pi}{3}$
$\therefore 2 n \pi-\frac{2 \pi}{3}$ will be its general argument.
for n=1, we get argument = $\frac{4 \pi}{3}$
Hence, the required answer is the option (4).
Solution:
Definition of Argument/Amplitude of $z$ in Complex Numbers -
$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$
$\theta, \pi-\theta,\pi+\theta,-\theta$ are Principal Argument if $z$ lies in first, second, third or fourth quadrant respectively.
$\arg (z-i+2)=\frac{\pi}{6} \Rightarrow \tan \frac{\pi}{6}=\frac{y-1}{x+2}$
$\Rightarrow x-\sqrt{3 y}=-(\sqrt{3}+2), x>-2, y>1$
$\arg (z+4-3 i)=-\frac{\pi}{4} \Rightarrow \tan \left(-\frac{\pi}{4}\right)=\frac{y-3}{x+4}$
$\Rightarrow y+x=-1, x>-4, y<3$
So, there is no point of intersection.
Example 5: Arg $\left(i^{18}+\frac{1}{i^{25}}\right)$ equals:
Solution:
$i^{18}+\frac{1}{i^{25}}=\left(i^4\right)^4 \cdot i^2+\left(\frac{1}{i^4}\right)^6 \cdot \frac{1}{i}=i^2+\frac{1}{i}=-1-i$
As this lies in the third quadrant, so Arg(z) = $-\pi+\tan ^{-1} \left\lvert\, \frac{y}{x}\right.$
$\therefore$ Arg $(-1-i)=-\pi+\tan ^{-1}\left|\frac{-1}{-1}\right|=-\pi+\frac{\pi}{4}=\frac{-3 \pi}{4}$
Hence, the required answer is $\frac{-3 \pi}{4}$.
List of topics related to the Argument of a Complex Number
Below is the list of important concepts connected with the argument of a complex number, including its definition, formulas, properties, quadrant-wise cases, and applications. These topics provide a complete understanding of how arguments work in complex number geometry.
NCERT Resources
Below are the key NCERT resources for Class 11 Maths Chapter 5 – Complex Numbers and Quadratic Equations, including step-by-step NCERT solutions, exemplar problems with detailed explanations, and concise notes to strengthen understanding and practice.
NCERT Solutions for Class 11 Maths Chapter 5 -Complex Numbers and Quadratic Equations
NCERT Exemplar Class 11 Maths Solutions for Chapter 5 - Complex Numbers and Quadratic Equations
NCERT Class 11 Maths Notes for Chapter 5 - Complex Numbers and Quadratic Equations
Practice Questions based on the Argument of a Complex Number
Below are carefully chosen practice questions on the argument of a complex number. These questions will help you apply formulas, understand quadrant-wise cases, and strengthen problem-solving skills for exams.
Argument Of Complex Number - Practice Question MCQ
We have shared practice questions sets for related topics below:
Frequently Asked Questions (FAQs)
The two important properties of the argument of a complex number are as follows:
$\arg(z_1 z_2) = \arg(z_1) + \arg(z_2)$
$\arg\left(\frac{z_1}{z_2}\right) = \arg(z_1) - \arg(z_2)$
The modulus of a complex number gives the distance of the point representing the number from the origin, and the argument gives the inclination of the complex number in the Argand plane.
For a complex number $z = a + ib$:
Modulus: $|z| = \sqrt{a^2 + b^2}$
Argument: $\theta = \tan^{-1}\left(\frac{b}{a}\right)$
The argument is $\tan ^{-1} \frac{x}{y}$
Principal arguments of a complex number always lie between -180 degrees to 180 degrees.
Arguments of complex numbers mean the angle made by complex numbers with origin in the argand plane.



