Rotation Of Complex Numbers
Rotation of complex numbers is a key concept in mathematics where multiplication by a complex number causes a point in the plane to rotate around the origin while maintaining its distance from the origin (magnitude). This geometric transformation changes the angle (argument) of the complex number without affecting its size in mathematics. In this article, we will explore the basics of rotation of complex numbers, their mathematical properties.
This Story also Contains
- What is Rotation of Complex Numbers?
- Important Terminologies of Complex Numbers
- Properties of Rotation in Complex Numbers
- Rotation Theorems and Formulas
- List of topics related to the Rotation Of Complex Numbers
- NCERT Resources
- Practice Questions based on the Rotation Of Complex Numbers
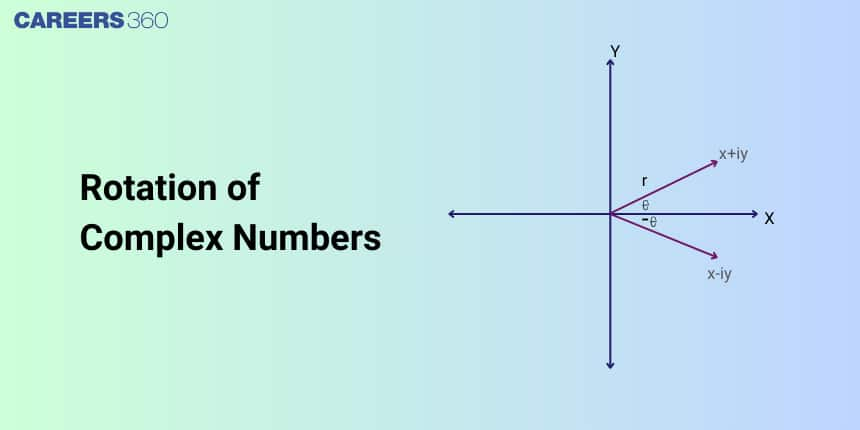
What is Rotation of Complex Numbers?
Rotation of complex numbers occurs when a complex number is multiplied by another complex number having a magnitude of 1. This multiplication changes the angle (or argument) of the original number without altering its magnitude. In simple terms, the resulting complex number is a rotated version of the original around the origin in the complex plane.
Geometric Interpretation on Argand Plane
Every complex number $z = x + iy$ can be represented as a point $(x, y)$ in the Argand plane. When we multiply $z$ by a complex number $w = \cos \phi + i \sin \phi$ (which has magnitude 1), the point rotates by an angle $\phi$ about the origin. The rotated complex number $z'$ is given by:
$z' = z \times w = r(\cos \theta + i \sin \theta) \times (\cos \phi + i \sin \phi) = r(\cos(\theta + \phi) + i \sin(\theta + \phi))$
where $r$ is the magnitude and $\theta$ is the argument of $z$.
This rotation preserves the distance from the origin, making it a length-preserving transformation useful in mathematical and engineering problems.
Vector Notation
Let us take any complex number $\mathrm{z}={x}+\mathrm{i} y$, so point $\mathrm{P}(\mathrm{x}, \mathrm{y})$ represents it on the Argand Plane. Then OP can be represented as a vector $\overrightarrow{O P}=x \hat{i}+y \hat{j}$, where $\hat{i}$ represents the x -axis while $\hat{j}$ represents the y -axis and O is the origin.

Therefore, the complex number z can be represented as $\overrightarrow{O P}$
Similarly, a vector starting from point $A\left(z_1\right)$ and ending at $B\left(z_2\right)$ is represented by $A B$ vector which equals $\left(z_2-z_1\right)$
The length of $A B$ is given by the modulus of this vector $\left|z_2-z_1\right|$
Rotation Theorem (Coni Method)

We know the angle $\theta$. Our purpose is to write down an expression that relates all the four quantities $z_1, z_2, z_3$, and $\theta$.
Consider the vector $z_3-z_2$. Let its argument be $\theta_1$. Similarly, let the argument of the vector $z_1-z_2$ be $\theta_2$. Now, a little thought will show us that $\theta$ is simply:
$
\theta=\theta_1-\theta_2
$
Now, we write $z_3-z_2$ and $z_1-z_2$ in Euler's form:
$
\begin{aligned}
& z_3-z_2=\left|z_3-z_2\right| e^{i \theta_1} \\
& z_1-z_2=\left|z_1-z_2\right| e^{i \theta_2}
\end{aligned}
$
Since we know $\theta_1-\theta_2$, we divide equation (1) by equation (2) to get:
$
\frac{z_3-z_2}{z_1-z_2}=\frac{\left|z_3-z_2\right|}{\left|z_1-z_2\right|} e^{i \theta}
$
This is the relation we were looking for. It relates all the four terms $z_1, z_2, z_3$ and $\theta$.
We are given the vector $z_1-z_2$. We need to modify it into the vector $z_3-z_2$.
Obviously, there will be a change in modulus. Apart from that, we need to rotate the vector $z_1-z_2$ anticlockwise by angle $\theta$ too. This is where the term rotation comes from.
Viewing the process in this way, we obtain relation (3) as follows:
1. Write down the unit vector in the direction of the original vector, the one that we need to rotate:
$
\frac{z_1-z_2}{\left|z_1-z_2\right|}
$
2. To rotate this unit vector by an angle $\theta$ (anticlockwise; for clockwise, it will be $-\theta$ ), we multiply it by $e^{i \theta}$.
For the current case, this turns the unit vector into a new unit vector along the direction of the vector $z_3-z_2$ :
$
\frac{z_1-z_2}{\left|z_1-z_2\right|} e^{i \theta}
$
3. Finally, to turn this unit vector into the final vector that we need to obtain after rotation, we multiply the unit vector by the appropriate magnitude.
Thus, we obtain the required final vector after rotation:
$
z_3-z_2=\left|z_3-z_2\right| \cdot \frac{z_1-z_2}{\left|z_1-z_2\right|} e^{i \theta}
$
This is the same relation that we obtained in equation (3).
Using this same approach, suppose that we now wish to relate four complex numbers in the following configuration
Using rotation, we can obtain the vector $z_1-z_2$ from the vector $z_4-z_3$ :
- Unit vector along $z_4-z_3$ direction:
$
\frac{z_4-z_3}{\left|z_4-z_3\right|}
$
(Initial unit vector)
- Unit vector along $z_1-z_2$ direction:
$
\frac{z_1-z_2}{\left|z_1-z_2\right|}
$
(Final unit vector)
- Angle between the two: $\theta$
Thus, we get the final relation:
$
\frac{z_1-z_2}{\left|z_1-z_2\right|}=\frac{z_4-z_3}{\left|z_4-z_3\right|} e^{i \theta}
$
This is the relation we wished to obtain.
Note: The final vector should be in the numerator and the starting vector in the denominator. $\theta$ is positive if rotation is anti-clockwise and negative if it is clockwise.
Important Terminologies of Complex Numbers
This section covers the basic operations on complex numbers, including addition, subtraction, multiplication, and division, along with different forms like rectangular and polar. Understanding these operations and forms is essential for mastering complex number calculations in algebra and geometry.
Polar and Euler’s Form of Complex Numbers
A complex number $z = x + iy$ can be expressed in polar form as
$z = r(\cos \theta + i \sin \theta)$
where $r = |z| = \sqrt{x^2 + y^2}$ is the magnitude (or modulus) of $z$, and $\theta = \arg(z) = \tan^{-1}\frac{y}{x}$ is the argument (or angle) of $z$.
Euler’s formula simplifies this to $z = r e^{i \theta}$
which is widely used for easy manipulation of complex numbers, especially in rotation and signal processing applications.
Magnitude and Argument of Complex Numbers
The magnitude $r$ represents the distance of the complex number from the origin in the Argand plane. The argument $\theta$ is the angle made with the positive real axis. These two values fully describe the position of the complex number in polar coordinates, making it convenient to perform geometric transformations.
Multiplication and Rotation Relationship
Multiplying two complex numbers involves multiplying their magnitudes and adding their arguments:
$z_1 \times z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)}$
Hence, when we multiply a complex number by another complex number of magnitude 1 (a unimodular complex number), we effectively rotate the first number by the argument of the second without changing its magnitude. This property forms the mathematical basis of rotation in the complex plane.
Properties of Rotation in Complex Numbers
We have provided the key properties of rotation in complex numbers, explaining how multiplication by a unimodular complex number results in a pure rotation on the Argand plane.
Rotation by Multiplying with Unimodular Complex Numbers
A unimodular complex number has magnitude 1, i.e., $|w| = 1$. Multiplying any complex number $z$ by such a $w$ results in a rotation by angle $\arg(w)$ on the Argand plane:
$z' = z \times w = r e^{i(\theta + \phi)}$
where $\phi = \arg(w)$.
Effect of Multiplying by $i$, $-1$, and Powers of $i$
Multiplying by $i$ rotates a complex number by $90^\circ$ (or $\pi/2$ radians) counterclockwise.
Multiplying by $-1$ rotates the number by $180^\circ$.
Powers of $i$ produce rotations of multiples of $90^\circ$:
$i^1 = e^{i \pi/2}, \quad i^2 = e^{i \pi}, \quad i^3 = e^{i 3\pi/2}, \quad i^4 = 1$
Preservation of Magnitude and Change in Argument
During rotation by multiplication of unimodular complex numbers, the magnitude $|z|$ remains unchanged while the argument increases by the angle of rotation:
$∣z′∣=∣z∣,arg(z′)=arg(z)+\text{rotation angle}$
Rotation Theorems and Formulas
We have provided the essential rotation theorems and formulas that explain how complex numbers represent geometric rotations on the Argand plane. These theorems establish that multiplying by a unit complex number rotates points by the argument angle while preserving magnitude.
Rotation Theorem for Vectors in Complex Plane
If $z_1$ and $z_2$ are two complex numbers with the same magnitude, the argument of their quotient gives the rotation angle between them:
$\theta = \arg\left(\frac{z_1}{z_2}\right)$
Expression for Rotated Complex Number
The rotated complex number $z'$ after rotation by angle $\phi$ is:
$z' = z e^{i \phi}$
Examples Demonstrating Rotation
Rotating $z = 1 + i$ by $90^\circ$ using multiplication by $i$:
$z' = (1 + i) \times i = i + i^2 = i - 1 = -1 + i$
Rotation by $180^\circ$ using $-1$:
$z' = (3 + 4i) \times (-1) = -3 - 4i$
These examples demonstrate how multiplication corresponds to rotation on the complex plane.
Solved Examples Based On the Rotation of Complex Numbers
Solution:
As we have learned in,
Rotation -
$
\frac{z_3-z_1}{z_2-z_1}=\frac{\left|z_3-z_1\right|}{\left|z_2-z_1\right|} \cdot e^{i \Theta}
$
wherein
$
e^{i \theta}=\cos \theta+i \sin \theta
$
using rotation at 0
$
\frac{Z_2-0}{Z_1-0}=\frac{2 \sqrt{2}}{\sqrt{2}} e^{i 3 \frac{\pi}{2}}
$
$
\Rightarrow \frac{Z_2}{Z_1}=2(-i) \Rightarrow Z_2=-2 i(1+i)=2-2 i
$
Hence, the answer is 2-2i.
Example 2: Let $z_1$ and $z_2$ be two roots of the equation $z^2+a z+b=0, z$ being complex further, assume that the origin, $z_1$ and $z_2$ form an equilateral triangle then
1) $a^2=2 b$
2) $a^2=3 b$
3) $a^2=4 b$
4) $a^2=b$
Solution:
As we have learned,
Rotation -
$
\frac{z_3-z_1}{z_2-z_1}=\frac{\left|z_3-z_1\right|}{\left|z_2-z_1\right|} \cdot e^{i \Theta}
$
- wherein
$
e^{i \theta}=\cos \theta+i \sin \theta
$
$
\begin{aligned}
& z_1+z_2=-a \\
& z_1 z_2=b
\end{aligned}
$
we have,
$
\begin{aligned}
& \frac{z_1}{z_2}=\frac{\left|z_1\right|}{\left|z_2\right|} e^{i \pi / 3} \\
& =\frac{1}{1} e^{i \pi / 3}
\end{aligned}
$
$
\begin{aligned}
& z_1=z_2 e^{i \pi / 3} \\
& \Rightarrow z_2\left(e^{i \pi / 3}+1\right)=-a \\
& \text { and } \Rightarrow z_2^2\left(e^{i \pi / 3}\right)=b \\
& \therefore b e^{-i \pi / 3}=\frac{a^2}{\left(1+e^{i \pi / 3}\right)^2}
\end{aligned}
$
$
\begin{aligned}
& \Rightarrow a^2=b\left(1+e^{i 2 \pi / 3}+2 e^{i \pi / 3}\right) e^{-i \pi / 3} \\
& =b\left(e^{-i \pi / 3}+e^{i(2 \pi-\pi) / 3}+2\right)=b\left(e^{-i \pi / 3}+e^{i \pi / 3}+2\right)=b(2 \cos \pi / 3+2)=3 b
\end{aligned}
$
Hence, the answer is the option 2.
Example 3: $A\left(z_1\right), B\left(z_2\right), O(O)$ are vertices of a right-angled isosceles triangle, right-angled at 0 then ( $z_1-i . z_2$ ) equals
Solution: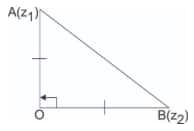
Rotation on $\angle A O B$
$\frac{Z_1-0}{Z_2-0}=\frac{\left|Z_1-0\right|}{\left|Z_2-0\right|} \cdot e^{\frac{t \pi}{2}}$
$\frac{Z_1-0}{Z_2-0}=\frac{\left|Z_1-0\right|}{\left|Z_2-0\right|}\left(\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right)$
$\Rightarrow \frac{Z_1}{Z_2}=\frac{O A}{O B} \cdot i$
$\Rightarrow Z_1=i Z_2$
Hence, the correct answer is 0.
1) $\arg z_2=\pi-\tan ^{-1} 3$
2) $\arg \left(z_1-2 z_2\right)=-\tan ^{-1} \frac{4}{3}$
3) $\left|z_2\right|=\sqrt{10}$
4) $\left|2 z_1-z_2\right|=5$
Solution:
$A B=A O \quad Z^{-i \pi / 2}=-2+i$
So $O B=(-2+i)+(1+2 i)$
$Z_2=-1-3 i$
$\therefore\left|2 Z_1-Z_2\right|=\sqrt{10}$
Example 5: The line joining the origin and the point represented by $\mathrm{z}=1+\mathrm{i}$ is rotated through an angle $\frac{\pi}{2}$ in an anticlockwise direction about the origin and stretched by additional $\sqrt{3}$ units. The new position of the point is:
1) $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{2}}(-1+\mathrm{i})$
2) $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{2}}(1-\mathrm{i})$
3) $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{2}}(-1-\mathrm{i})$
4) $\frac{\sqrt{3}+\sqrt{2}}{\sqrt{2}}(1+\mathrm{i})$
Solution:
As we have learned in the Rotation Theorem (Coni Method)
Now,
Now,
Let initial point be $\mathrm{A}(1+\mathrm{i})$, O be origin $(0+0 \mathrm{i})$, and $\mathrm{B}(\mathrm{z})$ be the final point
$
|A O|=\sqrt{2}
$
And length of OB is $\sqrt{3}$ more than $|\mathrm{AO}|$, so $|\mathrm{BO}|=\sqrt{2}+\sqrt{3}$
Now using the Rotation Theorem
$
\begin{aligned}
& \frac{O B}{O A}=\frac{|O B|}{|O A|} \cdot e^{\frac{i \pi}{2}} \\
& \frac{z-0}{1+i-0}=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}} e^{\frac{i \pi}{2}} \\
& z=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}} \cdot(1+i) \cdot e^{\frac{i \pi}{2}} \\
& z=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}} \cdot(1+i) \cdot(\cos (\pi / 2)+i \sin (\pi / 2)) \\
& z=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}} \cdot(1+i) \cdot i \\
& z=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{2}} \cdot(-1+i)
\end{aligned}
$
Hence, the answer is the option 1
List of topics related to the Rotation Of Complex Numbers
Rotation of complex numbers helps in understanding their transformation on the Argand plane through magnitude and direction, closely connected to trigonometric form, roots of unity, and geometric interpretation. Below are some of the important topics related to this concept.
NCERT Resources
This section provides NCERT solutions, exemplar problems, and revision notes for Class 11 Maths Chapter 5 on Complex Numbers and Quadratic Equations. These resources help in strengthening concepts and preparing effectively for exams.
NCERT Solutions for Class 11 Maths Chapter 5 -Complex Numbers and Quadratic Equations
NCERT Exemplar Class 11 Maths Solutions for Chapter 5 - Complex Numbers and Quadratic Equations
NCERT Class 11 Maths Notes for Chapter 5 - Complex Numbers and Quadratic Equations
Practice Questions based on the Rotation Of Complex Numbers
This section offers practice questions based on the Rotation of Complex Numbers to test understanding and improve problem-solving skills. These exercises are designed to strengthen concepts and support exam preparation.
Rotation Of Complex Numbers - Practice Question MCQ
We have shared practice question sets for related topics below:
