What is the general formula for finding the square root of a complex number?

For a complex number z = a + bi, its square roots can be found using the formula: ±(√((a + √(a² + b²))/2) + i * sign(b) * √((√(a² + b²) - a)/2)).

How do you interpret the square root of a negative real number in the complex plane?

The square root of a negative real number -a (where a > 0) is an imaginary number ±i√a. Geometrically, this represents points on the imaginary axis of the complex plane.

What is the difference between principal square root and general square root of a complex number?

The principal square root of a complex number is the one with a non-negative real part (or positive imaginary part if the real part is zero). The general square root includes both the principal square root and its negative.

Why do complex numbers always have two square roots?

Complex numbers always have two square roots because squaring a complex number doesn't change its angle in the complex plane, only doubles it. So, there are always two numbers that, when squared, give the same result: one with half the angle, and one with half the angle plus π.

How does finding the square root of a complex number relate to solving quadratic equations?

Finding square roots of complex numbers is crucial in solving quadratic equations with complex coefficients or when the discriminant is negative, leading to complex roots.

How is De Moivre's formula related to finding square roots of complex numbers?

De Moivre's formula can be used to find square roots of complex numbers in polar form. If z = r(cos θ + i sin θ), then its square roots are ±√r(cos(θ/2) + i sin(θ/2)).

Why can't we use the same method for finding square roots of real numbers to find square roots of complex numbers?

The method for real numbers doesn't work directly for complex numbers because complex numbers involve two components (real and imaginary). We need to consider both parts simultaneously and use more advanced techniques like completing the square or polar form.

How does the concept of branch cuts relate to square roots of complex numbers?

Branch cuts are lines in the complex plane where a multi-valued function like the square root is discontinuous. For the square root function, the standard branch cut is along the negative real axis, allowing us to define a single-valued "principal" square root function.

How does the absolute value of a complex number relate to its square root?

If z is a complex number and w is its square root, then |w| = √|z|. This means the absolute value of the square root is the square root of the absolute value of the original number.

What is the geometric interpretation of square roots of complex numbers?

Geometrically, if z is represented as a point in the complex plane, its square roots are two points that lie on the angle bisectors of the angle formed by z and the positive real axis, at a distance of √|z| from the origin.

Can every complex number have a square root?

Yes, every complex number has a square root. In fact, every non-zero complex number has exactly two square roots, which are negatives of each other.

Why does i have two square roots?

Like any non-zero complex number, i has two square roots because there are two complex numbers that, when squared, give i. These are (1 + i)/√2 and -(1 + i)/√2.

How do you find the square root of a purely imaginary number?

To find the square root of a purely imaginary number bi, we can use the formula ±√(|b|/2) * (1 + i) if b > 0, or ±√(|b|/2) * (1 - i) if b < 0. This results in a complex number with equal real and imaginary parts.

What is the relationship between the square roots of i and -i?

The square roots of i are (1 + i)/√2 and -(1 + i)/√2, while the square roots of -i are (1 - i)/√2 and -(1 - i)/√2. These are complex conjugates of each other.

How do you find the square root of a complex number in polar form?

If z = r(cos θ + i sin θ) is in polar form, its square roots are ±√r(cos(θ/2) + i sin(θ/2)). This involves halving the angle and taking the square root of the modulus.

What is the relationship between complex conjugates and square roots of complex numbers?

If w is a square root of z, then the complex conjugate of w is a square root of the complex conjugate of z. This property helps in finding both square roots once one is known.

How do you verify if a given complex number is indeed a square root of another complex number?

To verify if w is a square root of z, square w and check if it equals z. Remember to multiply both the real and imaginary parts: (a + bi)² = (a² - b²) + (2ab)i.

What is the significance of i^(1/2) in the context of square roots of complex numbers?

i^(1/2) represents the square root of i, which is (1 + i)/√2. This is a fundamental result in complex number theory and is often used in more advanced calculations involving complex roots.

How does the concept of principal value apply to square roots of complex numbers?

The principal value of the square root of a complex number is the one with a non-negative real part, or with a positive imaginary part if the real part is zero. This convention helps in defining a single-valued square root function.

What happens to the square root of a complex number when you rotate the original number by 360 degrees?

Rotating a complex number by 360 degrees doesn't change it, but rotating its square root by 360 degrees gives you the negative of the original square root. This is because a 360-degree rotation of the square root corresponds to a 720-degree rotation of the original number.

How do you find the square root of a complex number without using a calculator?

For simple complex numbers, you can use algebraic methods like completing the square. For example, to find √(3 + 4i), assume (a + bi)² = 3 + 4i, expand, and solve the resulting system of equations.

What is the relationship between the arguments of a complex number and its square roots?

If θ is the argument of a complex number z, then the arguments of its square roots are θ/2 and (θ + 2π)/2. This is because multiplying complex numbers adds their arguments, so halving the argument gives the square root.

How does the concept of square roots extend to higher roots of complex numbers?

The concept extends similarly: an nth root of a complex number z is a number w such that w^n = z. Unlike square roots which always come in pairs, a complex number has n distinct nth roots for any positive integer n.

What is the connection between Euler's formula and square roots of complex numbers?

Euler's formula (e^(iθ) = cos θ + i sin θ) is crucial in expressing complex numbers in polar form, which simplifies the process of finding square roots, especially when using De Moivre's formula.

How do you graphically represent the square roots of a complex number on an Argand diagram?

On an Argand diagram, the square roots of a complex number z are represented by two points. These points lie on a circle centered at the origin with radius √|z|, and their arguments are half the argument of z and half the argument of z plus π.

What is the significance of the discriminant in finding square roots of complex numbers?

The discriminant, typically used in quadratic equations, also plays a role in complex square roots. When the discriminant is negative, it indicates that the square roots are non-real complex numbers.

How does the concept of analytic continuation relate to square roots of complex numbers?

Analytic continuation allows us to extend the definition of square root from positive real numbers to the complex plane. This extension requires careful consideration of branch cuts to ensure a well-defined function.

What is the relationship between logarithms and square roots of complex numbers?

The square root of a complex number z can be expressed using complex logarithms: √z = e^(1/2 * ln(z)). This relationship extends the connection between exponentials and roots from real to complex numbers.

How do you find the square root of a complex number in rectangular form?

For z = a + bi, use the formula: √z = ±(√((a + √(a² + b²))/2) + i * sign(b) * √((√(a² + b²) - a)/2)). This involves finding the magnitude and then splitting it between real and imaginary parts.

What is the importance of the complex plane in understanding square roots of complex numbers?

The complex plane provides a geometric interpretation of complex numbers and their operations. For square roots, it helps visualize the two roots as points equidistant from the origin, with arguments related to the original number's argument.

How does the concept of holomorphic functions relate to square roots of complex numbers?

The square root function is holomorphic (complex differentiable) everywhere except along its branch cut. This property is crucial in complex analysis and affects how we define and work with complex square roots.

What is the significance of the unit circle in understanding square roots of complex numbers?

The unit circle in the complex plane is particularly important for understanding roots of unity, including square roots. The square roots of any point on the unit circle lie on the angle bisectors of that point and the positive real axis.

How do square roots of complex numbers relate to the concept of conformal mapping?

The square root function is a conformal map, meaning it preserves angles locally. However, it's not one-to-one on the entire complex plane, which is why we need branch cuts to define a single-valued function.

What is the relationship between square roots and the complex exponential function?

The square root of a complex number z can be expressed using the complex exponential function as √z = |z|^(1/2) * e^(i*arg(z)/2), where arg(z) is the argument of z.

How do you interpret the square root of zero in the complex plane?

The square root of zero is uniquely zero in both the real and complex domains. It's the only complex number with just one square root, as 0² = 0 regardless of which root you choose.

How do square roots of complex numbers relate to the concept of fractional exponents?

Square roots can be seen as a special case of fractional exponents, where the exponent is 1/2. The properties of fractional exponents in complex numbers, including multi-valuedness, apply to square roots.

What is the significance of the complex logarithm in defining square roots of complex numbers?

The complex logarithm allows us to define square roots as z^(1/2) = e^((1/2)ln(z)). However, the multi-valued nature of the complex logarithm leads to the multi-valued nature of complex square roots.

What is the relationship between square roots of complex numbers and the concept of monodromy?

Monodromy describes how a function behaves when following a closed path around a singularity. For square roots, following a path around the origin results in a change of sign, which is a key aspect of its multi-valued nature.

Square root of complex numbers

Maths
Complex Numbers and Quadratic equations
Square root of complex numbers

Square root of complex numbers

Komal MiglaniUpdated on 02 Jul 2025, 07:45 PM IST

The square root of complex numbers is similar to the square root of real numbers but the procedure to find square root is different from real numbers. Just like real numbers, finding the square root of a complex number involves identifying a number that, when squared, returns the original complex number. This requires understanding both the algebraic and geometric representations of complex numbers.

This Story also Contains

Complex Number
What is the Square Root of a Complex Number?
Square Root of Complex Number in Polar Form
Solved Examples Based on Square Root of Complex Numbers

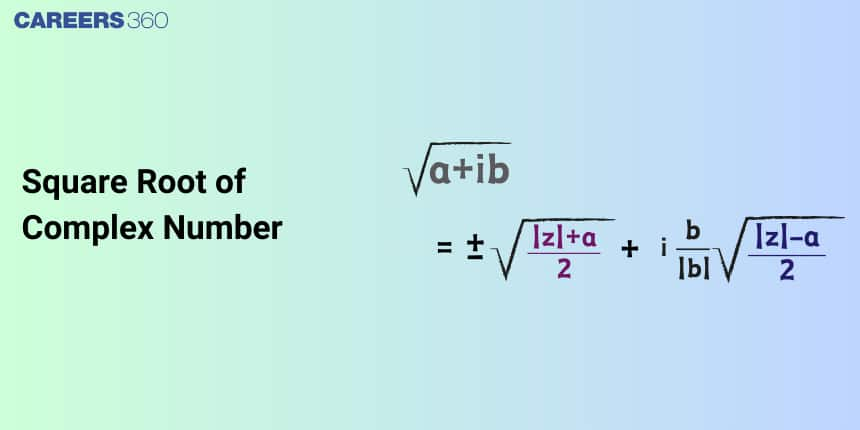
Square root of complex numbers

In this article, we will cover the concept of the square root of complex numbers. This concept falls under the broader category of complex numbers and quadratic equations, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of three questions have been asked on this concept, including two in 2017, and one in 2020.

Complex Number

The number which has no real meaning then these numbers are represented in complex forms. The general form of complex numbers are $a+i b$ where i is iota or$\sqrt{-1}$.

A number of the form $a+i b$ is called a complex number (where a and b are real numbers and i is iota). We usually denote a complex number by the letter $z, z_1, z_2$, etc

For example, $z=5+2 i$ is a complex number.

5 here is called the real part and is denoted by $\operatorname{Re}(z)$ , and 2 is called the imaginary part and is denoted by $\operatorname{Im}(z)$

What is the Square Root of a Complex Number?

A complex number's square root is equal to another complex number whose square equals the original complex number. For example, if $\sqrt{ }(a+i b)=x+i y$ is the square root of the complex number $a+i b$, then $(x+i y) 2=a+i b$. Finding the values of x and y by squaring both sides of the equation $\sqrt{ }(a+i b)=x+i y$ and comparing the real and imaginary parts is one easy method to obtain the square root of a complex integer, a + ib. Let's look at the formula for calculating a complex number's square root.

How to find the square root of complex numbers?

Let $z=x+i y$, is the complex number whose square root we have to find

Since the square root of a complex number must be a complex number,

so let $z^{1 / 2}=a+i b$

Now squaring both sides

$z=x+i y=(a+i b)^2=a^2-b^2+2 i a b$

Now compare real and imaginary parts and find the value of $a$ and $b$ in terms of $x$ and $y$
$
\begin{aligned}
& a^2-b^2=x \\
& 2 a b=y \\
& a^2+b^2=\sqrt{\left(a^2-b^2\right)^2+4 a^2 b^2}=\sqrt{x^2+y^2}=|z|
\end{aligned}
$
By solving (i) and (iii) we get

$
2 a^2=x+|z| \Rightarrow a= \pm \sqrt{\frac{x+|z|}{2}}
$
Similarly we find $b= \pm \sqrt{\frac{|z|-x}{2}}$
So $\sqrt{\mathrm{z}}= \pm\left(\sqrt{\frac{|z|+\operatorname{Re}(\mathrm{z})}{2}}+\mathrm{i} \sqrt{\frac{|\mathrm{z}|-\operatorname{Re}(\mathrm{z})}{2}}\right)$

if Im(z) > 0 otherwise there will be a -ve sign between the real and imaginary parts of the square root of z.

Square Root of Complex Number in Polar Form

The $n^{th}$ root theorem for complex numbers is used to find the square root of a complex number in polar form. According to the nth Root Theorem, if a complex number $z=r(\cos \theta+i \sin \theta)$ is known, then $z_1 / n=$ $\mathrm{r_1}/ \mathrm{n}[\cos [(\theta+2 \mathrm{k} \pi) / \mathrm{n}]+\mathrm{i} \sin [(\theta+2 \mathrm{k} \pi) / n]]$, where $\mathrm{k}=0,1,2,3, \ldots, n-1$, represents the nth root. We add $2 \mathrm{k} \pi$ to $\theta$ to get the complex number's periodic roots. Therefore, we can get the formula to find the square root of a complex number in polar form using the nth root formula. The equation is $Z_1 / 2$ is equal to $r_1 / 2[i \sin [(\theta+2 k \pi) / 2]+\cos [(\theta+2 k \pi) / 2]$ in which $k=0,1$

Note:

1. Students do not need to remember this formula. However, they are required to know the procedure to find the square root of a complex number.

2. If $a+i b$ is one of the square roots of $z$, then the other square root must be $-(a+i b)$

Solved Examples Based on Square Root of Complex Numbers

Example 1: If $(x+i y)^2=7+24 i$ then a value of $(7+\sqrt{-576})^{1 / 2}-(7-\sqrt{-576})^{1 / 2}$ is:

Solution:

As we learned in

Square Root of a Complex Number -
$
\sqrt{z}=a+i b \text { where } z=x+i y
$

is calculated by equating real and imaginary parts of $x+i y=(a+i b)^2$

We have to find $(7+24 i)^{1 / 2}-(7-24 i)^{1 / 2}$

Now $(x+i y)^2=7+24 i$

$x+i y=\sqrt{7+24 i}$

and $x-i y=\sqrt{7-24 i}$ (Put - i at the place of i)

$\therefore \quad i 2 y=\sqrt{7+24 i}-\sqrt{7-24 i}$

Now $x^2-y^2+i 2 x y=7+24$

$\therefore \quad x^2-y^2=7, x y=12$

Solving we get $x= \pm 4 ; y \pm 3$,

$\therefore \quad i 2 y= \pm 6 i$

$\therefore-61$

Hence, the answer is -6i.

Example 2: The region represented by $\{z=x+i y \in C:|z|-\operatorname{Re}(z) \leq 1\}$ is also given by

1) $y^2 \geq 2(x+1)$

2) $y^2 \leq 2(x+1 / 2)$

3) $y^2 \leq(x+1 / 2)$

4) $y^2 \geq\left(x^2+1\right)$

Solution

$\begin{aligned} & |z|-\operatorname{Re}(z) \leq 1 \\ & \Rightarrow \sqrt{x^2+y^2}-x \leq 1 \\ & \Rightarrow \sqrt{x^2+y^2} \leq 1+x\end{aligned}$

$\begin{aligned} & \Rightarrow x^2+y^2 \leq 1+x^2+2 x \\ & \Rightarrow y^2 \leq 2(x+1 / 2)\end{aligned}$

Hence, the answer is the option 2.

Example 3: One of the square roots of $21-20 i$ equals.

Solution:

Let a + ib be the square root

So, $(a+i b)^2=21-20 i$

$a^2-b^2+i(2 a b)=21-20 i$

Thus,

$\begin{aligned} & a^2-b^2=21 \text { and } 2 a b=-20 \\ & a^2-b^2=21 \text { and } a h=-10\end{aligned}$

Using the relation $\left(a^2+b^2\right)^2=\left(a^2-b^2\right)^2+4 a^2 b^2$
$
\begin{aligned}
& \left(a^2+b^2\right)^2=21^2+20^2=841 \\
& a^2+b^2=29
\end{aligned}
$

Adding this equation to $\mathrm{a}^2-\mathrm{b}^2=21$, we get

$a^2=25$

$\therefore a=5$ or $a=-5$

Now using ab = -10, when a= 5 then b= -2 and when a =-5, b= 2

$a+i b=5-2 i$ or $-5+2 i$

Hence, the answer is -5+2i.

Example 4: If $(x+i y)^2=7+24 i$then the value of $(7+\sqrt{-576})^{\frac{1}{2}}-(7-\sqrt{-576})^{\frac{1}{2}}$ is

Solution:
$
\begin{aligned}
& (x+i y)^2=x^2-y^2+2 x y i \\
\Rightarrow & 7+24 i=x^2-y^2+2 x y i \\
\Rightarrow & x^2-y^2=7 \text { and } 2 i x y=24 i \\
\Rightarrow & x^2-y^2=7 \text { and } x y=12
\end{aligned}
$

now start taking values of $x$ and $y$

$
\begin{aligned}
& x= \pm 4 \text { and } y= \pm 3 \\
& (x+i y)-(x-i y)=2 i y= \pm 6 i
\end{aligned}
$
Hence, the answer is -6i.

Example 5: If $z=x-i y$ and $z^{\frac{1}{3}}=p+i q$ then $\frac{\left(\frac{x}{p}+\frac{q}{q}\right)}{\left(p^2+q^2\right)}$ is equal to

Solution:

Equality in Complex Numbers -

$z=x+i y \& w=a+i b$ are equal if $x=a \& y=b$

where in

Two complex numbers are equal if real parts as well as imaginary parts are equal.

$p=x-i y \quad$ and $z^{1 / 3}=p+i d$

$\begin{aligned} & \therefore \quad z=(p+i q)^3 \\ & \therefore x-i y=p^3+(i q)^3+3 p \cdot i q(p+i q)=p^3+i^3 q^3+i p^2 q-3 p q^2 \\ & x-i y=\left(p^3-3 p q^2\right)+i\left(3 p^2 q-q^3\right)\end{aligned}$

Compare: $p^3-3 p q^2=x$

$p\left(p^2-3 q^2\right)=x$

$p^2-3 q^2=\frac{x}{p}$

and $q\left(3 p^2-q^2\right)=-y$

$q^2-3 p^2=\frac{y}{q}$

$\therefore \frac{\frac{x}{p}+\frac{y}{q}}{p^2+q^2}=\frac{p^2-3 q^2+q^2-3 p^2}{\left(p^2+q^2\right)}=\frac{-2\left(p^2+q^2\right)}{p^2+q^2}=-2$

Hence, the answer is -1.

Frequently Asked Questions (FAQs)

Q: How does the concept of harmonic conjugates relate to square roots of complex numbers?

The real and imaginary parts of the complex square root function are harmonic conjugates of each other in regions where the function is analytic. This property is a consequence of the Cauchy-Riemann equations and is important in various applications of complex analysis.

Q: What is the significance of Möbius transformations in understanding square roots of complex numbers?

While square roots themselves are not Möbius transformations, Möbius transformations can be used to simplify calculations involving square roots by mapping the complex plane in ways that preserve their properties.

Q: How do square roots of complex numbers relate to the concept of analytic continuation?

Analytic continuation allows us to extend the definition of square root from positive real numbers to the entire complex plane (except for a branch cut). This process reveals the multi-valued nature of the complex square root function.

Q: What is the connection between square roots of complex numbers and the concept of conformal mapping?

The square root function is a conformal map, meaning it preserves angles locally. However, it's not conformal at the origin (its branch point), where angles are halved.

Q: How does the concept of residues in complex analysis relate to square roots of complex numbers?

While the square root function itself doesn't have residues (as it's not meromorphic), the concept of residues is important when integrating functions involving square roots around closed contours in the complex plane.

Q: What is the significance of the Cauchy-Riemann equations in understanding square roots of complex numbers?

The Cauchy-Riemann equations are satisfied by the square root function wherever it's differentiable, which is everywhere except along its branch cut. This confirms that the square root function is analytic in these regions.

Q: How does the concept of analytic functions apply to square roots of complex numbers?

The square root function is analytic everywhere except along its branch cut. This means it can be represented by a convergent power series at every point where it's defined, which is crucial for many applications in complex analysis.

Q: What is the significance of Riemann surfaces in understanding multi-valued functions like square roots?

Riemann surfaces provide a way to visualize multi-valued functions like square roots as single-valued functions on a more complex surface. For square roots, the Riemann surface consists of two sheets connected at a branch point.

Q: How does the concept of winding number relate to square roots of complex numbers?

The winding number is related to how many times a curve encircles the origin. For square roots, a curve with an odd winding number around the origin will result in the negative of the starting value when following the square root function.

Q: What is the connection between square roots of complex numbers and the cis notation?

The cis notation (cos θ + i sin θ) is useful in expressing complex numbers in polar form. For square roots, if z = r * cis(θ), then √z = √r * cis(θ/2).

Articles

BiPC Courses After 12th - Fees, Eligibility, Duration & Top Institutes

Aug 25, 2025

UPTAC Cutoff 2025 Round 3 (Out) - AKTU Opening and Closing Rank

Aug 23, 2025

UPTAC Counselling 2025 (Started): Internal Sliding, Seat Allotment, Choice Filling, Document Verification

Aug 23, 2025

UPTAC Seat Allotment 2025 for Internal Sliding (Out) - Link, Fee, Seat Acceptance, Reporting

Aug 23, 2025