Cube roots of unity
Cube roots of unity are special complex numbers that, when multiplied by themselves three times, give 1. These roots play an important role in solving equations, working with polynomials, and understanding symmetry in mathematics. The cube roots of unity include one real number and two complex numbers, which are evenly spaced on the unit circle in the complex plane. In this article, we will learn about the formula, properties of cube roots of unity in simple and easy-to-understand terms.
This Story also Contains
- What is Cube Root of Unity?
- Cube Roots of Unity Formua
- How To Find Cube Root Of Unity?
- Operations for Cube Roots of Unity
- Cube Roots of Unity in Polar and Exponential Form
- Deriving Cube Roots of Unity by De Moivre's Theorem
- Properties of Cube roots of unity
- List of topics related to the Cube Roots of Unity
- NCERT Resources
- Practice Questions based on the Cube Roots of Unity

What is Cube Root of Unity?
The cube root of unity is represented as $\sqrt[3]{1}$ and it has three roots. The three cube roots of unity are $1, \omega, \omega^2$, which on multiplication answers unity (1). Among the roots of the cube roots of unity, one root is a real root and the other two roots are imaginary roots. The values of the imaginary cube roots of unity are as follows.
- $\omega=(-1+i \sqrt{ 3} ) / 2$
- $\omega^2=(-1-i \sqrt{3 }) / 2$
| Cube Root of Unity Value | Nature of Cube Root |
|---|---|
| $1$ | Real |
| $-\frac{1}{2} + i\frac{\sqrt{3}}{2}$ | Complex |
| $-\frac{1}{2} - i\frac{\sqrt{3}}{2}$ | Complex |
Cube Roots of Unity Formua
The cube roots of unity are the solutions to the equation $z^3 = 1$. These roots play an important role in algebra, complex numbers, and polynomial equations. By solving this equation, we can find the three distinct complex numbers that, when raised to the power of 3, give 1.
Solving $z^3 = 1$
To find the cube roots of unity, we solve the equation:
$z^3 - 1 = 0$
Factoring the equation gives:
$(z - 1)(z^2 + z + 1) = 0$
So the solutions are $z = 1$ and the roots of $z^2 + z + 1 = 0$. Using the quadratic formula:
$z = \frac{-1 \pm \sqrt{1^2 - 4(1)(1)}}{2(1)}$
$z = \frac{-1 \pm \sqrt{-3}}{2}$
$z = \frac{-1 \pm i\sqrt{3}}{2}$
These are the complex cube roots of unity.
The Three Solutions – $1$, $\frac{-1 + i\sqrt{3}}{2}$, $\frac{-1 - i\sqrt{3}}{2}$
Thus, the three cube roots of unity are:
$_1 = 1$
$z_2 = \frac{-1 + i\sqrt{3}}{2}$
$z_3 = \frac{-1 - i\sqrt{3}}{2}$
These solutions form an equilateral triangle on the unit circle in the complex plane and are evenly spaced at angles of $120^\circ$.
Verification of the Cube Roots
We can verify that these roots satisfy $z^3 = 1$:
For $z_1 = 1: 1^3 = 1$
For $z_2 = \frac{-1 + i\sqrt{3}}{2}$, calculate $z_2^3$ and simplify to check that it equals $1$.
For $z_3 = \frac{-1 - i\sqrt{3}}{2}$, similarly compute $z_3^3$ to confirm it equals $1$.
This shows that all three roots are valid solutions and that cube roots of unity are consistent with the properties of complex numbers and powers.
How To Find Cube Root Of Unity?
Let $z$ be the cube root of unity (1)
So, $z^3=1$
$\Rightarrow \mathrm{z}^3-1=0$
$\Rightarrow(z-1)\left(z^2+z+1\right)=0$
$\Rightarrow \mathrm{z}-1=0$ or $\mathrm{z}^2+\mathrm{z}+1=0$
$
\therefore \mathrm{z}=1 \text { or } \mathrm{z}=\frac{-1 \pm \sqrt{(1-4)}}{2}=\frac{-1 \pm \mathrm{i} \sqrt{3}}{2}
$
Therefore, $\mathrm{z}=1, \mathrm{z}=\frac{-1+\mathrm{i} \sqrt{3}}{2}$ and $\mathrm{z}=\frac{-1-\mathrm{i} \sqrt{3}}{2}$
If the second root is represented by $\boldsymbol{\omega}$, then the third root will be represented by $\boldsymbol{\omega}^2$ (we can check that by squaring the second root, we get the third root)
$
\omega=\frac{-1+\mathrm{i} \sqrt{3}}{2}, \omega^2=\frac{-1-\mathrm{i} \sqrt{3}}{2}
$
So, $1, \omega, \omega^2$ are cube roots of unity and $\omega, \omega^2$ are the non-real complex root of unity.
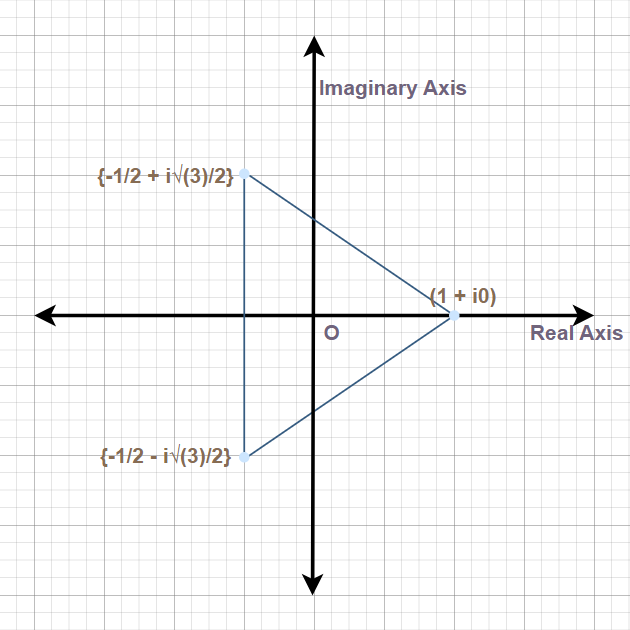
Operations for Cube Roots of Unity
Below are the fundamental operations related to the cube roots of unity, which are the complex numbers satisfying $x^3 = 1$. Understanding these operations is crucial for solving equations and problems involving roots of unity in algebra and complex number theory.
Product of Cube Roots Of Unity
The product of the cube roots of unity is equal to 1. This can be understood from the below expression.
$\begin{aligned} & 1 \times \omega \times \omega^2=1 \times(-1+i \sqrt{ } 3) / 2 \times(-1-i \sqrt{ } 3) / 2 \\ & =\left((-1)^2-(i \sqrt{ } 3)^2\right) /(2 \times 2) \\ & =\left(1-3 i^2\right) / 4 \\ & =(1-3(-1)) / 4 \\ & =4 / 4 \\ & =1 \\ & \therefore 1 \times \omega \times \omega^2=1\end{aligned}$
Sum of Cube Roots of Unity
The sum of the cube roots of unity is equal to zero. This can be observed in the below expression.
$+\omega+\omega^2=1+(-1+i \sqrt{ } 3) / 2+(-1-i \sqrt{ } 3) / 2$
$=1+(-1+i \sqrt{ } 3-1-i \sqrt{ } 3) / 2,=1+(-2 / 2)$
$=1-1=0$
$\therefore 1+\omega+\omega^2=0$
Cube Roots of Unity in Polar and Exponential Form
Cube roots of unity can also be represented in polar form of complex number and exponential notation. Using Euler’s formula, we can express these roots in terms of modulus and argument, making it easier to understand their geometric interpretation and mathematical properties.
Expressing Cube Roots Using Euler’s Formula
Using Euler's form of complex numbers, Euler’s formula states that: $e^{i\theta} = \cos \theta + i\sin \theta$
Using this, the cube roots of unity can be written as:
$z_1 = 1 = e^{i0}$
$z_2 = \frac{-1 + i\sqrt{3}}{2} = e^{i\frac{2\pi}{3}}$
$z_3 = \frac{-1 - i\sqrt{3}}{2} = e^{i\frac{4\pi}{3}}$
These exponential forms simplify calculations involving powers and roots of complex numbers.
Polar Coordinates and Modulus-Argument Form
The polar form of a complex number is given by:
$z = r(\cos \theta + i \sin \theta)$
For the cube roots of unity, all roots lie on the unit circle, so the modulus $r = 1$ and the arguments $\theta$ are:
For $z_1$: $\theta = 0$
For $z_2$: $\theta = \frac{2\pi}{3}$
For $z_3$: $\theta = \frac{4\pi}{3}$
This form shows how the roots are equally spaced around the circle at $120^\circ$ apart.
Connection Between Polar Form and Exponential Notation
The relationship between polar and exponential forms is seamless using Euler’s formula: $z = r e^{i\theta}$
For cube roots of unity, we have:
$z_1 = 1 e^{i 0}$
$z_2 = 1 e^{i \frac{2\pi}{3}}$
$z_3 = 1 e^{i \frac{4\pi}{3}}$
This connection allows us to quickly compute powers and roots, visualize the positions on the complex plane, and apply the formulas in various mathematical and engineering applications.
Deriving Cube Roots of Unity by De Moivre's Theorem
$\sqrt[3]{1}$ can be written as $1^{1 / 3}$. In complex numbers, we have a theorem called De Moivre's Theorem, which is very useful in finding the real and complex roots of a real/complex number. This theorem states:
$
(a+i b)^n=(r(\cos \theta+i \sin \theta))^n=r^n(\cos n \theta+i \sin n \theta), \quad \text { where } n \in \mathbb{Z}
$
Let us assume that $a+i b=1=1+i(0)$. Then we have $a=1$ and $b=0$.
Now,
$
\begin{aligned}
& r=\sqrt{a^2+b^2}=\sqrt{1^2+0^2}=1 \\
& \theta=\tan ^{-1}\left|\frac{b}{a}\right|=\tan ^{-1}\left|\frac{0}{1}\right|=0
\end{aligned}
$
We can write this angle as $0+2 n \pi$, where $n=0,1,2$ (since we need to find three roots, three integer values are taken for $n$ ).
By substituting these values in De Moivre's theorem along with substituting $n=1 / 3$ :
$
\begin{gathered}
(1+i(0))^{1 / 3}=1^{1 / 3}\left(\cos \frac{2 n \pi}{3}+i \sin \frac{2 n \pi}{3}\right), \quad \text { where } n=0,1,2 \\
\Rightarrow 1^{1 / 3}=\cos \frac{2 n \pi}{3}+i \sin \frac{2 n \pi}{3}, \quad \text { where } n=0,1,2
\end{gathered}
$
Finding the Cube Roots
- When $n=0$ :
$
1^{1 / 3}=\cos 0+i \sin 0=1+i(0)=1
$
- When $n=1$ :
$
1^{1 / 3}=\cos \frac{2 \pi}{3}+i \sin \frac{2 \pi}{3}=-\frac{1}{2}+i \frac{\sqrt{3}}{2}=\frac{-1+i \sqrt{3}}{2}(=\omega)
$
- When $n=2$ :
$
1^{1 / 3}=\cos \frac{4 \pi}{3}+i \sin \frac{4 \pi}{3}=-\frac{1}{2}-i \frac{\sqrt{3}}{2}=\frac{-1-i \sqrt{3}}{2}\left(=\omega^2\right)
$
Thus, the cube roots of unity by De Moivre's theorem are:
$
1, \quad \frac{-1+i \sqrt{3}}{2}, \quad \frac{-1-i \sqrt{3}}{2}
$
Properties of Cube roots of unity
i) $1+\omega+\omega^2=0$ and $\omega^3=1$ (Using sum and product of roots relations for the equation $z^3-1=0$ )
ii) To find $\omega^n$, first we write $\omega$ in multiple of 3 with the remainder being 0 or 1 or 2.
Now $\omega^n=\omega^{3 q+r}=\left(\omega^3\right)^q \cdot \omega^r=\omega^r$ (Where r is from $\left.0,1,2\right)$
$
\text { Eg, } \omega^{121}=\omega^{3.40+1}=\left(\omega^3\right)^{40} \cdot \omega^1=\omega
$
iii) $|\omega|=\left|\omega^2\right|=1, \arg (\omega)=2 \pi / 3, \arg \left(\omega^2\right)=4 \pi / 3$ or $-2 \pi / 3$
iv) We can see that $\omega$ and $\omega^2$ differ by the minus sign of the imaginary part hence
v) Cube roots of -1 are $-1,-\omega,-\omega^2$
vi) The cube roots of unity when represented on the complex plane have their point on vertices of a triangle circumscribed by a unit circle whose one vertices lies on the+ve X-axis.

Solved Examples Based On the Cube Root of Unity
Solution:
As we have learned in,
Cube roots of unity -
$
z=(1)^{\frac{1}{3}} \Rightarrow z=\cos \frac{2 k \pi}{3}+i \sin \frac{2 k \pi}{3}
$
$\mathrm{k}=0,1,2$ so z gives three roots
$
\Rightarrow 1, \frac{-1}{2}+i \frac{\sqrt{3}}{2}(\omega), \frac{-1}{2}-i \frac{\sqrt{3}}{2}\left(\omega^2\right)
$
wherein
$
\omega=\frac{-1}{2}+\frac{i \sqrt{3}}{2} \cdot \omega^2=\frac{-1}{2}-\frac{i \sqrt{3}}{2}, \omega^3=1.1+\omega+\omega^2=0
$
1. $\omega . \omega^2$ are cube roots of unity.
given is $\rightarrow w^{100}+\left(w^3\right)^{200}=w^{100}+w^{400}$
$=\left(w^3\right)^{33} \cdot\left(w^3\right)^{153} \cdot w^{15}=2 w=-1+i \sqrt{3}$
Hence, the answer is $-1+i \sqrt{3}$
Example 2: If $\alpha$ and $\beta$ are the roots of the equation $x^2-x+1=0$ then $\alpha^{2009}+\beta^{2009}=$
Solution:
As we have learned
Roots of Quadratic Equation -
$\alpha=\frac{-b+\sqrt{b^2-4 a c}}{2 a}$
$\beta=\frac{-b-\sqrt{b^2-4 a c}}{2 a}$
- wherein
$a x^2+b x+c=0$
is the equation
$a, b, c \in R, \quad a \neq 0$
Cube roots of unity -
$z=(1)^{\frac{1}{3}} \Rightarrow z=\cos \frac{2 k \pi}{3}+i \sin \frac{2 k \pi}{3}$
$k=0,1,2$ so $z$ gives three roots
$\Rightarrow 1, \frac{-1}{2}+i \frac{\sqrt{3}}{2}(\omega), \frac{-1}{2}-i \frac{\sqrt{3}}{2}\left(\omega^2\right)$
- wherein
$
\omega=\frac{-1}{2}+\frac{i \sqrt{3}}{2} \cdot \omega^2=\frac{-1}{2}-\frac{i \sqrt{3}}{2} \cdot \omega^3=1.1+\omega+\omega^2=0
$
1. $\omega, \omega^2$ are cube roots of unity.
$
\alpha, \beta=\frac{1 \pm \sqrt{-3}}{2}=\frac{1 \pm \sqrt{3 i}}{2}=-\left(\frac{-1 \pm \sqrt{3 i}}{2}\right)=-\omega,-\omega^2
$
$\alpha^{2009}+\beta^{200}$
$5^{20 n}+\left(-w^2\right)^{200}$
$
=-\omega^2-\omega=-\left(\omega^2+\omega\right)=-(-1)=1
$
Hence, the answer is 1.
Example 3: Let $\omega$ be a complex number such that $2 w+1=z$ where $z=\sqrt{-3}$ if $\left|\begin{array}{rrr}1 & 1 & 1 \\ 1 & -\omega^2-1 & \omega^2 \\ 1 & \omega^2 & \omega^7\end{array}\right|=3 \mathrm{k}$, then k is equal to :
Solution:
$2 \mathrm{w}+1=\mathrm{z}$
$2 \mathrm{w}+1=\sqrt{3} \mathrm{i}$
$\mathrm{w}=\frac{-1+\sqrt{3} \mathrm{i}}{2}$
$\Rightarrow \mathrm{w}^2=\frac{-1-\sqrt{3} \mathrm{i}}{2}=-\mathrm{w}-1$
$\text { Now, }\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & -\omega^2-1 & \omega^2 \\ 1 & \omega^2 & \omega^7\end{array}\right|=3 k \ldots \ldots$
Given $\Rightarrow\left|\begin{array}{ccc}1 & 1 & 1 \\ 1 & w & w^2 \\ 1 & w^2 & w\end{array}\right|=3 k$
$1\left(w^2-w^4\right)-1\left(w-w^2\right)+1\left(w^2-w\right)=3 k$
$3 w^2-3 w=3 k$
$3\left(w^2-w\right)=3 k$
$k=w^2-w$
$k=-1-2 w$
$=-1-(-1+\sqrt{3} i)$
$=-\sqrt{3} i =-z$
1) $R(z)<0$ and $I(z)>0$
2) $R(z)>0$ and $I(z)>0$
3) $R(z)=-3$
4) $I(z)=0$
Solution:
$\begin{aligned} & z=\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5+\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^3 \\ & z=\left(e^{i \frac{\pi}{6}}\right)^5+\left(e^{-i \frac{\pi}{4}}\right)^3 \\ & =\cos \frac{5 \pi}{6}+i \sin \frac{5 \pi}{6}+\cos \frac{5 \pi}{6}-i \sin \frac{5 \pi}{6} \\ & =2 \cos \frac{5 \pi}{6}<0 \\ & \operatorname{Im}(z)=0\end{aligned}$
Hence, the answer is the option (4).
Solution:
$1+\mathrm{x}^2+\mathrm{x}^4=0$
$\text { Let } \mathrm{x}^2=\mathrm{t}$
$\Rightarrow \mathrm{t}^2+\mathrm{t}+1=0$
$\Rightarrow \mathrm{t}=\omega \text { or } \omega^2$
$\Rightarrow \mathrm{x}^2=\omega \text { or } \omega^2$
$\Rightarrow \alpha^2=\omega \text { or } \omega^2$
$\therefore \alpha^{1011}+\alpha^{2022}-\alpha^{3033}$
$=\alpha\left(\alpha^2\right)^{505}+\left(\alpha^2\right)^{1011}-\alpha\left(\alpha^2\right)^{1516} \ldots(\mathrm{i})$
$=\alpha \cdot \omega^{505}+\omega^{1011}-\alpha \cdot \omega^{1516}$
$=\alpha \omega+1-\alpha \omega = 1$
We get the same answer by putting $\alpha^2=\omega^2$ in (i)
List of topics related to the Cube Roots of Unity
The cube roots of unity are fundamental in understanding complex numbers and their properties, especially in relation to powers and polynomial equations. Below is the list of topics related to the Cube Roots of Unity that are essential for understanding its applications and concepts.
NCERT Resources
This section provides NCERT solutions, exemplar problems, and notes for Class 11 Maths Chapter 5 on Complex Numbers and Quadratic Equations. These resources aid in concept clarity and effective exam preparation.
NCERT Solutions for Class 11 Maths Chapter 5 -Complex Numbers and Quadratic Equations
NCERT Exemplar Class 11 Maths Solutions for Chapter 5 - Complex Numbers and Quadratic Equations
NCERT Class 11 Maths Notes for Chapter 5 - Complex Numbers and Quadratic Equations
Practice Questions based on the Cube Roots of Unity
This section provides practice questions based on the Cube Roots of Unity to enhance conceptual clarity and improve application skills. These problems are useful for revision and effective exam preparation.
Cube Roots Of Unity - Practice Question MCQ
We have shared practice question sets for related topics below: