The chapter on Complex Numbers and Quadratic Equations builds a strong foundation for advanced topics in mathematics and science. Understanding definitions, formulas, and the nature of roots helps in solving a wide range of problems accurately. With regular practice and clear conceptual learning, students can confidently tackle questions in board exams and competitive examinations.
Complex Numbers and Quadratic Equations - Topics, Books, Preparation Tips FAQs
Have you ever wondered what happens when a quadratic equation has no real solution, or how, in mathematics, the square root of a negative number is calculated? These questions lead us to the interesting concepts of complex numbers and quadratic equations, which form an important part of Class 11 Mathematics. In this chapter, a complex number is defined as a number of the form $a+ib$, where $a$ and $b$ are real numbers and $i=\sqrt{-1}$. Quadratic equations, on the other hand, are equations of the form $ax^2+bx+c=0$, which may have real or imaginary roots. Together, these concepts help explain situations where real numbers alone are not sufficient.
This Story also Contains
- Complex Numbers And Quadratic Equations in Mathematics
- Quadratic Equations
- Quadratic Equation Solver
- Complex Numbers and Quadratic Equations in Mathematics: Solved Previous Year Questions
- List of Topics related to Complex Numbers according to NCERT/JEE Mains
- NCERT Resources for Complex Numbers and Quadratic Equations
- Complex Numbers and Quadratic Equations in Different Exams
- Recommended Books for Complex Numbers and Quadratic Equations
- NCERT Subject-wise Resources
- Practice Questions based on Complex Numbers and Quadratic Equations
- Conclusion
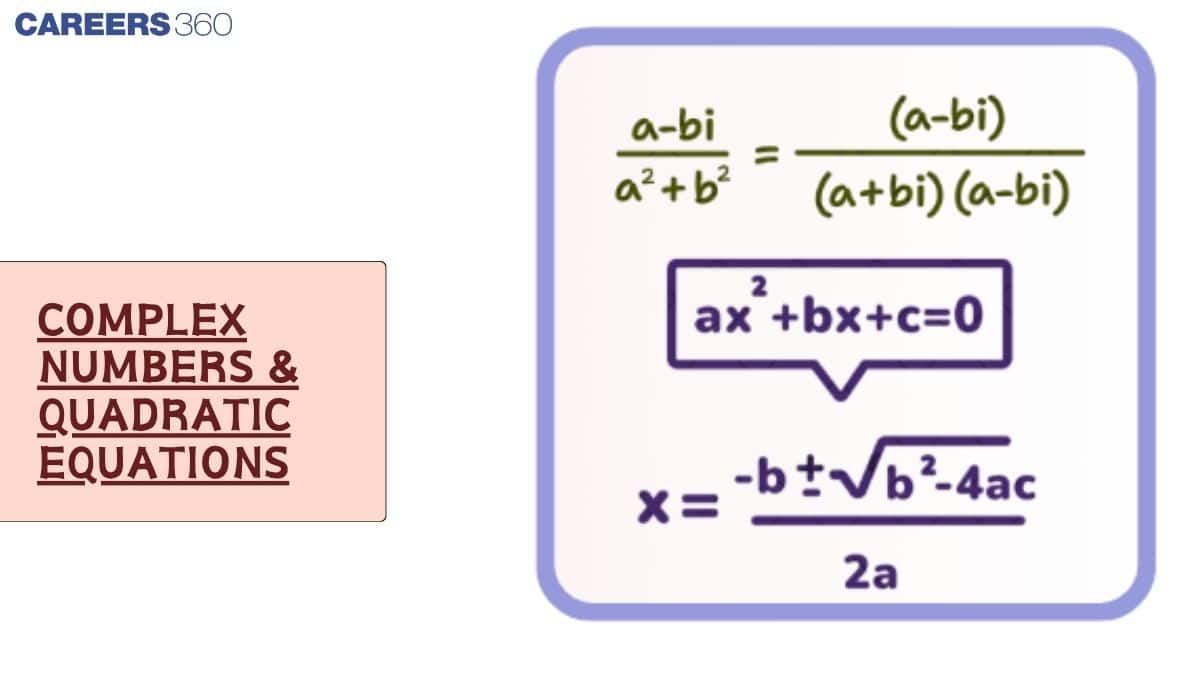
Complex numbers and quadratic equations have many real-life applications. They are widely used in electrical engineering, signal processing, physics, and control systems. For example, complex numbers help analyse alternating current (AC) circuits, while quadratic equations are used to model projectile motion and calculate maximum heights or distances. In this article, you will find Class 11 Complex Numbers and Quadratic Equations notes, including clear definitions, important formulas, methods to determine the nature of roots, solved examples, and practice questions. These explanations are designed to build strong conceptual understanding in Maths and help you prepare confidently for NCERT exams, JEE Mains, and school-level tests.
Complex Numbers And Quadratic Equations in Mathematics
Complex Numbers and Quadratic Equations extend the number system beyond real numbers and help in solving equations with no real solutions. This chapter plays a crucial role in higher mathematics and has important applications in physics, engineering, and competitive exams.
Complex Numbers: Definition
A complex number is a number that can be expressed in the form $x + iy$, where $x$ and $y$ are real numbers and $i$ is the imaginary unit, also called iota. Complex numbers are used to represent quantities that cannot be expressed on the real number line alone.
Example:
$z = 5 + 2i$
-
Real part: $\operatorname{Re}(z) = 5$
-
Imaginary part: $\operatorname{Im}(z) = 2$
The imaginary unit $i$ (iota) is defined as:
$i = \sqrt{-1}$
Powers of $i$
The first few powers of $i$ are important for calculations:
$i^2 = -1$
$i^3 = -i$
$i^4 = 1$
Special Cases
-
Purely real number: If $\operatorname{Im}(z) = 0$, the complex number becomes a real number.
Example: $2 + 0i = 2$ -
Purely imaginary number: If $\operatorname{Re}(z) = 0$, the complex number becomes purely imaginary.
Example: $0 + 2i = 2i$
JEE Main Highest Scoring Chapters & Topics
Focus on high-weightage topics with this eBook and prepare smarter. Gain accuracy, speed, and a better chance at scoring higher.
Download E-bookQuadratic Equations: Definition
The highest power of the variable in a polynomial expression is called the degree of the polynomial.
A polynomial equation in which the highest degree of a variable term is $2$ is called a quadratic equation.
The standard form of a quadratic equation is: $a x^2 + b x + c = 0, \quad a \neq 0$
Here, $a$, $b$, and $c$ are constants (they may be real or complex) and are called the coefficients of the equation. $a$ is also called the leading coefficient.
Examples: $-5x^2 - 3x + 2 = 0$
$x^2 = 0$
$(1+i)x^2 - 3x + 2i = 0$
Since the degree of a quadratic polynomial is $2$, it always has 2 roots (number of real roots + number of imaginary roots = $2$).
Roots of Quadratic Equations
If $f(x)$ is a polynomial, then the equation $f(x) = 0$ is called a polynomial equation.
The roots of the polynomial equation are the values of $x$ for which $f(x) = 0$.
If $x = \alpha$ is a root of $f(x) = 0$, then:
$f(\alpha) = 0$
Example: For $x^2 - 3x + 2 = 0$, $x = 2$ is a root because: $f(2) = 2^2 - 3(2) + 2 = 4 - 6 + 2 = 0$
A polynomial of degree $n$ has $n$ roots (real or complex). Therefore, a quadratic equation always has exactly $2$ roots.
Complex Numbers Formulae
This section covers the essential formulae related to complex numbers, including conjugates, modulus, square roots, and algebraic operations. Understanding these formulae helps simplify calculations and solve problems involving complex numbers efficiently.
Conjugate of Complex Numbers
The conjugate of a complex number $z$ is represented by $\bar{z}$. The pair $(z, \bar{z})$ is called a complex-conjugate pair.
If $z = a + ib$ (where $a, b$ are real numbers), the conjugate is: $ \bar{z} = a - ib $
Conjugates are obtained by changing the sign of the imaginary part, while the real part remains unchanged.
Modulus of a Complex Number
For $z = x + iy$, the modulus of the complex number $z$, denoted by $|z|$, is the distance from the origin in the Argand plane: $|z| = \sqrt{x^2 + y^2}$
It is always a non-negative real number.
Every complex number can be represented as a point in the Argand plane with the $x$-axis as the real axis and the $y$-axis as the imaginary axis: $|z| = \sqrt{x^2 + y^2} = r$ where $r$ is the distance from the origin to the point $(x, y)$.
Square Root of a Complex Number
If $z = a + ib$, the square root of the complex number $z$ is another complex number whose square equals $z$. If $\sqrt{z} = x + iy$, then: $(x + iy)^2 = a + ib$
The formula to find the square root is: $\sqrt{z} = \pm \left( \sqrt{\frac{|z| + \operatorname{Re}(z)}{2}} + i \sqrt{\frac{|z| - \operatorname{Re}(z)}{2}} \right)$
If $\operatorname{Im}(z) < 0$, the sign of the imaginary part is negative.
Algebraic Operations on Complex Numbers
This section explains the fundamental algebraic operations on complex numbers, including addition, subtraction, multiplication, and division.
Addition
Let $z_1 = a + ib$ and $z_2 = c + id$, then: $z_1 + z_2 = (a + c) + i(b + d)$
Example: $(2 + 3i) + (2 + 2i) = (2 + 2) + i(3 + 2) = 4 + 5i$
Subtraction
Let $z_1 = a + ib$ and $z_2 = c + id$, then: $z_1 - z_2 = (a - c) + i(b - d)$
Example: $(6 + 10i) - (10 + 3i) = (6 - 10) + i(10 - 3) = -4 + 7i$
Multiplication
Let $z_1 = a + ib$ and $z_2 = c + id$, then: $(a + ib)(c + id) = (ac - bd) + i(ad + bc)$
Example: $2i(2 + 6i) = (0 + 2i)(2 + 6i) = 0 + 12i^2 + 4i = -12 + 2i$
Division
Let $z_1 = c_1 + id_1$ and $z_2 = c_2 + id_2$, then the quotient is:
$\frac{z_1}{z_2} = z_1 \cdot \frac{1}{z_2}$
To divide, multiply $z_1$ by the reciprocal of $z_2$:
$\frac{z_1}{z_2} = z_1 \cdot \frac{\bar{z_2}}{|z_2|^2}$
Quadratic Equations
Solving quadratic equations means finding the value(s) of the variable that satisfy the equation. These values are called roots, solutions, or zeros. Since the degree of a quadratic equation is $2$, it can have a maximum of $2$ roots.
Example: For the equation $x^2 - 3x + 2 = 0$, we can see that $x = 1$ and $x = 2$ satisfy the equation, so these are its roots. But how do we find roots if they are not obvious?
There are several methods to solve quadratic equations:
-
Solving by factoring
-
Solving by completing the square
-
Solving by graphing
-
Solving using the quadratic formula
Nature of Roots
The nature of the roots of a quadratic equation depends on the discriminant $D = b^2 - 4ac$.
-
Real and Distinct Roots
-
$D > 0$
-
The curve intersects the $x$-axis at two distinct points.
-
-
Real and Equal Roots
-
$D = 0$
-
The curve intersects the $x$-axis at only one point.
-
-
Complex Roots
-
$D < 0$
-
The curve does not intersect the $x$-axis.
-
How to Find the Nature of Roots
Step 1: Compare the given quadratic equation with the standard form $ax^2 + bx + c = 0$ to find the coefficients $a$, $b$, and $c$.
Step 2: Substitute the coefficients into the discriminant: $D = b^2 - 4ac$ and solve.
Step 3: Determine the nature of the roots based on $D$:
-
If $D < 0$, the roots are complex
-
If $D = 0$, the roots are real and equal
-
If $D > 0$, the roots are real and distinct
| $b^2-4 a c$ $> 0$ | Real and unequal |
| $b^2-4 a c$ $= 0$ | Real and equal |
| $b^2-4 a c$ $< 0$ | Unequal and Imaginary |
| $b^2-4 a c$ $> 0$ (is a perfect square) | Real, rational and unequal |
| $b^2-4 a c$ $> 0$ (is not a perfect square) | Real, irrational and unequal |
| $b^2-4 a c$ $> 0$ (is aperfect square and $a$ or $b$ is irrational) | Irrational |
Sum and Product of Roots of a Quadratic Equation
Assume $\alpha$ and $\beta$ are the roots of a quadratic equation $ax^2 + bx + c = 0$.
Sum of Roots:
$\alpha + \beta = \frac{-b + \sqrt{D}}{2a} + \frac{-b - \sqrt{D}}{2a} $
$= \frac{-b}{2a} + \frac{\sqrt{D}}{2a} + \frac{-b}{2a} - \frac{\sqrt{D}}{2a} $
$= \frac{-2b}{2a} $
$= \frac{-b}{a} $
Product of roots:
$\alpha \cdot \beta = \frac{(-b + \sqrt{D})}{2a} \cdot \frac{(-b - \sqrt{D})}{2a} $
$= \frac{(-b)^2 - (\sqrt{D})^2}{(2a)^2} $
$= \frac{b^2 - D}{4a^2} $
$= \frac{b^2 - b^2 + 4ac}{4a^2} \quad [D = b^2 - 4ac] $
$= \frac{c}{a} $
A quadratic equation can be formed using the sum and product of roots:
$x^2 - (\alpha + \beta)x + (\alpha \cdot \beta) = 0 $
Location of Roots
Now, let us look into the location of the roots of quadratic equations.
Let $f(x) = ax^2 + bx + c$ where $a, b, c$ are real numbers and $a \neq 0$. Let $x_1$ and $x_2$ be the roots of $f(x)$ and let $k$ be any real number.
1. If both roots of $f(x)$ are less than $k$:
i) $D \ge 0$ (the roots may be distinct or equal)
ii) $a f(k) > 0$ (in both cases, $a f(k)$ is positive; if $a < 0$, then $f(k) < 0$, and multiplying two negative values gives a positive value)
iii) $k > -\frac{b}{2a}$ (since $-\frac{b}{2a}$ lies between $x_1$ and $x_2$, and $x_1, x_2 < k$, so $-\frac{b}{2a} < k$)
2. If both roots of $f(x)$ are greater than $k$:
i) $D \ge 0$
ii) $a f(k) > 0$
iii) $k < -\frac{b}{2a}$ (since $-\frac{b}{2a}$ lies between $x_1$ and $x_2$, and $x_1, x_2 > k$, so $-\frac{b}{2a} > k$)
Condition for a number $k$ with respect to the roots:
-
Let $f(x) = ax^2 + bx + c$ with real coefficients and $a \neq 0$.
-
Let $x_1$ and $x_2$ be the real roots of the quadratic equation.
Case (i): $k$ lies between the roots $x_1$ and $x_2$
i) $D \ge 0$
ii) $k_1 < -\frac{b}{2a} < k_2$, where $k_1 < k_2$
Case (ii): $k_1$ and $k_2$ lie between the roots
i) $a f(k_1) < 0$ and $a f(k_2) < 0$
Quadratic Equation Solver
Students can use the following link to solve and find the roots of quadratic equations in the form $ax^2+bx+c=0$. Values up to 12 can be checked there. Students can also plot the graph of the quadratic function and examine it at up to four different points. Additionally, the calculator displays key properties such as the discriminant, vertex coordinates, and the sum and product of roots, helping you understand how each coefficient affects the shape and position of the parabola.
Complex Numbers and Quadratic Equations in Mathematics: Solved Previous Year Questions
Solution:
As we have learned
Polar Form of a Complex Number -
$z=r(\cos \theta+i \sin \theta)$
- wherein
$\mathrm{z}=$ modulus of z and $\theta$ is the argument of Z
Euler's Form of a Complex Number -
$z=r e^{i \theta}$
- wherein
r denotes the modulus of z, and $\theta$ denotes the argument of z.
$z=x+i y=r(\cos \theta+i \sin \theta)$
$=r e^{i \theta}$
So, $\operatorname{Im} z^5=\operatorname{Im}\left(r e^{i \theta}\right)^5$
$=\operatorname{Im}\left(r^5 e^{i \theta 5}\right)$
$=r^5 \sin 50$
$(\operatorname{Im} z)^5=(r \sin \theta)^5$
$=\left(r^5 \sin ^5 \theta\right)$
So, $\frac{\operatorname{Im} z^5}{(\operatorname{Im} z)^5}=\frac{\sin 5 \theta}{\sin ^5 \theta}$
for minimum value, differentiating w.r.t $\theta$
So, $\frac{\sin ^5 \theta \cdot 5 \cos \theta-5 \sin 5 \theta \sin ^4 \theta \cos \theta}{\sin ^{10} \theta}$
$\Rightarrow \sin \theta \cdot \cos 5 \theta-\sin 5 \theta \cos \theta=0$
$
\begin{aligned}
& \Rightarrow \sin 4 \theta \cdot=0 \\
& 4 \theta=n \pi \\
& \theta=n \pi / 4
\end{aligned}
$
for $\mathrm{n}=1$
$\frac{\sin 5 \theta}{\sin ^5 \theta}=\frac{-1 / \sqrt{2}}{(1 / \sqrt{2})^5}=-4$
Hence, the answer is -4.
Solution:
Definition of Argument/Amplitude of z in Complex Numbers -
$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$
$\theta, \pi-\theta,-\pi+\theta,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant, respectively.
$z=(1)^{\frac{1}{3}} \Rightarrow z=\cos \frac{2 k \pi}{3}+i \sin \frac{2 k \pi}{3}$
k=0,1,2, so z gives three roots
$\Rightarrow 1, \frac{-1}{2}+i \frac{\sqrt{3}}{2}(\omega), \frac{-1}{2}-i \frac{\sqrt{3}}{2}\left(\omega^2\right)$
- wherein
$\omega=\frac{-1}{2}+\frac{i \sqrt{3}}{2}, \omega^2=\frac{-1}{2}-\frac{i \sqrt{3}}{2}, \omega^3=1,1+\omega+\omega^2=0$
$1, \omega, \omega^2$ are cube roots of unity.
$x^2+x+1=0$, roots are, $\omega$ and $\omega^2$ where $\omega$ is the cube root of unity.
$
z=3+6 i\left(z_0\right)^{81}-3 i\left(z_0\right)^{90}
$
$z_0=\omega$ and $\omega^2$
$
\begin{aligned}
& z=3+6 i(\omega)^{81}-3 i(\omega)^{93} \\
& z=3+3 i \quad \because \omega^3=1 \\
& \arg (z)=\frac{1}{4}
\end{aligned}
$
Hence, the required answer is $\frac{\pi}{4}$.
Example 3: z is a complex number such that $z+\bar{z}=5$ and $z-\bar{z}=7 i$ then z equals
Solution:
We know the properties of the conjugate of a complex number:
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i}$, where
$\operatorname{Im}(z)$ denotes the imaginary part of $z$
$\bar{z}$ denotes the conjugate of $z$
$z + \bar{z} = 5$
$z - \bar{z} = 7i$
Adding both: $2z = 5 + 7i \Rightarrow z = \frac{5}{2} + \frac{7}{2}i$
Or, using formulas: $\operatorname{Re}(z) = \frac{z + \bar{z}}{2} = \frac{5}{2}$ and $\operatorname{Im}(z) = \frac{z - \bar{z}}{2i} = \frac{7}{2}$
Hence, the answer is $z = \frac{5}{2} + \frac{7}{2}i$
Example 4: z is a complex number such that $z-\bar{z}=4 i$ , then $\operatorname{Im}(z)$ equals
Solution:
As we learned in properties of the conjugate of a complex number:
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i}$ where $\operatorname{Im}(z)$ denotes the imaginary part of $z$
$\bar{z}$ denotes the conjugate of $z$
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i} = \frac{4i}{2i} = 2$
Hence, the answer is $2$.
Example 5: The multiplicative inverse of the complex number $z=\frac{5+i \sqrt{2}}{1-i \sqrt{2}}$ is:
Solution:
As we have learnt, the multiplicative inverse of $z$ is $\frac{1}{z}$
Now, $z = \frac{5+i \sqrt{2}}{1-i \sqrt{2}}$
$\frac{1}{z} = \frac{1-i \sqrt{2}}{5+i \sqrt{2}}$
$= \frac{1-i \sqrt{2}}{5+i \sqrt{2}} \cdot \frac{5-i \sqrt{2}}{5-i \sqrt{2}}$
$= \frac{5-i \sqrt{2}-i 5 \sqrt{2}-2}{25+2}$
$= \frac{3-6 \sqrt{2} i}{27}$
$= \frac{3(1-2 \sqrt{2} i)}{27}$
$= \frac{1-2 \sqrt{2} i}{9}$
So, the multiplicative inverse is $\frac{1-2 i \sqrt{2}}{9}$.
Hence, the answer is option 2.
List of Topics related to Complex Numbers according to NCERT/JEE Mains
This section covers all essential topics on complex numbers as per NCERT and JEE Main syllabus. Understanding these topics thoroughly helps in solving a wide variety of problems in algebra, coordinate geometry, and higher-level mathematics.
NCERT Resources for Complex Numbers and Quadratic Equations
Below are the NCERT Solutions, Exemplar problems, and concise notes for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations. These resources will help in understanding concepts and practising exam-relevant questions.
Complex Numbers and Quadratic Equations in Different Exams
The chapter on Complex Numbers and Quadratic Equations is an important part of Class 11 Mathematics and is frequently tested in school and competitive exams. The table below outlines the exam-wise focus areas, commonly asked topics, and effective preparation strategies to help students plan their studies efficiently.
| Exam Name | Focus Area | Common Topics Asked | Preparation Tips |
|---|---|---|---|
| CBSE Board | Conceptual clarity & numericals | Definition of complex numbers, algebra of complex numbers, quadratic equations, roots | Study the NCERT theory and solve all examples and exercises |
| JEE Main | Problem-solving & accuracy | Modulus and argument, quadratic equations, nature of roots | Practise MCQs and numerical-based problems regularly |
| JEE Advanced | Analytical thinking | Locus problems, properties of complex numbers, and advanced quadratic equations | Solve previous years’ advanced-level questions |
| NEET | Basics & speed | Simple complex number operations, quadratic formulas | Focus on formula application and quick calculations |
| State Board Exams (ICSE, UP Board, RBSE, etc) | Theory-oriented | Definitions, properties, standard forms, simple problems | Revise textbook concepts and practice solved examples |
| Mathematics Olympiads | Concept application | Geometry using complex numbers, advanced root-based problems | Strengthen fundamentals and practise high-level problems |
Recommended Books for Complex Numbers and Quadratic Equations
Here is a list of standard books that provide clear explanations, solved examples, and practice problems on complex numbers and quadratic equations, ideal for NCERT, JEE Mains, and other competitive exams.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Mathematics Textbook (Class 11) | NCERT | Official textbook with clear explanations, foundational concepts, and exercises on complex numbers and quadratic equations. Essential for board exam preparation. |
| Higher Algebra | Hall & Knight | A classic and comprehensive book on algebra, covering complex numbers and quadratic equations thoroughly for a deeper understanding. |
| Algebra for JEE Main & Advanced | Arihant Publications | Includes theory, solved examples, and practice problems focused on complex numbers and quadratics, tailored for JEE aspirants. |
| Complex Numbers and Quadratic Equations | M.L. Khanna | Detailed explanations and practice exercises specific to the topics, with a focus on problem-solving techniques. |
| Problems in Algebra | V.L. Malakhov | Collection of varied difficulty problems on quadratic equations and complex numbers to enhance problem-solving skills. |
NCERT Subject-wise Resources
These NCERT resources cover each subject in a structured manner, offering theory, examples, and exercises that are essential for building a strong foundation in subject-wise key concepts.
| Resource | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT Notes Class 11 Maths | NCERT Notes Class 11 Physics | NCERT Notes Class 11 Chemistry |
| NCERT Solutions | NCERT Solutions for Class 11 Mathematics | NCERT Solutions for Class 11 Physics | NCERT Solutions for Class 11 Chemistry |
Practice Questions based on Complex Numbers and Quadratic Equations
These practice questions help in boosting your understanding of complex numbers, including operations, conjugates, modulus, and quadratic equations, roots, allowing you to apply formulas and solve problems efficiently.
Conclusion
Frequently Asked Questions (FAQs)
Q: What are complex numbers and quadratic equations?
A:
A complex number is a number of the form $x + iy$, where $x$ and $y$ are real and $i = \sqrt{-1}$. A quadratic equation is a polynomial equation of degree 2, written as $ax^2 + bx + c = 0$.
Q: What is a complex number called?
A:
A number of the form $x + iy$ is called a complex number.
Q: What is the root of a quadratic equation?
A:
The root is the value of $x$ that satisfies $ax^2 + bx + c = 0$, also called a solution or zero of the equation.
Q: What is pure imaginary numbers?
A:
If the real part of the complex number is zero, then the complex number becomes a purely imaginary number. Eg. $0+2 i=2 i$
Q: What is the value of iota?
A:
lota is an imaginary unit number that is denoted by $i$ and the value of iota is $\sqrt{-1}$ i.e., $i=\sqrt{-1}$. For analyzing the powers of iota, we calculate the first few powers of iota. i.e $i=\sqrt{-1}, i^2=-1, i^3=-\sqrt{-1}, i^4=1$
Q: What are the 4 four methods of solving quadratic equations?
A:
There are different ways of solving quadratic equations.
- Solving quadratic equations by factoring
- Solving quadratic equations by completing the square
- Solving quadratic equations by graphing
- Solving quadratic equations by quadratic formula
Articles