Mole Concept Basics - Definition, Formula, Examples, FAQs

To define the quantity of any substance in the field of chemistry, we use the term "mole". It is defined as the quantity comprising 6.022 × 10²³ elementary units. They can be atoms, molecules, ions, or electrons. The value mentioned is defined by the name as Avogadro's number, after the famous Italian scientist, Amedeo Avogadro. This number helps chemists calculate entities during a chemical reaction and relate the mass of the substance to the number of particles it contains. For instance, one mole of carbon would weigh 12 grams, which would have 6.022 × 10²³ atoms of carbon.

This Story also Contains

1. Understanding the Mole
2. Relationship of Mole
3. Determining the Total Number of Entities
4. Some Solved Examples
5. Conclusion

Understanding the Mole

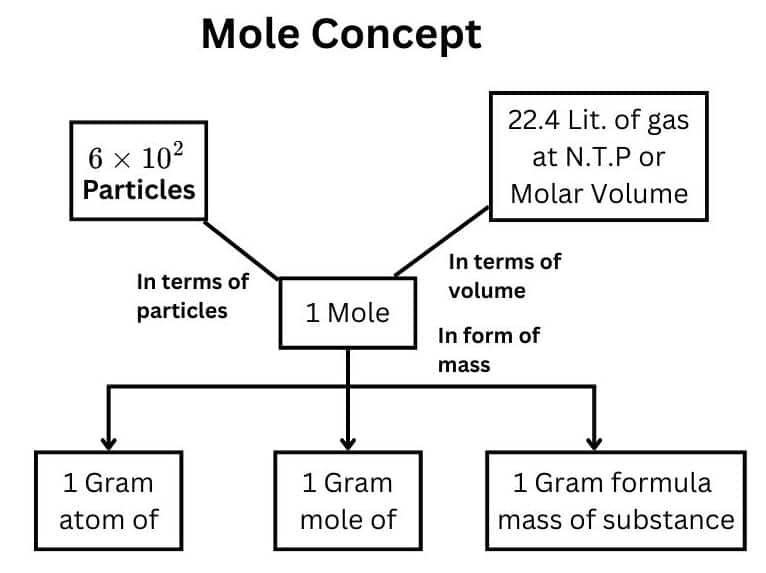
• A mole is a unit that represents 6.023 x 10²³ particles, atoms, molecules ions, etc., irrespective of their nature.
• Mole is related to the mass of the substance, the volume of the gaseous substance, and the number of particles
• $n=\frac{m}{M}$

where m = Wt. of substance in grams. and M = Molar mass of substance in G.m.m.

Here G.m.m = Gram molecular mass or molar mass, which is the mass of 1 mole of any substance

• Mole = (Volume of substance in litre )22.4 litre
• The volume of one mole of any gas is equal to 22.4 liters or dm³ at STP. It is known as molar volume.
• Mole = Number of identities Avogadro's number

Related Topics,

• Example Chemical Change
• Chemical Reactions
• Types of Chemical Reactions
• Physical Change Chemical Change
• Laws of Chemical Combination for Elements and Compounds

Relationship of Mole

A mole of any substance (like O₂) stands for:

• 6.023 x 10²³ molecules of O₂
• 2 x 6.023 x 10²³ atoms of Oxygen
• 32 gm of Oxygen
• 22.4 litre of O₂ at STP.

Determining the Total Number of Entities

1. Total number of molecules = mole(n) x N_A
2. Total number of Atoms = mole (n) x N_A x No. of atoms present in one molecule (atomicity).
3. Total number of Electrons = mole (n) x N_A x No. of electrons present in one atom.
4. The total charge on any ion = mole (n) x N_A x charge on one ion x 1.6 x 10^-19 C

Also read -

Recommended topic video on (Mole Concept Basic )

Some Solved Examples

Que 1: Number of atoms in 558.5 gram Fe (at. wt. of Fe = 55.85 g mol^-1) is:

1) twice that in 60 g carbon

2) 6.023 × 10²²

3) half that in 8 g He

4) 558.5 × 6.023 × 10²³

Solution

Number of moles of Fe atom =558.555.85=10Mole

Total number of atom

=10×6.022×1023=6.022×1024=10×NA

12 g of carbon means Avogadro's number,

therefore, 60 g of carbon means, 5 moles of carbon and thus contains 5×N_A atoms, twice of this equals 10N_A atoms of carbon.

Hence, the answer is the option (1).

Que 2: If we consider that 1/6, in place of 1/12, the mass of the carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

1) decrease twice

2) increase two-fold

3) remain unchanged

4) be a function of the molecular mass of the substance.

Solution

When you consider 1/6 in place of 1/12 since the mass of the carbon atom is still the same, new amu1 = 2amu ( where amu1 is the new amu unit and amu is the old amu unit). So now Na1 (Avogadro's number) becomes half ( Na/2) since the weight of carbon corresponding to atomic weight becomes 6gm in place of 12. ( where Na1 is the new Avogadro's number and Na is the old Avogadro's number). And we know that the mass of one mole of a substance is = Na x amu. So new atomic mass= Na1 x amu1 = Na/2 x 2amu = Na x amu = old atomic weight.

Hence, the answer is the option (3).

Que 3: What is the total number of moles if we have a mixture of 34g of Ammonia, 78g of Benzene, and 10g of Hydrogen?

1) 8

2) 9

3) 7

4) 10

Solution

Number of moles of ammonia = mass of ammonia molar mass of ammonia =3417=2

Number of moles of benzene =7878=1

Number of moles of hydrogen =102=5

Total number of moles = 2 + 1 + 5 = 8

Hence, the answer is (8).

Que 4: We have a substance x. What is the molar mass (in g) of x if 2 moles of it weigh 196g?

1) 147

2) 196

3) 98

4) 49

Solution

Molar mass of x=1962g=98g

Hence, the answer is (98g).

Que 5. 14 g of Nitrogen gas and 22 g of CO₂ gas are mixed together. Find the volume of the gaseous mixture at STP.

(Response should be up to only one decimal digit like 78.7).

1) 22.4

2) 11.2

3) 44.8

4) 52.8

Solution

Number of Moles of a gas at STP -

no. of moles of a gas at STP = given volume of gas / 22.4 liter

Moles of N₂=0.5

moles of CO₂=0.5

So total moles 0.5+0.5=1

So vol. at STP =1×22.4=22.4lit

Hence, the answer is the option (1).

Conclusion

The number 6.022 x 10²³ is called the Avogadro number or Avogadro constant. It is denoted by N_A in honor of nineteenth-century Italian scientist, Amedeo Avogadro. In other words, a mole is an Avogadro number of particles. The mass of one mole of any substance will be its molar mass and it contains 6.022 x 10²³ particles of that substance.

Also, check