Indefinite Integrals - Definition, Properties, Formulas & Examples

Indefinite Integral Formulas

Edited By Komal Miglani | Updated on Jul 02, 2025 08:08 PM IST

Integration of indefinite integral is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These concepts of integration have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

Indefinite Integral Formulas

In this article, we will cover the concept of Integration of indefinite integral. This concept falls under the broader category of Calculus, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of two questions have been asked on this concept, including one in 2014, one in 2018, and one in 2021.

Integration of Indefinite Integral:

Integration is the reverse process of differentiation. In integration, we find the function whose differential coefficient is given. The rate of change of a quantity $y$ concerning another quantity $x$ is called the derivative or differential coefficient of $y$ concerning $x$. Geometrically, the Differentiation of a function at a point represents the slope of the tangent to the graph of the function at that point.

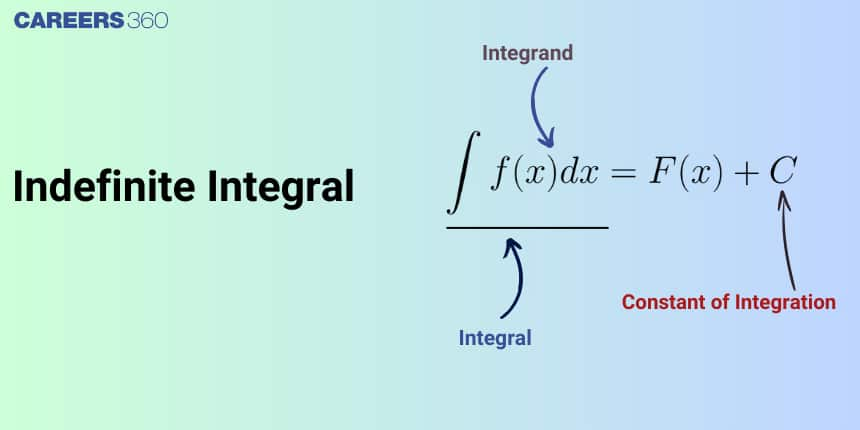
An intergral for which the limits are not defined is called the indefinite integral. An indefinite integral, denoted as $\int f(x) d x$. It is expressed as $\int f(x) d x=F(x)+C$. where $\mathrm{F}(\mathrm{x})$ is any antiderivative of $\mathrm{f}(\mathrm{x})$ and C is the constant of integration.

Fundamental Formulae (Inverse Trigonometric Functions)
1. $\frac{d}{d x}\left(\sin ^{-1} \frac{x}{a}\right)=\frac{1}{\sqrt{a^2-x^2}} \Rightarrow \int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1}\left(\frac{x}{a}\right)+C$
2. $\frac{d}{d x}\left(\cos ^{-1} \frac{x}{a}\right)=\frac{-1}{\sqrt{a^2-x^2}} \Rightarrow \int \frac{-1}{\sqrt{a^2-x^2}} d x=\cos ^{-1}\left(\frac{x}{a}\right)+C$
3. $\frac{d}{d x}\left(\frac{1}{a} \tan ^{-1} \frac{x}{a}\right)=\frac{1}{a^2+x^2} \Rightarrow \int \frac{d x}{a^2+x^2}=\frac{1}{a} \tan ^{-1}\left(\frac{x}{a}\right)+C$
4. $\frac{d}{d x}\left(\frac{1}{a} \cot ^{-1} \frac{x}{a}\right)=\frac{-1}{a^2+x^2} \Rightarrow \int \frac{-1}{a^2+x^2} d x=\frac{1}{a} \cot ^{-1}\left(\frac{x}{a}\right)+C$
5. $\frac{d}{d x}\left(\frac{1}{a} \sec ^{-1} \frac{x}{a}\right)=\frac{1}{x \sqrt{x^2-a^2}} \Rightarrow \int \frac{d x}{x \sqrt{x^2-a^2}}=\frac{1}{a} \sec ^{-1}\left(\frac{x}{a}\right)+C$
6. $\frac{d}{d x}\left(\frac{1}{a} \csc ^{-1} \frac{x}{a}\right)=\frac{-1}{x \sqrt{x^2-a^2}} \Rightarrow \int \frac{-d x}{x \sqrt{x^2-a^2}}=\frac{1}{a} \csc ^{-1}\left(\frac{x}{a}\right)+C$

Basic integration rules,
(i) $\frac{d}{d x}\left(\frac{x^{n+1}}{n+1}\right)=x^n$;
$\int x^n d x=\frac{x^{n+1}}{n+1}+$ C, $n \neq-1$

Particularly, we note that
$\frac{d}{d x}(x)=1$;
$\int d x=x+C$

(ii) $\frac{d}{d x}(\sin x)=\cos x$;
$\int \cos x d x=\sin x+C$

(iii) $\frac{d}{d x}(-\cos x)-\sin x$;
$\int \sin x d x=-\cos x+\mathrm{C}$

(iv) $\frac{d}{d x}(\tan x)-\sec ^2 x$;
$\int \sec ^2 x d x=\tan x+C$

(v) $\frac{d}{d x}(-\cot x)=\operatorname{cosec}^2 x$;
$\int \operatorname{cosec}^2 x d x=-\cot x+C$

(vi) $\frac{d}{d x}(\sec x)=\sec x \tan x$;
$\int \sec x \tan x d x=\sec x+C$

(vii) $\frac{d}{d x}(-\operatorname{cosec} x)=\operatorname{cosec} x \cot x$;
$\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+4$

(viii) $\frac{d}{d x}\left(\sin ^{-1} x\right)-\frac{1}{\sqrt{1-x^2}}$;
$\int \frac{d x}{\sqrt{1-x^2}}=\sin ^{-1} x+C$

(ix) $\frac{d}{d x}\left(-\cos ^{-1} x\right)=\frac{1}{\sqrt{1-x^2}}$;
$\int \frac{d x}{\sqrt{1-x^2}}=-\cos ^{-1} x+C$

(x) $\frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^2}$;
$\int \frac{d x}{1+x^2}=\tan ^{-1} x+C$

(xi) $\frac{d}{d x}\left(-\cot ^{-1} x\right)=\frac{1}{1+x^2} ; \quad \int \frac{d x}{1+x^2}=-\cot ^{-1} x+\mathrm{C}$

Solved Examples based on Indefinite Integral

Example 1: If $\int \frac{2 x+5}{\sqrt{7-6 x-x^2}} d x=A \sqrt{7-6 x-x^2}+B \sin ^{-1}\left(\frac{x+3}{4}\right)+C$ (where C is a constant of integration), then the ordered pair ( A , B ) is equal to :
1) $(2,1)$
2) $(-2,-1)$
3) $(-2,1)$
4) $(2,-1)$

Solution
Integration by perfect square method -

$a x^2+b x+c=a\left[x^2+\frac{b x}{a}+\frac{c}{a}\right]=a\left[\left(x+\frac{b}{2 a}\right)^2+\frac{c}{a}-\frac{b^2}{4 a^2}\right]$

Make the coefficient of $x^2$ +ve one .

and

$\begin{aligned}
& I=\int \frac{2 x+5}{\sqrt{7-6 x-x^2}} d x \\
& =-\int \frac{(-2 x-5)}{\sqrt{7-6 x-x^2}} d x \\
& =-\int \frac{-6-2 x-5+6}{\sqrt{7-6 x-x^2}} d x \\
& =\int\left(-\frac{-2 x-6}{\sqrt{-x^2-6 x+7}}-\frac{1}{\sqrt{-x^2-6 x+7}}\right) \mathrm{d} x \\
& =-2 \sqrt{-x^2-6 x+7}-\int \frac{1}{\sqrt{16-(x+3)^2}} \mathrm{~d} x \\
& =-2 \sqrt{7-6 x-x^2}-\sin ^{-1}\left(\frac{x+3}{4}\right)+C \\
& \mathrm{~A}=-2 ; \mathrm{B}=-1
\end{aligned}$

Hence, the answer is the option 2.

Example 2: If $I_1=\int \frac{d x}{\sqrt{a^2-x^2}}$ and $I_2=\int \cos ^{-1} \frac{x}{a}$ then $I_1+I_2=$ ?

1) $\sin ^{-1} \frac{x}{a}+c$

2) $\cos ^{-1} \frac{x}{a}+c$

3) Constant value

4) None of these

Solution

As we have learnt,

Integrals of inverse circular functions -

$\begin{aligned}
& \frac{\mathrm{d}}{\mathrm{d} x}\left(\sin ^{-1} \frac{x}{a}\right)=\frac{1}{\sqrt{a^2-x^2}} \\
& \therefore \int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+c \\
& I_1=\int \frac{d x}{\sqrt{a^2-x^2}}=\sin ^{-1} \frac{x}{a}+c
\end{aligned}$

Also,

$I_1+I_2=\sin ^{-1} \frac{x}{a}+\cos ^{-1} \frac{x}{a}+c=\frac{\pi}{2}+c=C$

Hence, the answer is the option 3.

Example 3: If the value of the integral $\int_0^{\frac{1}{2}} \xrightarrow[\left(1-x^2\right)^{\frac{3}{2}}]{x^2} d x$ is $\frac{k}{6}$ then $k$ is equal to?
1) $2 \sqrt{3}-\pi$
2) $2 \sqrt{3}+\pi$
3) $3 \sqrt{2}+\pi$
4) $3 \sqrt{2}-\pi$

Solution

$\begin{aligned}
& \int_0^{1 / 2} \frac{\left(\left(x^2-1\right)+1\right)}{\left(1-x^2\right)^{3 / 2}} d x \\
& \int_0^{1 / 2} \frac{d x}{\left(1-x^2\right)^{3 / 2}}-\int_0^{1 / 2} \frac{d x}{\sqrt{1-x^2}} \\
& \int_0^{1 / 2} \frac{x^{-3}}{\left(x^{-2}-1\right)^{3 / 2}} d x-\left(\sin ^{-1} x\right)_0^{1 / 2}
\end{aligned}$

Let $x^{-2}-1=t^2 \Rightarrow x^{-3} d x=-t d t$

$\begin{aligned}
& \int_{\infty}^{\sqrt{3}} \frac{-t d t}{t^3}-\frac{\pi}{6}=\int_{\sqrt{3}}^{\infty} \frac{d t}{t^2}-\frac{\pi}{6}=\frac{1}{\sqrt{3}}-\frac{\pi}{6}=\frac{k}{6} \\
& k=2 \sqrt{3}-\pi
\end{aligned}$
Hence, the answer is the option 1 .

Example 4: Let $\mathrm{y}=\mathrm{y}(\mathrm{x})$ be the solution of the differential equation $x d y-y d x=\sqrt{\left(x^2+y^2\right)} d x, x \geqslant 1$, with $\mathrm{y}(1)=0$. If the area bounded by the line $\mathrm{x}=1, x=e^\pi, y=0$ and $\mathrm{y}=\mathrm{y}(\mathrm{x})$ is $\alpha e^{2 \pi}+\beta$, then the va;ue of $10(\alpha+\beta)$ is equal to $\qquad$
1) $2$
2) $4$
3) $6$
4) $8$

Solution

$\begin{aligned}
& x d y-y d x=\sqrt{x^2-y^2} d x \\
& \Rightarrow \int \frac{x d y-y d x}{x^2}=\frac{1}{x} \sqrt{1-\frac{y^2}{x^2}} d x \\
& \Rightarrow \int \frac{d\left(\frac{y}{x}\right)}{\sqrt{1-\left(\frac{y}{x}\right)^2}}=\int \frac{d x}{x} \\
& \Rightarrow \sin ^{-1}\left(\frac{y}{x}\right)=\ln |x|+c \\
& \text { at } x=1, y=0 \Rightarrow c=0 \\
& y=x \sin (\ln x)
\end{aligned}$

$\begin{aligned}& \mathrm{A}=\int_1^{\mathrm{e}^\pi} \mathrm{x} \sin (\ell \mathrm{nx}) \mathrm{dx} \\
& \mathrm{x}=\mathrm{e}^{\mathrm{t}}, \mathrm{dx}=\mathrm{e}^{\mathrm{t}} d \mathrm{dt} \\
& \Rightarrow \int_0^{\pi^2} \mathrm{e}^{2 \mathrm{t}} \sin (\mathrm{t}) \mathrm{dt}=\mathrm{A} \\
& \alpha \mathrm{e}^{2 \pi}+\beta=\left(\frac{\mathrm{e}^{2 t}}{5}(2 \sin \mathrm{t}-\cos \mathrm{t})\right)_0^\pi=\frac{1+\mathrm{e}^{2 \pi}}{5} \\
& \alpha=\frac{1}{5}, \beta=\frac{1}{5} \text { so } 10(\alpha+\beta)=4
\end{aligned}$
Hence, the answer is the option 2.

Example 5: Evaluate the integral of $\int \frac{1}{5 \sqrt{25-4 x^2}} d x$.
1) $\frac{1}{10} \sin ^{-1} \frac{2 x}{5}+C$
2) $-\frac{1}{4 x} \sec ^{-1} \frac{5}{2 x}+C$
3) $\frac{1}{5} \sec ^{-1} \frac{4 x}{5}+C$
4) $-\frac{1}{5} \sec ^{-1} \frac{4 x}{5}+C$

Solution

Given integral

$\int \frac{1}{5 \sqrt{25-4 x^2}} d x$

Substitute $x=\frac{5}{2} \sin \theta$ and $d x=\frac{5}{2} \cos \theta d \theta$.
$\theta=\sin ^{-1} \frac{2 x}{5}$
$\int \frac{1}{5 \sqrt{25-4 x^2}} d x=\int \frac{1}{5 \sqrt{25-\left(4 \times\left(\frac{5}{2} \sin \theta\right)^2\right)}} \frac{5}{2} \cos \theta d \theta$
$\int \frac{1}{\sqrt{25\left(1-\sin ^2 \theta\right)}} \frac{1}{2} \cos \theta d \theta=\frac{1}{2} \int \frac{1}{5 \cos \theta} \times \cos \theta d \theta$
$\frac{1}{10} \int d \theta=\frac{1}{10} \theta+C$
So, it becomes
$\frac{1}{10} \sin ^{-1} \frac{2 x}{5}+C$

Hence, the answer is option (1).

Summary

Indefinite integration is the most elementary process in calculus for seeking antiderivatives of functions. It reverses the process of differentiation, which finds a function whose derivative equals the original function plus an arbitrary constant. Basic rules of integration allow integration with polynomial functions, exponential functions, trigonometric functions, and so on.

Frequently Asked Questions (FAQs)

1. What is integration?

Integration is the reverse process of differentiation.

2. What is the other name of integration?

The other name of integration is antiderivative.

3. What is the difference between an indefinite integral and a definite integral?

An indefinite integral represents a family of functions and includes a constant of integration (C), while a definite integral computes the exact area under a curve between two specific points and results in a single numerical value.

4. Do C is present in definite integrals?

No, only indefinite integrals contain a C in the process of integration.

5. What are the bounds of an indefinite integral?

There are no bounds for an indefinite integral.

6. How do we integrate functions involving square roots?

Integrating functions with square roots often involves substitution or trigonometric substitution. For example, ∫√(a^2 - x^2) dx can be solved using the substitution x = a sin(θ). Understanding these techniques requires a good grasp of trigonometric identities and the relationship between trigonometric and algebraic forms.

7. What is the role of symmetry in simplifying indefinite integrals?

Symmetry can greatly simplify the process of finding indefinite integrals. For even functions (f(-x) = f(x)), the integral will be an odd function plus C. For odd functions (f(-x) = -f(x)), the integral will be an even function plus C. Recognizing symmetry can guide our choice of integration techniques and help verify our results.

8. How does the integration of 1/(1+x^2) relate to the arctangent function?

The integral of 1/(1+x^2) is arctan(x) + C. This relationship exists because the derivative of arctan(x) is 1/(1+x^2). The arctangent function is crucial in integrating rational functions involving x^2 terms in the denominator and appears frequently in physics and engineering applications.

9. How does the method of completing the square help in integration?

Completing the square is useful in integration when dealing with quadratic expressions in the denominator or under a square root. By rewriting the quadratic in the form (x-h)^2 + k, we can often transform the integral into a recognizable form, such as an arctangent or logarithm. This technique is particularly helpful in integrating rational functions and certain trigonometric substitutions.

10. How do we handle integrals involving absolute values?

Integrals involving absolute values often require splitting the integral at the points where the argument of the absolute value changes sign. For each piece, we then integrate the function without the absolute value signs, considering the appropriate sign. This process ensures we account for the piecewise nature of the absolute value function.

11. What is an indefinite integral and how does it differ from a definite integral?

An indefinite integral is the set of all antiderivatives of a function, represented by ∫f(x)dx. It differs from a definite integral in that it doesn't have specific limits of integration and includes a constant of integration (C). The indefinite integral represents a family of functions, while a definite integral calculates the area under a curve between two specific points.

12. Why do we add a constant C when writing indefinite integrals?

We add a constant C to indefinite integrals because the derivative of any constant is zero. This means that when we find an antiderivative, there could be infinitely many functions that differ only by a constant. The +C represents all these possible constants, ensuring we capture the entire family of antiderivatives.

13. How does the power rule for indefinite integrals work, and why does it have an exception?

The power rule for indefinite integrals states that ∫x^n dx = (x^(n+1))/(n+1) + C, where n ≠ -1. It works by increasing the power by 1 and dividing by the new power. The exception for n = -1 exists because this would lead to division by zero. In this case, we use the natural logarithm instead: ∫(1/x)dx = ln|x| + C.

14. Can you explain the relationship between differentiation and indefinite integration?

Differentiation and indefinite integration are inverse operations. If f(x) is a function and F(x) is its indefinite integral, then f(x) = d/dx[F(x)], and F(x) = ∫f(x)dx + C. This relationship is the foundation of the Fundamental Theorem of Calculus and allows us to check our integration work by differentiating the result.

15. How do we integrate exponential functions, and why does e^x have a special property?

To integrate exponential functions, we use the formula ∫a^x dx = (a^x)/ln(a) + C, where a > 0 and a ≠ 1. The function e^x is special because its indefinite integral is itself plus C: ∫e^x dx = e^x + C. This unique property makes e^x particularly useful in calculus and differential equations.

16. What is the significance of the natural logarithm in integration?

The natural logarithm (ln) is significant in integration because it's the antiderivative of 1/x: ∫(1/x)dx = ln|x| + C. It also appears in the integration of exponential functions and is crucial for integration by substitution. The natural log's inverse relationship with e^x makes it a fundamental tool in calculus.

17. How do trigonometric functions behave under indefinite integration?

Trigonometric functions have specific integration rules:

18. Why does integrating sec^2(x) result in tan(x)?

Integrating sec^2(x) results in tan(x) + C because the derivative of tan(x) is sec^2(x). This relationship comes from the identity sec^2(x) = 1 + tan^2(x) and the chain rule. It's a key example of how understanding derivatives helps in finding antiderivatives.

19. What is the significance of u-substitution in indefinite integration?

U-substitution is a powerful technique for simplifying complex integrals by replacing a part of the integrand with a new variable u. It's based on the chain rule of differentiation and is particularly useful for integrating composite functions. U-substitution allows us to transform difficult integrals into simpler, recognizable forms.

20. How do we integrate rational functions?

Integrating rational functions often involves partial fraction decomposition. We break the complex fraction into simpler fractions, which we can then integrate individually. The process involves finding the roots of the denominator, setting up a system of equations, and solving for unknown coefficients. This technique is crucial for integrating many functions that appear in real-world applications.

21. What is integration by parts, and when is it useful?

Integration by parts is a technique based on the product rule of differentiation. It's useful when integrating products of functions, especially when one function becomes simpler when differentiated and the other becomes simpler when integrated. The formula is ∫u dv = uv - ∫v du, where u and dv are chosen strategically to simplify the integral.

22. What are improper integrals, and how do they relate to indefinite integrals?

Improper integrals are definite integrals that involve infinite limits or have discontinuities in the integrand. They're evaluated using limits of definite integrals. While they're not indefinite integrals, understanding indefinite integrals is crucial for solving improper integrals, as we often need to find an antiderivative before taking the limit.

23. What is the significance of the constant of integration in practical applications?

The constant of integration (C) represents the initial condition in many physical problems. For example, in kinematics, when integrating acceleration to find velocity, C represents the initial velocity. In electrical circuits, it might represent the initial charge on a capacitor. Determining the value of C often requires additional information about the specific problem context.

24. How do logarithmic functions behave under integration?

The integral of 1/x is ln|x| + C, but for other logarithmic functions, we often use integration by parts. For example, ∫ln(x)dx = x ln(x) - x + C. Understanding the relationship between exponential and logarithmic functions is key to integrating these types of expressions.

25. What is the relationship between indefinite integrals and differential equations?

Indefinite integrals are closely related to solving first-order differential equations. The process of finding an indefinite integral is essentially solving the differential equation dy/dx = f(x). This connection highlights the importance of integration in modeling real-world phenomena described by differential equations.

26. How do we integrate piecewise functions?

To integrate piecewise functions, we integrate each piece separately over its domain and then combine the results. It's crucial to consider the points where the function changes and to ensure continuity of the antiderivative at these points. This often involves determining appropriate constants of integration for each piece.

27. What is the significance of the Fundamental Theorem of Calculus in understanding indefinite integrals?

The Fundamental Theorem of Calculus connects differentiation and integration, stating that if F(x) is an antiderivative of f(x), then ∫a^b f(x)dx = F(b) - F(a). This theorem shows that indefinite integration (finding antiderivatives) is the key to evaluating definite integrals, highlighting the importance of mastering indefinite integral techniques.

28. How do we integrate inverse trigonometric functions?

Integrating inverse trigonometric functions often requires integration by parts or clever substitutions. For example, ∫arcsin(x)dx = x arcsin(x) + √(1-x^2) + C. These integrals are important in physics and engineering, particularly in problems involving periodic motion or wave phenomena.

29. What is the significance of reduction formulas in integration?

Reduction formulas are recursive relationships that allow us to express complex integrals in terms of simpler ones. They're particularly useful for integrating powers of trigonometric functions, like ∫sin^n(x)dx. These formulas demonstrate the interconnectedness of integrals and can simplify seemingly difficult problems.

30. What is the role of complex numbers in certain indefinite integrals?

Complex numbers can simplify certain real-valued integrals, especially those involving trigonometric functions. For example, ∫sec(x)dx can be solved using complex logarithms. While the final result is real, the intermediate steps may involve complex numbers, showcasing the deep connection between complex analysis and real integration.

31. What is the significance of the integrating factor method in solving differential equations?

The integrating factor method, while primarily used for solving differential equations, is deeply connected to indefinite integration. It involves finding a function that, when multiplied by the differential equation, makes it exactly integrable. This technique showcases how understanding integration patterns can solve complex differential equations.

32. How do we handle integrals involving infinite series?

Integrating infinite series term by term is possible under certain conditions of uniform convergence. This process often involves interchanging the order of integration and summation, which requires justification using theorems from analysis. It's a powerful technique that connects integration with series and highlights the importance of understanding convergence.

33. What is the relationship between indefinite integrals and area under curves?

While indefinite integrals don't directly give the area under a curve (that's the role of definite integrals), they are crucial in finding areas. The Fundamental Theorem of Calculus shows that if F(x) is an antiderivative of f(x), then the area under f(x) from a to b is F(b) - F(a). This connection emphasizes the practical importance of mastering indefinite integration techniques.

34. How do we integrate functions involving logarithms with different bases?

To integrate functions with logarithms of different bases, we often use the change of base formula: log_a(x) = ln(x) / ln(a). This allows us to express all logarithms in terms of natural logarithms, which we can then integrate using known techniques. This approach demonstrates the central role of the natural logarithm in integration.

35. What is the significance of the method of partial fractions in integration?

Partial fraction decomposition is a powerful technique for integrating rational functions. It involves breaking a complex fraction into a sum of simpler fractions, each of which can be integrated individually. This method is crucial in many areas of applied mathematics and engineering, particularly in solving differential equations and analyzing electrical circuits.

36. How do we handle integrals involving hyperbolic functions?

Hyperbolic functions (sinh, cosh, tanh, etc.) have integration rules similar to their trigonometric counterparts. For example, ∫cosh(x)dx = sinh(x) + C. Understanding the relationships between hyperbolic functions and their derivatives is key to integrating them. These functions are particularly important in physics and engineering applications.

37. What is the role of substitution in simplifying indefinite integrals?

Substitution is a fundamental technique in integration, based on the chain rule of differentiation. It involves replacing a complicated part of the integrand with a simpler variable. This method is particularly useful for integrating composite functions and can often transform a difficult integral into a familiar form.

38. How do we integrate functions involving the square root of quadratic expressions?

Integrals involving √(ax^2 + bx + c) often require trigonometric substitution. The choice of substitution depends on the sign of a and the discriminant (b^2 - 4ac). This technique transforms the integral into a trigonometric form, which can then be solved using standard trigonometric integrals.

39. What is the significance of integration by parts in solving recursive integrals?

Integration by parts can be used to set up recursive relationships for certain types of integrals. For example, in evaluating ∫x^n e^x dx, we can use integration by parts repeatedly to express the integral in terms of simpler integrals of the same form. This technique is powerful for solving integrals that seem to resist direct integration.

40. What is the significance of the method of undetermined coefficients in integration?

The method of undetermined coefficients, while more commonly used in differential equations, can be applied to find antiderivatives of certain functions. It involves assuming a general form for the antiderivative and then determining the coefficients by differentiation and comparison. This method highlights the interconnectedness of differentiation and integration.

41. How do we handle integrals involving products of trigonometric and polynomial functions?

Integrals involving products of trigonometric and polynomial functions often require a combination of techniques, such as integration by parts and trigonometric identities. For example, ∫x sin(x)dx can be solved using integration by parts. These types of integrals are common in physics, particularly in problems involving oscillations and waves.

42. What is the role of complex integration in solving real-valued indefinite integrals?

Complex integration techniques can sometimes simplify real-valued integrals, especially those involving trigonometric functions. For instance, integrals of rational functions of

43. How do parametric equations relate to indefinite integrals?

When dealing with parametric equations, we can find the area under a curve using the formula ∫y dx = ∫y(dt/dx)dt. This involves expressing both x and y in terms of a parameter t and then integrating. Understanding this connection helps in solving problems in physics and engineering where parametric representations are common.

44. How do we integrate functions involving the floor or ceiling function?

Integrating functions with floor or ceiling functions typically involves breaking the integral into pieces at integer points. Within each interval, the floor or ceiling function is constant, allowing us to integrate. This process highlights the importance of understanding piecewise functions and discontinuities in integration.

45. How do we handle integrals involving rational functions of sine and cosine?

Integrals involving rational functions of sine and cosine can often be simplified using the substitution u = tan(x/2). This substitution, known as the Weierstrass substitution, transforms trigonometric functions into algebraic ones, allowing us to use techniques for rational functions.

46. What is the role of symmetry in evaluating certain indefinite integrals?

Symmetry can simplify the integration process. For even functions (f(-x) = f(x)), the indefinite integral will be an odd function plus a constant. For odd functions (f(-x) = -f(x)), the indefinite integral will be an even function plus a constant. Recognizing these symmetries can guide our approach and help verify our results.

47. How do we integrate functions involving inverse hyperbolic functions?

Inverse hyperbolic functions (arsinh, arcosh, artanh) have specific integration rules, similar to inverse trigonometric functions. For example, ∫arsinh(x)dx = x arsinh(x) - √(x^2 + 1) + C. These functions appear in many physical and engineering applications, particularly those involving exponential growth or decay.