Integration by Parts - Formula, Derivation, Applications, Examples

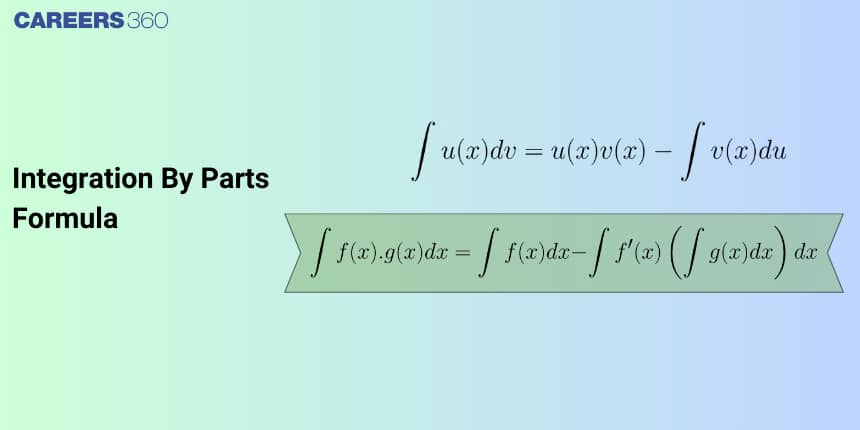
Integration by Parts – Definition, Formula, Proof

Integration acts as the reverse process of differentiation. While differentiation measures the rate of change of a function, integration helps us recover the original function whose derivative is given. In simple terms, if you already know how fast something is changing, integration helps you find what the quantity itself is.

For example:
$\frac{d}{dx}(\sin x)=\cos x$
$\frac{d}{dx}(x^2)=2x$
$\frac{d}{dx}(e^x)=e^x$

When we need to integrate the product of two different types of functions, direct integration doesn’t always work smoothly — and that’s exactly where Integration by Parts becomes a powerful technique.

What Is Integration by Parts?

To evaluate the integral of a product of two functions, say $u(x)$ and $v(x)$, we apply the Integration by Parts formula:

Integration by Parts Formula

$\int u , v , dx = u \int v , dx - \int \left(\frac{du}{dx} \int v , dx\right) dx$

In words:
Integral of (first function × second function) = (first function × integral of second function) – integral of (derivative of first function × integral of second function).

This formula becomes especially useful when the product contains functions like logarithmic, algebraic, exponential, or trigonometric identities.

Derivation of Integration by Parts (Step-by-Step Proof)

Let $h(x)=f(x)\cdot g(x)$.
Using the product rule of differentiation:

$h'(x)=f'(x)g(x)+g'(x)f(x)$

Now integrate both sides:

$\int h'(x) , dx = \int {g(x) f'(x) + f(x) g'(x)} dx$

This gives:

$h(x)=f(x) g(x)=\int g(x) f'(x) , dx +\int f(x) g'(x) , dx$

Rearranging:

$\int f(x) g'(x) , dx = f(x) g(x) - \int g(x) f'(x) , dx$

Now substitute:

$u=f(x)$
$v = g'(x)$
$g(x)=\int v , dx$

Thus we obtain the standard Integration by Parts formula:

$\int u v , dx = u \int v , dx - \int \left(\frac{du}{dx} \int v , dx\right) dx$

How to Choose $u$ and $v$? (ILATE Rule)

Choosing the right function as $u$ is crucial. We use the ILATE preference rule:

ILATE Order

1. I – Inverse Trigonometric Functions

2. L – Logarithmic

3. A – Algebraic

4. T – Trigonometric Functions

5. E – Exponential

Whichever function appears earlier in this list is selected as $u$.

Example:
For $\int x \log x , dx$,

• log is higher priority than algebraic
  → choose $u=\log x$.

Special Applications of Integration by Parts

This section explains the most effective shortcuts and identities in Integration by Parts, focusing on how the method can be applied strategically to exponential functions, trigonometric expressions, and composite integrals. By using integration by parts smartly, complex-looking integrals become simpler and more manageable, making this technique extremely useful for Class 12 board exams and competitive entrance exams. You’ll also learn how these identities reduce lengthy calculations, improve speed, and help build confidence in solving exam-oriented integration problems with accuracy.

Evaluating $\int e^x {f(x)+f'(x)} dx$

A very interesting application is:

$\int e^x{f(x)+f'(x)} dx = e^x f(x) + C$

Proof

Start with:

$\int e^x{f(x)+f'(x)} dx = \int e^x f(x) dx + \int e^x f'(x) dx$

For the first integral, apply Integration by Parts with
$u=f(x)$ and second function $e^x$:

$f(x)e^x - \int f'(x)e^x dx + \int e^x f'(x) dx$

The last two integrals cancel out, giving:

$= f(x)e^x + C$

Thus,

$\int e^x{f(x)+f'(x)} dx = e^x f(x)+C$

General Formula for Integration by Parts

A more general and powerful identity is:

$\int e^{g(x)} { f(x)g'(x) + f'(x)} dx = f(x)e^{g(x)} + C$

This shows how combining exponential and composite functions simplifies dramatically.

Integration of $e^{ax} \sin bx$ and $e^{ax} \cos bx$

These integrals appear frequently in competitive exams and require repeated use of Integration by Parts.

Integral of $e^{ax} \sin bx$

Let
$I=\int e^{ax} \sin bx , dx$

Choose $\sin bx$ as first function and $e^{ax}$ as second:

$I=\frac{1}{a} e^{ax} \sin bx - \frac{b}{a} \int e^{ax} \cos bx , dx$

Apply Integration by Parts again inside the remaining integral.
Finally, after rearranging:

$I=\frac{e^{ax}}{a^2+b^2}(a \sin bx - b \cos bx) + C$

Integral of $e^{ax} \cos bx$

Similarly:

$\int e^{ax} \cos bx , dx = \frac{e^{ax}}{a^2+b^2}(a \cos bx + b \sin bx) + C$

These results form a standard pair that students should memorize.

Example Result

$\int e^{\tan^{-1}x}\left[\frac{x^n+1}{x^2+1}+nx^{n-1}\right] dx = e^{\tan^{-1}x}(x^n+1) + C$

This follows from the general formula:

$\int e^{g(x)}{f(x)g'(x)+f'(x)} dx = f(x)e^{g(x)} + C$

Such integrals commonly appear in higher-level calculus and engineering mathematics.

Step-by-Step Method to Solve Integrals Using Integration by Parts

Integration by parts is a standard technique in Class 12 calculus used to evaluate integrals involving the product of two functions, such as algebraic × logarithmic, algebraic × trigonometric, or algebraic × exponential functions.

Step 1: Identify the Two Functions in the Integral

Start by rewriting the given integral as a product of two functions:

$\int u , dv$

Here:

• $u$ is the function to be differentiated

• $dv$ is the function to be integrated

Choosing the correct $u$ and $dv$ is crucial for simplifying the integral.

Step 2: Choose $u$ and $dv$ Using the ILATE Rule

To select $u$ correctly, use the ILATE rule, which gives priority in the following order:

• I – Inverse trigonometric functions

• L – Logarithmic functions

• A – Algebraic functions

• T – Trigonometric functions

• E – Exponential functions

The function appearing earlier in ILATE is chosen as $u$, and the remaining part becomes $dv$. This rule helps reduce complexity and is widely used in board exam problems.

Step 3: Differentiate $u$ and Integrate $dv$

Once $u$ and $dv$ are chosen:

Differentiate $u$ to find
$du = \dfrac{du}{dx} , dx$

Integrate $dv$ to find
$v = \int dv$

This step prepares all the components needed for applying the integration by parts formula.

Step 4: Apply the Integration by Parts Formula

Substitute $u$, $du$, $v$, and $dv$ into the formula:

$\int u , dv = uv - \int v , du$

This formula converts the original integral into a simpler integral, which is usually easier to evaluate.

Step 5: Simplify and Evaluate the Remaining Integral

Evaluate the new integral $\int v , du$ carefully. In some cases, integration by parts may need to be applied more than once, especially for integrals involving powers of $x$ with trigonometric or exponential functions.

Finally, simplify the expression to obtain the required result.

Step 6: Add Constant of Integration (If Required)

For indefinite integrals, always add the constant of integration $C$ at the end:

$+ C$

This step is essential for full marks in Class 12 board examinations.

Solved Examples Based On Integration by Parts:

Example 1: The integral $\int x \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) d x(x>0)$ is equal to:
${ }_1-x+\left(1+x^2\right) \tan ^{-1} x+c$
2) $x-\left(1+x^2\right) \cot ^{-1} x+c$
3) $-x+\left(1+x^2\right) \cot ^{-1} x+c$
4) $x-\left(1+x^2\right) \tan ^{-1} x+c$

Solution

As learned in the concept

Integration By PARTS -

Let $u$ and $v$ are two functions then

$
\int u \cdot v d x=u \int v d x-\int\left(\frac{d u}{d x} \int v d x\right) d x
$

- wherein

Where $u$ is the lst function $v$ is the Ind function

$
\begin{aligned}
& \text { Put } x=\tan \theta ; d x=\sec ^2 \theta d \theta \\
& \int x \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) d x(x>0) \\
& \int \tan \theta\left[\cos ^{-1}\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)\right]\left(\sec ^2 \theta d \theta\right) \\
& \int \tan \theta\left[\cos ^{-1}(\cos 2 \theta)\right]\left(\sec ^2 \theta d \theta\right) \\
& \int \tan \theta \cdot 2 \theta \sec ^2 \theta d \theta=2 \int \theta\left(\tan \theta \sec ^2 \theta\right) d \Theta
\end{aligned}
$
Put $\tan \theta=t$ we get $\sec ^2 \theta d \theta=d t$

$
\begin{aligned}
& 2 \int \tan ^{-1} t(t) d t \\
& 2 \int t \cdot \tan ^{-1} t \cdot d t
\end{aligned}
$

Using by parts

$\begin{aligned}
& 2\left[\frac{t^2}{2} \cdot \tan ^{-1} t-\int \frac{1}{1+t^2} \cdot \frac{t^2}{2} \cdot d t\right] \\
& t^2 \cdot \tan ^{-1} t-\int \frac{1}{1+t^2} \cdot t^2 \cdot d t \\
& t^2 \cdot \tan ^{-1} t-\int \frac{t^2+1-1}{1+t^2} \cdot d t \\
& t^2 \cdot \tan ^{-1} t-\int\left[1-\frac{1}{1+t^2}\right] \cdot d t \\
& t^2 \cdot \tan ^{-1} t-\left[t-\tan ^{-1} t\right] \\
& \Rightarrow x=t \\
& x=\tan \theta \quad \& \quad \tan \theta=t \\
& \int x \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) d x=x^2 \tan ^{-1} x-x+\tan ^{-1} x+C
\end{aligned}$
Hence, the answer is the option 1.

Example 2: If $\int f(x) d x=\Psi(x)$, then $\int x^5 f\left(x^3\right) d x$ is equal to:
1) $\frac{1}{3}\left[x^3 \Psi\left(x^3\right)-\int x^3 \Psi\left(x^3\right) d x\right]+C$
2) $\frac{1}{3}\left[x^3 \Psi\left(x^3\right)-\int x^2 \Psi\left(x^3\right) d x\right]+C$
3) $\frac{1}{3} x^3 \Psi\left(x^3\right)-3 \int x^3 \Psi\left(x^3\right) d x+C$
4) $\frac{1}{3} x^3 \Psi\left(x^3\right)-\int x^2 \Psi\left(x^3\right) d x+C$

Solution
Using Integration By Parts,

$\begin{aligned}
& \int f(x) d x=\Psi(x) \int x^5 f\left(x^3\right) d x=\frac{1}{3} \int\left(3 x^2\right) \cdot x^3 f\left(x^3\right) d x P u t x^3=t ; 3 x^2 d x=d t \\
& \frac{1}{3} \int t f(t) d t=\frac{1}{3}\left[t \int f(t) d t-\int 1 \int f(t) d t\right]
\end{aligned}$
Replace $t$ by $x^3$

$I=\frac{1}{3} x^3 \Psi\left(x^3\right)-\frac{1}{3} \int \Psi\left(x^3\right) d t=\frac{1}{3} x^3 \Psi\left(x^3\right)-\frac{1}{3} \int 3 x^2 d x . \Psi\left(x^3\right)=\left[\frac{1}{3} x^3 \Psi\left(x^3\right)-\int x^2 \Psi\left(x^3\right) d x\right]+c$
Hence, the answer is the option (4).

Example 3: Let $f(x)=\int \frac{\sqrt{x}}{(1+x)^2} d x(x \geqslant 0)$.Then $f(3)-f(1)$ is equal to:
1) $-\frac{\pi}{12}+\frac{1}{2}+\frac{\sqrt{3}}{4}$
2) $\frac{\pi}{6}+\frac{1}{2}+\frac{\sqrt{3}}{4}$
3) $-\frac{\pi}{6}+\frac{1}{2}+\frac{\sqrt{3}}{4}$
4) $\frac{\pi}{12}+\frac{1}{2}-\frac{\sqrt{3}}{4}$

Solution
$f(x)=\int_1^3 \frac{\sqrt{x} d x}{(1+x)^2}=\int_1^{\sqrt{3}} \frac{t \cdot 2 t d t}{\left(1+t^2\right)^2}($ put $\sqrt{x}=t)$
$=\left(-\frac{t}{1+t^2}\right)_t^{\sqrt{3}}+\left(\tan ^{-1} t\right)_1^{\sqrt{3}}$ [Applying by parts ]
$=-\left(\frac{\sqrt{3}}{4}-\frac{1}{2}\right)+\frac{\pi}{3}-\frac{\pi}{4}$
$=\frac{1}{2}-\frac{\sqrt{3}}{4}+\frac{\pi}{12}$

Hence, the answer is the option 4.

Example 4: The integral $\int\left(\frac{x}{x \sin +\cos x}\right)^2 d x$ is equal to (where C is constant of integration).
1) $\tan x-\frac{x \sec x}{x \sin x+\cos x}+C$
2) $\sec x \frac{x \tan x}{x \sin x+\cos x}+C$
3) $\sec x-\frac{x \tan x}{x \sin x+\cos x}+C$
4) $\tan x+\frac{x \sec x}{x \sin x+\cos x}+C$

Solution

$\begin{aligned}
& \int\left(\frac{x}{x \sin x+\cos x}\right)^2 d x=\int\left(\frac{x}{\cos x}\right) \cdot \frac{x \cos x d x}{(x \sin x+\cos x)^2} \\
& =\frac{x}{\cos x}\left(-\frac{1}{x \sin x+\cos x}\right)+\int\left(\frac{\cos x+x \sin x}{\cos ^2 x}\right)\left(\frac{1}{x \sin x+\cos x}\right) d x \\
& =-\frac{x \sec x}{x \sin x+\cos x}+\int \sec ^2 x d x \\
& =-\frac{x \sec x}{x \sin x+\cos x}+\tan x+C
\end{aligned}$
Hence, the answer is option (1).

Example 5 :

$\int_{\mathrm{If}}^1\left(e^{2 x}+2 e^x-e^{-x}-1\right) e^{\left(e^x+e^{-x}\right)} d x=g(x) e^{\left(e^x+e^{-x}\right)}+c$

1) e
2) $e^2$
3) 1
4) 2

Solution:

$\begin{aligned}
& e^{2 x}+2 e^x-e^{-x}-1 \\
& =e^x\left(e^x+1\right)-e^{-x}\left(e^x+1\right)+e^x \\
& \left.=\left[\left(e^x+1\right)\right]\left(e^x-e^{-x}\right)+e^x\right] \\
& \text { so } I=\int\left(e^x+1\right)\left(e^x-e^{-x}\right) e^{e^x+e^{-x}}+\int e^x \cdot e^{e^x+e^{-x}} d x \\
& =\left(e^x+1\right) e^{e^x+e^{-x}}-\int e^x \cdot e^{e^x+e^{-x}} d x+\int e^x \cdot e^{e^x+e^{-x}} d x \\
& =\left(e^x+1\right) e^{e^x+e^{-x}}+C \\
& \therefore g(x)=e^x+1 \Rightarrow g(0)=2
\end{aligned}$

Hence, the answer is option (4).

List of Topics Related to Integration by parts

This section quickly walks you through all the important topics connected to Integration by Parts. It helps you see what to study, how concepts link together, and where this method fits in your overall integration.

Application of Integrals

Integral of Particular Functions

Indefinite Integrals

Integration of irrational functions

Application of Inequality in Definite Integration

NCERT Resources

This section gives you a quick overview of all the essential NCERT support materials you need for mastering Chapter 7 – Integrals. From crisp notes to detailed solutions and advanced exemplar practice, it brings everything under one place to make your preparation easier and more structured.

NCERT Class 12 Maths Notes for Chapter 7 - Integrals

NCERT Class 12 Maths Solutions for Chapter 7 - Integrals

NCERT Class 12 Maths Exemplar Solutions for Chapter 7 - Integrals

Practice Questions based on Integration by parts

This section includes practice questions designed to test your understanding of the Integration by Parts formula and its applications. These questions work great for building confidence through hands-on solving.

Integration By Parts Formula- Practice Question MCQ

We have provided below the practice questions related to different concepts of integration to improve your understanding: