Reduction Formulas For Integration by Parts With Solved Examples

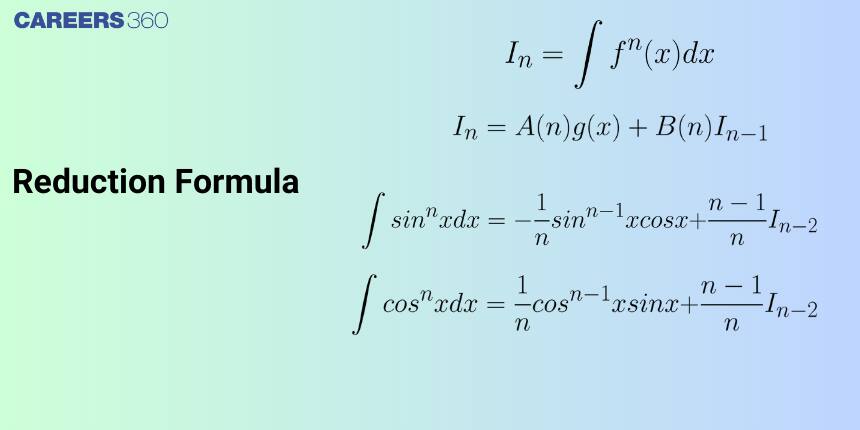
Introduction to Reduction Formulas

Reduction formulas are like the shortcuts of integration — instead of wrestling with higher powers of functions, you break them down step-by-step into easier, lower-order integrals. This technique is incredibly useful in Class 12 calculus, JEE preparation, and any situation where integrals repeat in patterns.

What Is a Reduction Formula?

A reduction formula expresses the integral of a function raised to a power n in terms of an integral with a lower power such as n−1 or n−2.
This repeated reduction continues until the expression becomes a basic integral that can be evaluated directly.

Deriving a Standard Reduction Formula

Example: Derivation for

$ \int x^n e^x , dx $

Using Integration by Parts:
Choose

• $u = x^n$

• $dv = e^x dx$

Then
$du = n x^{n-1} dx$ and $v = e^x$

Applying the formula
$ \int u , dv = uv - \int v , du $

We get:
$ \int x^n e^x dx = x^n e^x - n \int x^{n-1} e^x dx $

This is the required reduction formula, expressing the integral in terms of a lower power.

Reduction Formulas for Trigonometric Integrals

Trigonometric reduction formulas are incredibly useful when you're dealing with higher powers of sine, cosine, tangent, or other trig functions. Instead of integrating directly — which can get messy — these formulas gradually lower the power, making the integral easier step by step. They’re a favorite in competitive exams because they turn long, intimidating expressions into manageable recursive patterns.

Reduction Formula for $ \int \sin^n x , dx $

Let
$ I_n = \int \sin^n x , dx $

Start by rewriting the integrand:
$ I_n = \int \sin^{n-1} x \cdot \sin x , dx $

Using integration by parts and simplifying, you arrive at the classic reduction formula:
$ I_n = -\frac{\sin^{n-1} x \cos x}{n} + \frac{n-1}{n} I_{n-2} $

This means every application drops the power by 2, making it ideal when $n$ is large or even.

Reduction Formula for $ \int \tan^n x , dx $

Let
$ I_n = \int \tan^n x , dx $

Use the identity:
$ \tan^n x = \tan^{n-2} x (\sec^2 x - 1) $

Set $ t = \tan x $, so $ dt = \sec^2 x , dx $.
This transforms a part of the integral into
$ \int \tan^{n-2} x \sec^2 x , dx = \int t^{n-2} , dt $

Finally, the reduction formula becomes:
$ I_n = \frac{\tan^{n-1} x}{n-1} - I_{n-2} $

Example: Solve $ \int \tan^4 x , dx $
You repeatedly apply the reduction formula until the powers drop low enough to integrate directly.

Additional Identities for Simplification

Many trig powers can be simplified before applying reduction formulas using identities like:
$ \sin^4 x = \left(\frac{1 - \cos 2x}{2}\right)^2 $
$ \cos^4 x = \left(\frac{1 + \cos 2x}{2}\right)^2 $

These expansions often reduce the complexity before integration even starts.

Reduction Formula for $ \int \cos^n x , dx $

Let
$ I_n = \int \cos^n x , dx $

Using integration by parts, you get:
$ I_n = \frac{\cos^{n-1} x \sin x}{n} + \frac{n-1}{n} I_{n-2} $

This follows the same pattern as the sine reduction formula — reducing the power by 2 on each iteration.

Reduction Formula for $ \int \cot^n x , dx $

Let
$ I_n = \int \cot^n x , dx $

Use the identity:
$ \cot^2 x = \csc^2 x - 1 $

Choose the substitution $ t = \cot x $, then $ dt = -\csc^2 x , dx $.
After simplification, the formula becomes:
$ I_n = -\frac{\cot^{n-1} x}{n-1} - I_{n-2} $

This stepwise reduction makes even large powers of cot manageable.

Reduction Formula for $ \int \sec^n x , dx $

Let
$ I_n = \int \sec^n x , dx $

Using integration by parts and trig identities, the reduction formula is:
$ I_n = \frac{\sec^{n-2} x \tan x}{n-1} + \frac{n-2}{n-1} I_{n-2} $

This is especially helpful when dealing with even powers of secant.

Reduction Formula for $ \int \csc^n x , dx $

Let
$ I_n = \int \csc^n x , dx $

Following a similar process as secant integrals:
$ I_n = -\frac{\csc^{n-2} x \cot x}{n-1} + \frac{n-2}{n-1} I_{n-2} $

Advanced Reduction Formulas: Mixed Trigonometric Integrals

Mixed trigonometric integrals often show up when you're working with oscillatory functions or solving physics problems involving waves. A general case you’ll encounter is
$ I_{m,n} = \int \cos^m x \sin nx , dx $,
where m and n can be any positive integers. These integrals look messy at first, but reduction formulas help you shrink them step-by-step into simpler versions.

To derive the reduction, use integration by parts by choosing

• $u = \cos^m x$

• $dv = \sin nx,dx$

This choice makes the structure manageable and leads to the following reduction formula:

$ I_{m,n} = -\frac{\cos^m x \cos nx}{m+n} + \frac{m}{m+n} I_{m-1,n-1} $

This result is powerful because it reduces both m and n by 1 at each step. Over repeated applications, the integral eventually collapses into a basic sine–cosine form that can be handled easily.

Additional Useful Results

1. $ \int \cos^m x \cos nx dx = \frac{\cos^m x \sin nx}{m+n} + \frac{m}{m+n} \int \cos^{m-1} x \cos(n-1)x dx $

2. $ \int \sin^m x \sin nx dx = \frac{n \sin^m x \cos nx}{m^2-n^2} - \frac{m \sin^{m-1}x \cos x \cos nx}{m^2-n^2} + \frac{m(m-1)}{m^2-n^2}\int \sin^{m-2}x \sin nx dx $

3. $ \int \sin^m x \cos nx dx = \frac{n \sin^m x \sin nx}{m^2-n^2} - \frac{m \sin^{m-1}x \cos x \cos nx}{m^2-n^2} + \frac{m(m-1)}{m^2-n^2}\int \sin^{m-2}x \cos nx dx $

Solved Examples Based on Integration by Reduction Formula

Example 1: Evaluate $\int \sin ^4 x d x$

1) $\frac{1}{8}+\frac{\sin 4 x}{32}+\frac{\sin 2 x}{2}+C$
2) $\frac{\sin (4 x)-8 \sin (2 x)+12 x}{32}+C$
3) $\frac{1}{8}-\frac{\sin 4 x}{32}+\frac{\sin 2 x}{2}+C$

4) none of these

Solution
$
\begin{aligned}
& I=\int \sin ^4 x d x \\
& \Rightarrow I=\int\left(\frac{1-\cos 2 x}{2}\right)^2 d x \\
& =\frac{1}{4} \int\left(1-2 \cos 2 x+\cos ^2 2 x\right) d x \\
& =\frac{1}{4} x-\frac{1}{2} \int \cos 2 x d x+\frac{1}{4} \int \cos ^2 2 x d x \\
& =\frac{1}{4} x-\frac{1}{4} \sin 2 x+\frac{1}{8}\left(x+\frac{1}{4} \sin (4 x)\right) \\
& =\frac{\sin (4 x)-8 \sin (2 x)+12 x}{32}+C
\end{aligned}
$

Hence, the answer is the option (2).

Example 2: Find the value of $\int \sin ^2 x \cos ^2 x d x$

1) $\frac{x}{2}-\frac{\sin 2 x}{2}+C$
2) $\frac{x}{4}-\frac{\sin 4 x}{4}+C$
3) $\frac{1}{8}\left(x-\frac{1}{4} \sin (4 x)\right)+C$
4) $\frac{x}{2}-\frac{\sin 2 x}{4}+C$

Solution

$=\int \sin ^2 x \cos ^2 x d x=\int \frac{\sin ^2(2 x)}{4} d x=\int \frac{1-\cos (4 x)}{8} d x=\frac{1}{8}\left(x-\frac{1}{4} \sin (4 x)\right)+C$

Hence, the answer is the option (3).

Example 3: $\int\left(\tan ^2 x+\cot ^2 x\right) d x$

1) $\tan x+\cot x+C$

2) $\tan x+\cot x-2+C$

3) $-2 x+\tan (x)-\cot (x)+C$

4) $\sec x+\csc x+C$

Solution

$\begin{aligned} & I=\int \tan ^2(x) d x+\int \cot ^2(x) d x \\ & \int \tan ^2(x) d x=\int-1+\sec ^2(x) d x=-x+\tan (x) \\ & \int \cot ^2(x) d x=\int-1+\csc ^2(x) d x=-x-\cot (x) \\ & I=-2 x+\tan (x)-\cot (x)+C\end{aligned}$

Hence, the answer is the option (3).

Example 4: Integrate $\int \tan ^4 x d x$

1) $\frac{\tan ^3 x}{3}-\tan x+C$
2) $\frac{\tan ^3 x}{3}-\tan x+x+C$
3) $\frac{\tan ^3 x}{3}+C$
4) $\frac{\tan ^3 x}{3}+\tan x+C$

Solution

$\begin{aligned} & \int \tan ^4 x d x \\ & =\int \tan ^2 x\left(\sec ^2 x-1\right) d x \\ & =\int \tan ^2 x \sec ^2 x d x-\int \tan ^2 x d x \\ & =\int \tan ^2 x \sec ^2 x d x-\int\left(\sec ^2 x-1\right) d x \\ & =\frac{\tan ^3 x}{3}-\tan x+x+C\end{aligned}$

Hence, the answer is the option (2).

Example 5: Integrate $\int \cot ^5 x d x$

1) $\frac{\cot ^4 x}{4}-\frac{\cot ^2 x}{2}+C$

2) $-\ln (\csc (x))-\frac{\csc ^4(x)}{4}+\csc ^2(x)+c$

3) $\frac{\cot ^4 x}{4}-\cot ^2 x+\ln \sin x+C$

4)None of these

Solution

$\begin{aligned} & \int \cot ^5 x d x=\int \cot x\left(\csc ^2 x-1\right)^2 d x \\ & u=\csc (x): \mathrm{d} x=-\frac{1}{\cot (x) \csc (x)} \mathrm{d} u \\ & =-\int \frac{\left(u^2-1\right)^2}{u} \mathrm{~d} u \\ & =-\ln (\csc (x))-\frac{\csc ^4(x)}{4}+\csc ^2(x)+c\end{aligned}$

Hence, the answer is the option (2).

List of Topics Related to the Reduction Formulas For Integration by Parts

The section explores important topics that build on reduction formulas used in integration by parts. It offers insights into techniques for simplifying irrational algebraic functions, connecting foundational ideas like indefinite and definite integrals with their practical applications.

Application of Integrals

Integral of Particular Functions

Indefinite Integrals

Integration by parts

Application of Inequality in Definite Integration

NCERT Resources

This section compiles all vital NCERT resources for Chapter 7 – Integrals, offering a one-stop guide for effective learning and exam readiness. From detailed notes and step-by-step solutions to challenging exemplar problems, these materials help build a strong foundation in key integration techniques and boost confidence for both board and competitive exams.

NCERT Class 12 Maths Notes for Chapter 7 - Integrals

NCERT Class 12 Maths Solutions for Chapter 7 - Integrals

NCERT Class 12 Maths Exemplar Solutions for Chapter 7 - Integrals

Practice Questions based on Reduction Formulas For Integration by Parts

This section offers a rich set of custom practice questions exploring reduction formulas and integration by parts. Through hands-on exercises involving different algebraic and irrational integrals, you can steadily enhance your technical skills, deepen your understanding, and gain the confidence needed to tackle challenging integration problems independently.

Reduction Formula- Practice Question MCQ

We have provided below the practice questions related to different concepts of integration to improve your understanding: