Graphs of General Trigonometric Functions

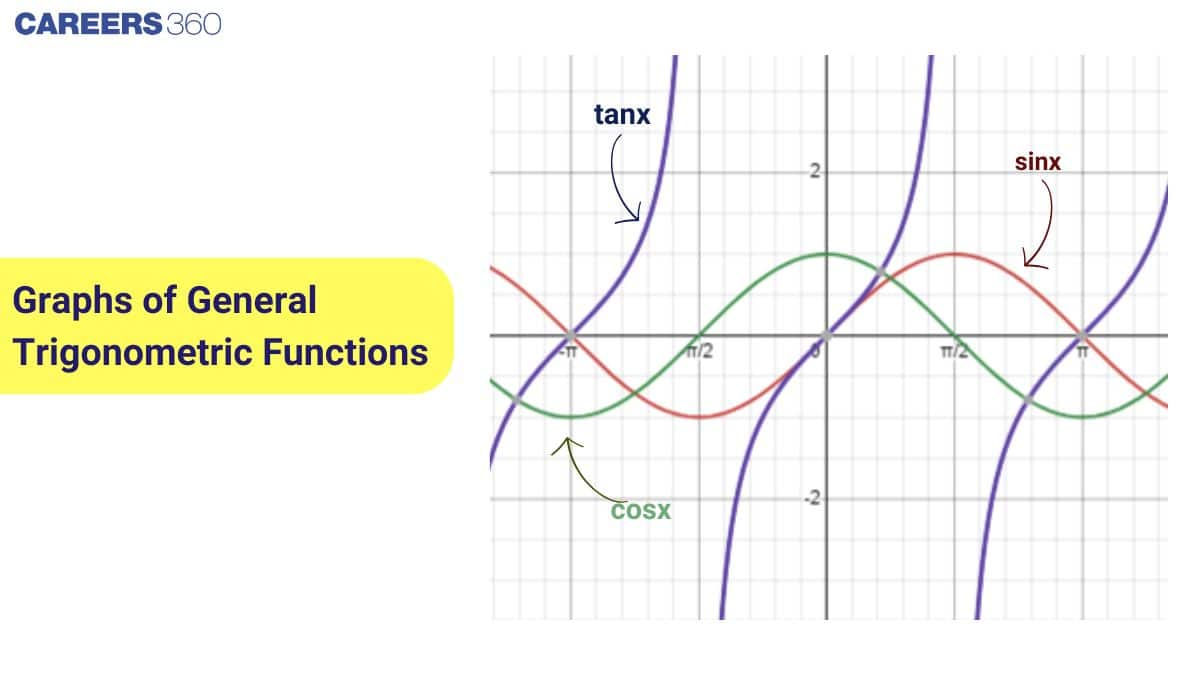
Introduction to Graphs of Trigonometric Functions

Graphs of general trigonometric functions like $\sin x$, $\cos x$, and $\tan x$ show wave-like patterns that repeat, helping us understand amplitude, periodicity, and phase shift. Mastering the sine, cosine tangent graphs and other trigonometric functions graphs is essential for Class 11 Maths and exams like JEE.

What Are Trigonometric Function Graphs?

Trigonometric function graphs show how functions like $\sin x$, $\cos x$, and $\tan x$ change as the value of $x$ varies. These graphs help us clearly see important features such as periodic behavior, symmetry, maximum and minimum values, and repeating wave patterns, which are hard to understand using formulas alone.

By studying graphs of $\sin x$, $\cos x$, $\tan x$, $\sec x$, $\csc x$, and $\cot x$, we can understand how each trigonometric function behaves over different intervals. Graphing these functions also helps us analyze amplitude, period, phase shift, and vertical shift, making it easier to draw and interpret general trigonometric graphs accurately.

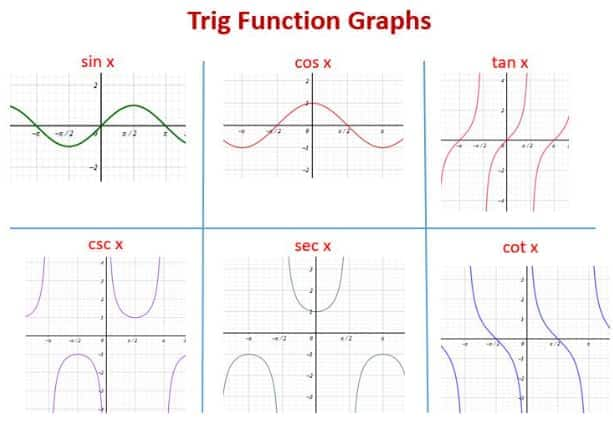
Standard Graphs of Sine, Cosine, and Tangent Functions

The standard graphs of $\sin x$, $\cos x$, and $\tan x$ are the most important graphs in trigonometry. These functions show repeating wave-like patterns, clearly demonstrating the periodic nature of trigonometric functions. Understanding these standard graphs forms the foundation for learning graphs of general trigonometric functions, solving trigonometric equations, analyzing periodic behavior, and preparing for board exams and competitive exams like JEE.

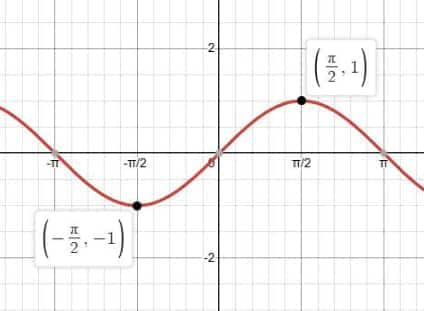
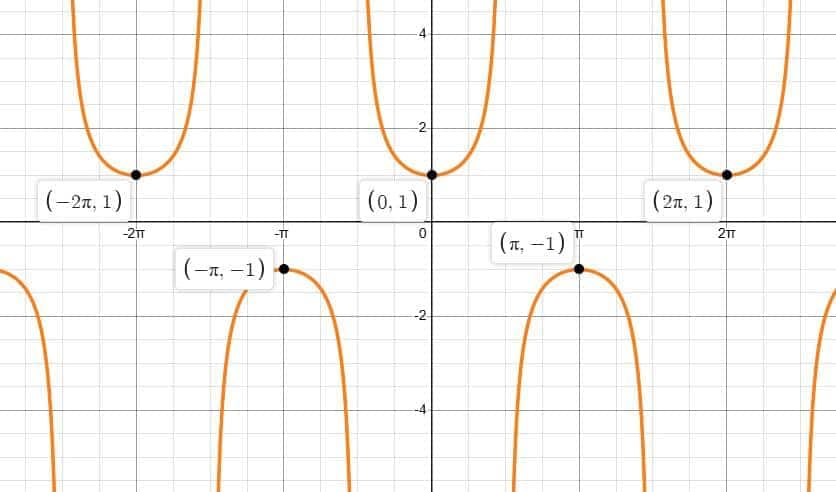
Graph of the Sine Function ($\sin x$)

The graph of $\sin x$ is a smooth and continuous curve that starts at the origin and oscillates between fixed maximum and minimum values. It is one of the most basic and widely used examples among the graphs of trigonometric functions.

Sine is defined as the ratio of the opposite side (perpendicular) to the hypotenuse with respect to a given angle.

Equation of the Sine Function

$y = f(x) = \sin x$

In the sine graph, the angle values are taken on the $x$-axis, and the corresponding values of $y = \sin x$ are plotted on the $y$-axis.

Domain and Range of $\sin x$

• Domain: $\mathbb{R}$

• Range: $[-1, 1]$

This means the sine function is defined for all real numbers, but its values always lie between $-1$ and $1$.

Period of the Sine Function

The sine function completes one full cycle over an interval of length $2\pi$.

• Period: $2\pi$

The graph drawn over the interval $[0, 2\pi]$ repeats itself infinitely to the left and right, showing the periodic nature of $\sin x$.

Zeros of the Sine Function

The roots (zeroes) of the sine function occur when:

$x = n\pi$, where $n \in \mathbb{Z}$

At these points, the sine graph crosses the $x$-axis.

Maximum and Minimum Values of $\sin x$

• Maximum value: $\sin x = 1$ at $x = \dfrac{\pi}{2}$

• Minimum value: $\sin x = -1$ at $x = \dfrac{3\pi}{2}$

Amplitude of the Sine Function

• Amplitude: $1$

The amplitude represents the maximum distance of the graph from the $x$-axis.

Symmetry of the Sine Graph

Since $\sin(-x) = -\sin x$, the sine function is an odd function.

As a result, the graph of $\sin x$ is symmetric about the origin, which is an important property used in graph analysis and problem solving.

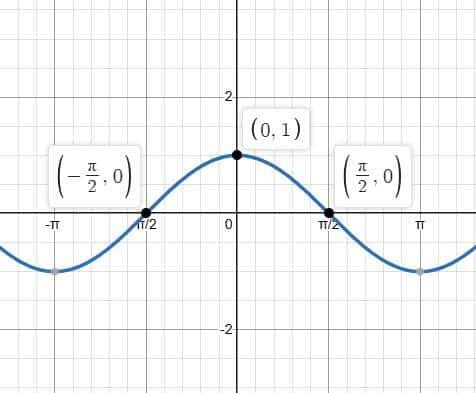
Graph of the Cosine Function ($\cos x$)

The graph of $\cos x$ is one of the standard trigonometric function graphs and closely resembles the sine graph, except that it starts at its maximum value. Like sine, the cosine function shows a smooth, repeating wave pattern, making it a key part of the graphs of general trigonometric functions used in mathematics and physics.

Cosine is defined as the ratio of the adjacent side (base) to the hypotenuse for a given angle.

Equation of the Cosine Function

$y = f(x) = \cos x$

In the cosine graph, the angle values are plotted on the $x$-axis, and the corresponding values of $y = \cos x$ are plotted on the $y$-axis.

Relationship Between Sine and Cosine Graphs

The cosine function is related to the sine function by the identity:

$\sin(x + 90^\circ) = \cos x$

This shows that the graph of $\cos x$ is the same as the graph of $\sin x$ shifted left by $90^\circ$ (or $\dfrac{\pi}{2}$ radians).

Domain and Range of $\cos x$

• Domain: $\mathbb{R}$

• Range: $[-1, 1]$

The cosine function is defined for all real numbers, and its values always lie between $-1$ and $1$.

Period of the Cosine Function

The cosine function completes one full cycle over an interval of length $2\pi$.

• Period: $2\pi$

The graph repeats itself continuously to both the left and right of the origin.

Zeros of the Cosine Function

The roots (zeroes) of the cosine function occur at:

$x = \dfrac{(2n + 1)\pi}{2}$, where $n \in \mathbb{Z}$

At these points, the cosine graph intersects the $x$-axis.

Maximum and Minimum Values of $\cos x$

• Maximum value: $\cos x = 1$ at $x = 0, 2\pi, 4\pi, \dots$

• Minimum value: $\cos x = -1$ at $x = \pi$

Amplitude of the Cosine Function

• Amplitude: $1$

The amplitude represents the maximum vertical distance of the graph from the $x$-axis.

Symmetry of the Cosine Graph

Since $\cos(-x) = \cos x$, the cosine function is an even function.

Therefore, the graph of $\cos x$ is symmetric about the $y$-axis, which is an important property in graph analysis and problem solving.

What are the characteristics of the graphs of trigonometric functions? What are the properties of the graphs of sin x and cos x? The graphs of sin x and cos x are both periodic. They repeat every 360° (2π radians) The angle will always be on the x-axis.

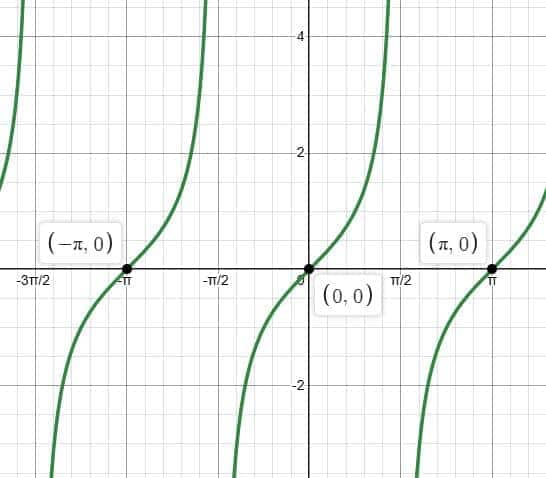
Graph of the Tangent Function ($\tan x$)

The graph of $\tan x$ is quite different from the graphs of sine and cosine. Unlike smooth wave patterns, the tangent graph shows sharp increases and discontinuities due to the presence of vertical asymptotes. Because of this behavior, the tangent function is especially useful for understanding rapid changes, discontinuous graphs, and asymptotic behavior in trigonometry.

Tangent is defined as the ratio of the opposite side (perpendicular) to the adjacent side (base) for a given angle.

Equation of the Tangent Function

$y = f(x) = \tan x$

In the graph of the tangent function, angle values are taken along the $x$-axis, and the corresponding values of $y = \tan x$ are plotted on the $y$-axis.

Domain and Range of $\tan x$

Domain of $\tan x$: $x \in \mathbb{R} - \left\{ \dfrac{\pi}{2} + n\pi \mid n \in \mathbb{Z} \right\}$

The tangent function is not defined at these values because $\cos x = 0$ there.

Range: $\mathbb{R}$

This means $\tan x$ can take any real value.

Period of the Tangent Function

The tangent function completes one full cycle over an interval of length $\pi$.

• Period: $\pi$ (or $180^\circ$)

This shorter period distinguishes the tangent graph from sine and cosine graphs, which have a period of $2\pi$.

Vertical Asymptotes of $\tan x$

The vertical asymptotes of the tangent graph occur at:

$x = \dfrac{\pi}{2} + n\pi$, where $n \in \mathbb{Z}$

Between each pair of asymptotes, the graph rises continuously from negative infinity to positive infinity.

Behavior of the Tangent Graph

The function $\tan x$ increases continuously in each interval such as:

$(-\dfrac{3\pi}{2}, -\dfrac{\pi}{2})$,
$(-\dfrac{\pi}{2}, \dfrac{\pi}{2})$,
$(\dfrac{\pi}{2}, \dfrac{3\pi}{2})$, and so on.

In each interval, the graph shows a steep upward curve, highlighting the unbounded nature of the tangent function.

Zeros of the Tangent Function

The roots (zeroes) of $\tan x$ occur at:

$x = n\pi$, where $n \in \mathbb{Z}$

At these points, the tangent graph crosses the $x$-axis.

Amplitude of the Tangent Function

• Amplitude: Not defined

Since the tangent graph has no maximum or minimum value and extends to $\pm\infty$, amplitude is not defined for $\tan x$.

Symmetry of the Tangent Graph

Since: $\tan(-x) = -\tan x$ the tangent function is an odd function.

As a result, the graph of $\tan x$ is symmetric about the origin, which is useful when sketching graphs and solving equations.

Graphs of Reciprocal Trigonometric Functions

The reciprocal trigonometric functions—$\csc x$, $\sec x$, and $\cot x$—have graphs that are closely related to the graphs of $\sin x$, $\cos x$, and $\tan x$. These graphs contain vertical asymptotes and are defined only where their corresponding base functions are non-zero. Understanding the graphs of cosec, sec, and cot functions is important for analyzing undefined values, solving advanced trigonometric equations, and interpreting discontinuous behavior.

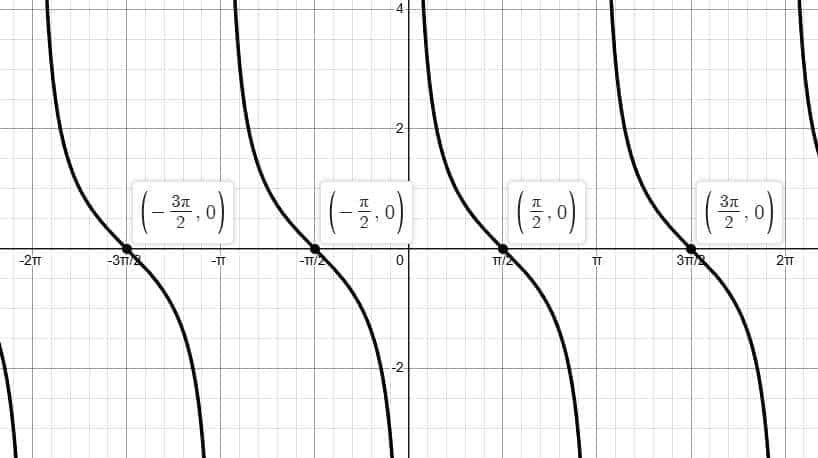
Graph of the Cosecant Function ($\csc x$)

The graph of $\csc x$ is the reciprocal of the sine function and is defined as:

$\csc x = \dfrac{1}{\sin x}$

Because sine becomes zero at certain points, the cosecant graph shows vertical asymptotes and never touches the $x$-axis. It consists of repeating upward and downward curves, making it an important example among the graphs of reciprocal trigonometric functions.

Cosecant is defined as the ratio of the hypotenuse to the opposite side (perpendicular) for a given angle.

Equation of the Cosecant Function

$y = f(x) = \csc x$

In the cosecant graph, angle values are taken along the $x$-axis, and the corresponding values of $y = \csc x$ are plotted on the $y$-axis.

Domain and Range of $\csc x$

Domain of $\csc x$: $x \in \mathbb{R} - \left\{ n\pi \mid n \in \mathbb{Z} \right\}$

The function is not defined where $\sin x = 0$.

Range: $(-\infty, -1] \cup [1, \infty)$

The cosecant function never takes values between $-1$ and $1$.

Period of the Cosecant Function

• Period: $2\pi$

The cosecant graph repeats its pattern after every interval of $2\pi$, just like the sine function.

Vertical Asymptotes of $\csc x$

Vertical asymptotes occur at:

$x = n\pi$, where $n \in \mathbb{Z}$

At these points, $\sin x = 0$, so $\csc x$ becomes undefined.

Amplitude of the Cosecant Function

• Amplitude: Not defined

Since the graph does not have a maximum or minimum value and extends toward $\pm\infty$, amplitude is not defined for $\csc x$.

Symmetry of the Cosecant Graph

Since:

$\csc(-x) = -\csc x$

the cosecant function is an odd function.

Therefore, the graph of $\csc x$ is symmetric about the origin, which helps in sketching and analyzing the graph.

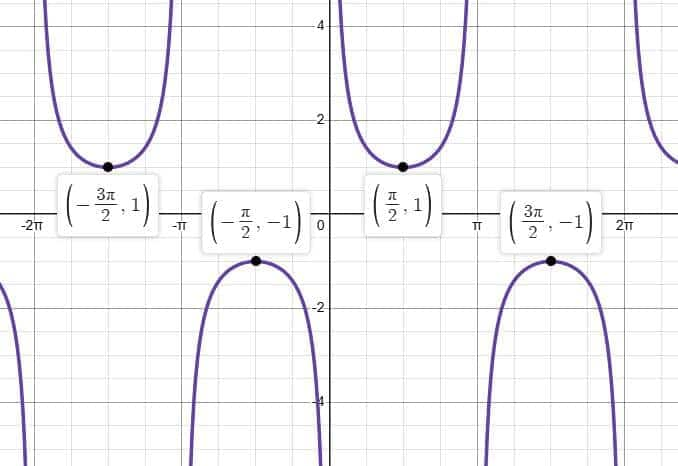
Graph of the Secant Function ($\sec x$)

The graph of $\sec x$ is one of the important reciprocal trigonometric function graphs and is closely related to the graph of $\cos x$. Since secant is the reciprocal of cosine, its graph shows U-shaped curves and vertical asymptotes wherever the cosine function becomes zero. Studying the graph of $\sec x$ helps in understanding inverse wave behavior, undefined values, and discontinuities in trigonometry.

Secant is defined as the ratio of the hypotenuse to the adjacent side (base) for a given angle.

Equation of the Secant Function

$y = f(x) = \sec x$

In the secant graph, angle values are taken on the $x$-axis, and the corresponding values of $y = \sec x$ are plotted on the $y$-axis.

Domain and Range of $\sec x$

Domain: $x \in \mathbb{R} - \left\{ \dfrac{\pi}{2} + n\pi \mid n \in \mathbb{Z} \right\}$

The secant function is not defined where $\cos x = 0$.

• Range:
  $(-\infty, -1] \cup [1, \infty)$

The secant function never takes values between $-1$ and $1$.

Period of the Secant Function

• Period: $2\pi$

The graph of $\sec x$ repeats its shape after every interval of $2\pi$, similar to the cosine function.

Vertical Asymptotes of $\sec x$

Vertical asymptotes occur at:

$x = \dfrac{(2n+1)\pi}{2}$, where $n \in \mathbb{Z}$

At these points, $\cos x = 0$, so $\sec x$ becomes undefined.

Shape and Behaviour of the Secant Graph

Between each pair of vertical asymptotes, the secant graph forms U-shaped curves:

• Opening upward where $\cos x > 0$

• Opening downward where $\cos x < 0$

These curves reflect the reciprocal nature of the cosine function.

Amplitude of the Secant Function

• Amplitude: Not defined

Since the secant graph has no maximum or minimum value and extends toward $\pm\infty$, amplitude is not defined.

Symmetry of the Secant Graph

Since:

$\sec(-x) = \sec x$

the secant function is an even function.

Therefore, the graph of $\sec x$ is symmetric about the $y$-axis, which is useful when sketching and analyzing the graph.

Graph of the Cotangent Function ($\cot x$)

The graph of $\cot x$ is one of the important reciprocal trigonometric function graphs and is closely related to the graph of $\tan x$. Since cotangent is the reciprocal of tangent, its graph shows vertical asymptotes and a decreasing pattern from left to right. Understanding the graph of $\cot x$ helps in visualising decreasing periodic behaviour and discontinuities in trigonometry.

Cotangent is defined as the ratio of the adjacent side (base) to the opposite side (perpendicular) for a given angle.

Equation of the Cotangent Function

$y = f(x) = \cot x$

In the cotangent graph, angle values are taken on the $x$-axis, and the corresponding values of $y = \cot x$ are plotted on the $y$-axis.

Domain and Range of $\cot x$

• Domain: $x \in \mathbb{R} - \left\{ n\pi \mid n \in \mathbb{Z} \right\}$

The function is not defined where $\tan x = 0$.

• Range:
  $\mathbb{R}$

This means the cotangent function can take any real value.

Period of the Cotangent Function

• Period: $\pi$

The cotangent graph repeats itself after every interval of $\pi$, similar to the tangent function.

Vertical Asymptotes of $\cot x$

Vertical asymptotes occur at:

$x = n\pi$, where $n \in \mathbb{Z}$

At these points, $\cot x$ becomes undefined.

Behaviour of the Cotangent Graph

Within each interval, the cotangent function decreases continuously from positive infinity to negative infinity. For example:

$(-2\pi, -\pi)$,
$(-\pi, 0)$,
$(0, \pi)$, and so on.

This decreasing nature distinguishes the cotangent graph from the tangent graph.

Zeros of the Cotangent Function

The roots (zeroes) of $\cot x$ occur at:

$x = \dfrac{n\pi}{2}$, where $n$ is an odd integer

These are the points where the graph crosses the $x$-axis.

Amplitude of the Cotangent Function

• Amplitude: Not defined

Since the cotangent graph extends to $\pm\infty$ and has no maximum or minimum value, amplitude is not defined.

Symmetry of the Cotangent Graph

Since: $\cot(-x) = -\cot x$ the cotangent function is an odd function.

Therefore, the graph of $\cot x$ is symmetric about the origin, which is useful while sketching and analyzing graphs.

Key Features of Trigonometric Graphs

The graphs of trigonometric functions have certain standard features that help us draw, analyze, and interpret them easily. Understanding these features is essential for studying graphs of general trigonometric functions, solving equations, and answering exam-based questions accurately.

Amplitude and Vertical Stretch

Amplitude is the maximum vertical distance of a graph from its baseline (usually the $x$-axis or a shifted midline).

• It shows how tall the peaks and deep the troughs of a wave are

• Applies only to sine and cosine functions

For functions of the form:

$y = a\sin x$ or $y = a\cos x$

• Amplitude $= |a|$

• If $|a| > 1$, the graph stretches vertically

• If $0 < |a| < 1$, the graph compresses vertically

Note: Amplitude is not defined for $\sec x$ and $\csc x$ because these graphs extend to $\pm\infty$ due to asymptotes.

Period and Frequency

The period of a trigonometric function is the horizontal length of one complete cycle.

Standard Periods of Trigonometric Functions

• $\sin x$, $\cos x$, $\sec x$, $\csc x$ → Period $= 2\pi$

• $\tan x$, $\cot x$ → Period $= \pi$

For functions of the form:

$y = \sin(bx)$ or $y = \cos(bx)$

• Period $= \dfrac{2\pi}{|b|}$

Frequency is the number of cycles completed in $2\pi$ units and is the reciprocal of the period.

Phase Shift and Horizontal Shift

A phase shift moves the graph left or right along the $x$-axis.

It appears in functions like:

$y = \sin(bx + c)$ or $y = \cos(bx + c)$

• Phase Shift $= -\dfrac{c}{b}$

• If $c > 0$, the graph shifts left

• If $c < 0$, the graph shifts right

Phase shift changes the starting point of the wave, but not its shape.

Vertical Shift and Baseline Movement

A vertical shift moves the entire graph upward or downward.

It appears in expressions such as:

$y = \sin x + d$ or $y = \cos x + d$

• The new baseline becomes $y = d$

• If $d > 0$, the graph shifts up

• If $d < 0$, the graph shifts down

This changes the midline around which the graph oscillates.

Symmetry of Trigonometric Graphs

Given below is the symmetry of different trigonometric functions:

Even and Odd Functions

• Even functions: $\cos x$, $\sec x$

  • $\cos(-x) = \cos x$

  • Graph is symmetric about the $y$-axis

• Odd functions: $\sin x$, $\tan x$, $\cot x$, $\csc x$

  • $\sin(-x) = -\sin x$

  • Graph is symmetric about the origin

Quadrant-Wise Behaviour of Trigonometric Functions

Based on the ASTC rule:

• First quadrant: All trigonometric functions are positive

• Second quadrant: Sine and cosecant are positive

• Third quadrant: Tangent and cotangent are positive

• Fourth quadrant: Cosine and secant are positive

Understanding this behavior helps in evaluating trigonometric values, sketching graphs, and solving equations.

General Form of Trigonometric Functions

What is the general form of a trigonometric graph? While drawing a graph of the sine function, we convert the given function to the general form as $a \sin (bx – c) + d$ in order to find the different parameters such as amplitude, phase shift, vertical shift and period. Similarly, for the cosine function we can use the formula $a \cos (bx – c) + d$.

The general form of a sine (or cosine) function is:

$y = a \sin(bx + c) + d$

Where:

• $|a|$ is the amplitude , the height of the wave from the midline.

• $\dfrac{2\pi}{|b|}$ is the period , the length of one complete cycle.

• $\dfrac{-c}{b}$ is the phase shift , the horizontal shift of the graph.

• $d$ is the vertical shift , moves the graph up or down, changing the midline to $y = d$.

How to Graph a Trigonometric Function?

To graph a trigonometric function, follow the steps below:

Step 1: Convert the given trigonometric function into its general form:
$y = a \sin(bx + c) + d$

Step 2: Identify the key parameters from the equation:

• Amplitude = $|a|$

• Period = $\dfrac{2\pi}{|b|}$ (for sine and cosine)

• Phase shift = $-\dfrac{c}{b}$

• Vertical shift = $d$

Step 3: Use the appropriate formula for the period:

For sine and cosine: Period = $\dfrac{2\pi}{|b|}$

For tangent and cotangent: Period = $\dfrac{\pi}{|b|}$

Step 4: Plot the graph using the identified parameters. Start by sketching the midline at $y = d$, mark the amplitude above and below the midline, determine the start and end of one period using the phase shift and horizontal stretch, and then plot key points within the cycle to sketch the complete wave.

Transformation of the Graph of Trigonometric Functions

How do transformations affect trig graphs? Let us discuss in depth below:

1. The graph of $y = -f(x)$ from the graph of $y = f(x)$
If $f(x) > 0$, then $-f(x) < 0$, and if $f(x) < 0$, then $-f(x) > 0$.
So, the graph of $y = -f(x)$ is obtained by flipping the graph of $y = f(x)$ vertically (upside down) about the x-axis.
The period of the function does not change in this transformation.
Only the orientation (above/below the x-axis) is reversed.

2. The graph of $y = f(x) + a$ from the graph of $y = f(x)$
The graph of $y = f(x) + a$ is obtained by shifting the graph of $y = f(x)$:

• Upward by $a$ units if $a > 0$

• Downward by $a$ units if $a < 0$

This is a vertical translation.
The shape of the transformed graph remains the same, so the period remains unchanged,
but the range shifts up or down depending on the value of $a$.

3. The graph of $y = f(x - a)$ from the graph of $y = f(x)$
This transformation results in a horizontal shift:

• Shift the graph right by $a$ units if $a > 0$

• Shift the graph left by $a$ units if $a < 0$

This does not affect the amplitude or period, only the starting point of the cycle changes.

4. The graph of $y = a \cdot f(x)$ from the graph of $y = f(x)$
This transformation causes a vertical stretch or compression:

• If $|a| > 1$, the graph is stretched vertically (taller peaks and deeper troughs)

• If $0 < |a| < 1$, the graph is compressed vertically

• If $a < 0$, there is a vertical reflection as well

The amplitude becomes $|a|$ (for sine or cosine).
The period remains unchanged.

5. The graph of $y = f(bx)$ from the graph of $y = f(x)$
This transformation causes a horizontal compression or stretch:

• If $|b| > 1$, the graph is compressed horizontally

• If $0 < |b| < 1$, the graph is stretched horizontally

The new period is:

• For sine and cosine: $\dfrac{2\pi}{|b|}$

• For tangent and cotangent: $\dfrac{\pi}{|b|}$

Shifted Trigonometric Function

A shifted trig function refers to a trigonometric graph that has been moved horizontally or vertically from its standard position. These shifts help model real-world wave patterns and periodic behavior more accurately.

For a general trigonometric function of the form:

$y = a \sin(bx + c) + d \quad \text{or} \quad y = a \cos(bx + c) + d$ the shifts are described as follows:

• Horizontal shift (phase shift): Determined by the value of $c$, and calculated as $\dfrac{-c}{b}$. If $c > 0$, the graph shifts left; if $c < 0$, it shifts right.

• Vertical shift: Controlled by $d$, which moves the graph up if $d > 0$ and down if $d < 0$.

• These modifications result in shifted trig function graphs that maintain the same shape but change position on the coordinate plane.

Understanding how to graph a shifted sine, cosine, or tangent function is crucial when studying the transformation of trig graphs, especially in analysing periodicity of trigonometric functions, amplitude changes, and real-world modelling.

Which Trigonometric Functions have asymptotes?

Trigonometric functions that have asymptotes are those that are undefined at certain points due to division by zero. These include:

• Tangent function ($\tan x$):
  Has vertical asymptotes at
  $x = \dfrac{\pi}{2} + n\pi,\quad n \in \mathbb{Z}$
  because $\tan x = \dfrac{\sin x}{\cos x}$ becomes undefined when $\cos x = 0$.

• Cotangent function ($\cot x$):
  Has vertical asymptotes at
  $x = n\pi,\quad n \in \mathbb{Z}$
  since $\cot x = \dfrac{\cos x}{\sin x}$ becomes undefined when $\sin x = 0$.

• Secant function ($\sec x$):
  Has vertical asymptotes at
  $x = \dfrac{\pi}{2} + n\pi,\quad n \in \mathbb{Z}$
  because $\sec x = \dfrac{1}{\cos x}$ is undefined when $\cos x = 0$.

• Cosecant function ($\csc x$):
  Has vertical asymptotes at
  $x = n\pi,\quad n \in \mathbb{Z}$
  since $\csc x = \dfrac{1}{\sin x}$ is undefined when $\sin x = 0$.

These asymptotes are reflected as vertical lines on the graphs of these functions, indicating points where the function shoots toward positive or negative infinity.

Domain and Range of Trigonometric Functions

Below given are the domain and range of various trigonometric functions such as $\sin x, \cos x$:

Graph Transformations in Trigonometric Functions

Graph transformations in trigonometric functions help us understand how changes in amplitude, period, phase shift, and vertical shift affect the shape and position of sine, cosine, and other trigonometric graphs.

Solved Examples Based on the Graph of Trigonometric Function

Example 1: What is the solution set of the equation $\csc x>1$ in the interval $[0,2 \pi$ ]?

Solution:

Cosecant Function

$y=f(x)=\operatorname{cosec}(x)$

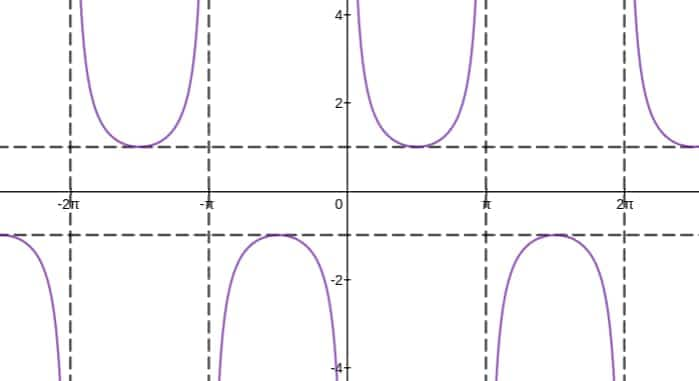
Domain is R - $\{\mathrm{n} \pi, \mathrm{n} \in \mathrm{I}$ (Integers) $\}$
Range is $\mathrm{R}-(-1,1)$
Period is $2 \pi$

As seen in the graph the graph is always on or above the line $x=1$ or below the line $x$ $=-1$

Thus $\operatorname{cosec} \mathrm{x}>1$ will be $x \epsilon[0,2 \pi]-\{\pi / 2,3 \pi / 2\}$ because at $\mathrm{x}=\pi / 2,3 \pi / 2$; $\operatorname{cosec} x=1$

Example 2: What is the range of $f(x)=\sin|3x^3| \ \ x\epsilon R$?

Solution: Graph of sine function

y = f(x) = sin(x)

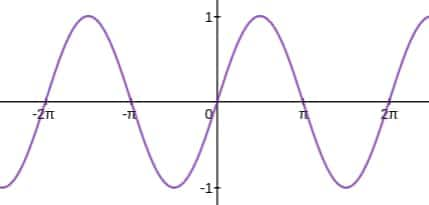
Now,

$f(x)=\sin \left|3 x^3\right|, \quad x \in R$

$\text { assume }\left|3 x^3\right|=t, \quad t \geq 0$
Now, from graph if $t \geq 0$, then $y=\sin (t)$ takes all values in $[-1,1]$ So, range is $[-1,1]$.

Example 3: The number of solutions of $\sin 3x = \cos 2x$, in the interval $\left(\frac{\pi}{2}, \pi\right)$ is: [JEE MAINS 2018]

Solution: We are given the equation: $\sin 3x = \cos 2x$

Using the identity: $\cos \theta = \sin\left(\frac{\pi}{2} - \theta\right)$

We rewrite the equation as: $\sin 3x = \sin\left(\frac{\pi}{2} - 2x\right)$

Now using the identity: If $\sin A = \sin B$, then
$A = B + 2n\pi$ or $A = \pi - B + 2n\pi$

Case 1: $3x = \frac{\pi}{2} - 2x + 2n\pi$
$\Rightarrow 5x = \frac{\pi}{2} + 2n\pi$
$\Rightarrow x = \frac{\pi + 4n\pi}{10}$

Case 2: $3x = \pi - \left(\frac{\pi}{2} - 2x\right) + 2n\pi$
$\Rightarrow 3x = \frac{\pi}{2} + 2x + 2n\pi$
$\Rightarrow x = \frac{\pi}{2} + 2n\pi$

Now find values of $x$ in the interval $\left(\frac{\pi}{2}, \pi\right)$

From Case 1: $x = \frac{(1 + 4n)\pi}{10}$

Try $n = 1$: $x = \frac{5\pi}{10} = \frac{\pi}{2}$ excluded
Try $n = 2$: $x = \frac{9\pi}{10} \in \left(\frac{\pi}{2}, \pi\right)$
Try $n = 3$: $x = \frac{13\pi}{10} > \pi$ not allowed

From Case 2: $x = \frac{\pi}{2} + 2n\pi$ all values exceed $\pi$ in the interval

So, only one solution exists.

Hence, the number of solutions is $1$.

Example 4: If $f(x)= 4\cos\theta+\sin^2\theta$ Which of the following is true for f(x)?

a) At $\theta=0$ $f(x)$ has its maximum value and maximum value of $f(x)$ is $5$

b) At $\theta=\pi$ $f(x)$ has its minimum and minimum value of $f(x)$ is $-5$

c) At $\theta=\pi$ $f(x)$ has its minimum value and minimum value of $f(x)$ is -4

d) At $\theta=0$ $f(x)$ has its minimum value and minimum value of $f(x)$ is 1

Solution: Cosine Function

y = f(x)= cos(x)

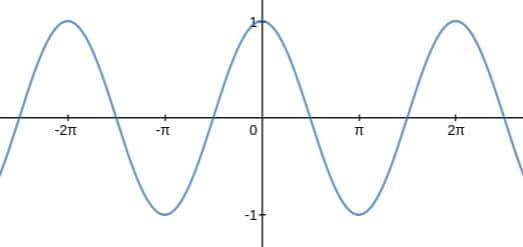
Domain is R

Range is [-1, 1]

$\begin{aligned} & f(x)=4 \cos \theta+\sin ^2 \theta \\ = & 4 \cos \theta+1-\cos ^2 \theta \\ = & 5-\left(\cos ^2-4 \cos \theta+4\right) \\ = & 5-(\cos \theta-2)^2\end{aligned}$

minimum value of f(x) at $\theta=\pi$

f(x)min=$5-9=-4$

maximum value of$ f(x)$ at $\theta=0$

f(x)max=5-1=4

Hence, the correct answer is the option (3).

Example 5: Find out the range of the function $f(x)=\sqrt{9+\sqrt{\left(1+\cot ^2 x\right)}}, x \in\{R-\{n \pi, n \epsilon$ Integers $\}\}$.

Solution: $f(x)=\sqrt{9+\sqrt{\left(1+\cot ^2 x\right)}}$

$=\sqrt{9+\sqrt{\left(\csc ^2 x\right)}}$

$=\sqrt{9+|\csc (x)|}$

$\text { Range of } \csc (x) \text { is }(-\infty,-1] \cup[1, \infty)$

$\text { So, }|\csc (x)| \geq 1$

$f(x) \geq \sqrt{10}$

$f(x) \epsilon[\sqrt{10}, \infty)$

List of Topics Related to the Trigonometric Functions

Trigonometric functions form the foundation of many concepts in mathematics and physics. This section provides a comprehensive list of key topics,including identities, transformations, inverse functions, and applications,that are essential for mastering the subject and excelling in competitive exams.

NCERT Resources

Mastering Trigonometric Functions from NCERT Class 11 Chapter 3 is key to understanding the graphs of trigonometric functions, identities, and formulas. This section includes structured notes, solved examples, and practice problems on the graph of sin(x), cos(x), tan(x), amplitude and phase shift in trigonometry, and the periodicity of trigonometric functions,all aligned with the latest syllabus for CBSE and competitive exams.

NCERT Class 11 Chapter 3 Trigonometric Functions Notes

NCERT Class 11 Chapter 3 Trigonometric Functions Solutions

NCERT Exemplar Class 11 Chapter 3 Trigonometric Functions

Practice Questions on Graphs of Trigonometric Functions

These practice questions focus on the graphs of trigonometric functions, including the sine, cosine, tangent graph and the graphs of sec, cosec, and cot functions. You'll explore the general form of trigonometric functions, amplitude and phase shift in trigonometry, and the periodicity of trigonometric functions. Learn how to draw trigonometric graphs and understand how transformations affect trig graphs, especially in shifted trig function graphs.

Graphs Of General Trigonometric Functions - Practice Now

We have provided the list of practice questions based on the following topics: