Bohrs Model - History, Structure, Theories, Limitations, FAQs

Bohr's model of the atom was originally proposed by Neil Bohr in 1915. And further modified by Rutherford. The Rutherford model introduces the nuclear atom model, in which he explains that poorly charged electrons surround the nucleus (well-charged). The Bohr model consists of a small (well-charged) nucleus surrounded by negative electrons moving around the nucleus in pathways. Bohr found that electrons located far from the nucleus are more powerful, and electrons close to the nucleus are less powerful.

This Story also Contains

1. Postulates of Bohr Model Atom
2. Limitations of Bohr Model Atom
3. History of the Bohr Model
4. Modified Bohr Model
5. Sommerfeld atomic model

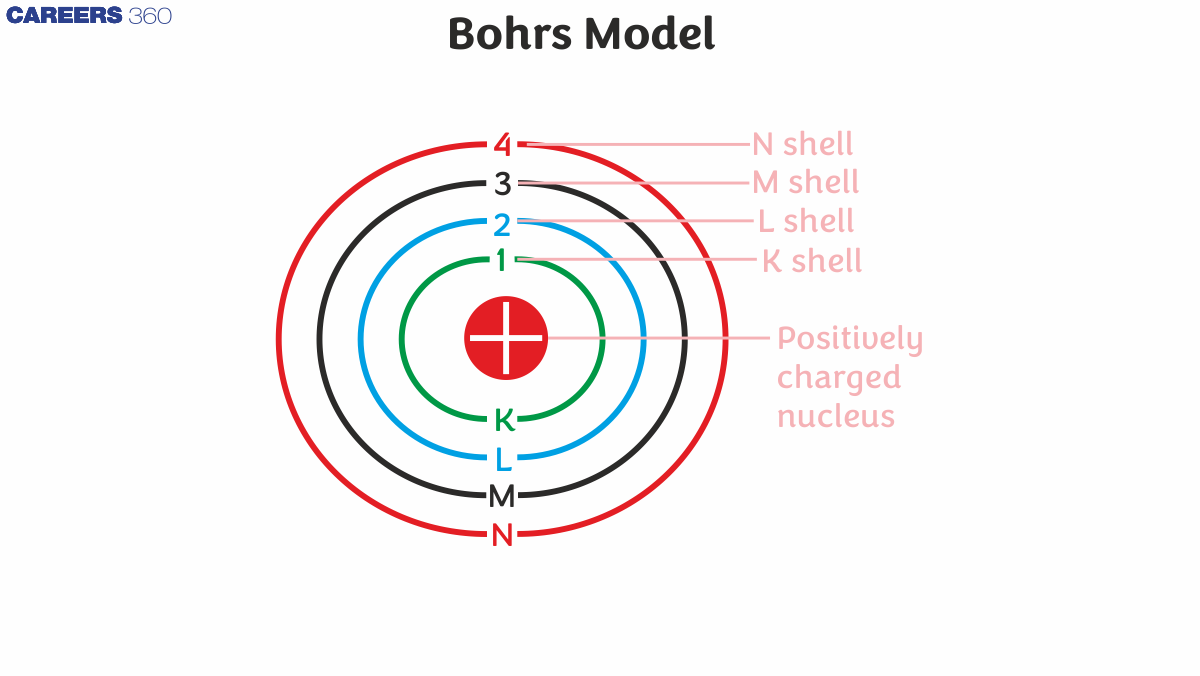
Postulates of Bohr Model Atom

In an atom, electrons (badly charged) revolve around a well-charged nucleus in a clear circular pattern called orbits or shells.

Each circle or shell has a fixed force and these circular lines are known as orbital shells.

Power levels are represented by a whole number (n = 1, 2, 3…) known as a quantum number.

This quantum numerical range starts from the side of the nucleus with n = 1 having the lowest energy level.

Orbits n = 1, 2, 3, 4, and so on... are assigned as K, L, M, N, and so on… shells, and when the electron reaches a very low level of energy, it is said to be in the ground state.

Electrons in the atom go from low energy to high energy by getting the energy needed and electrons move from high energy to high energy levels by losing energy.

Limitations of Bohr Model Atom

Bohr's atomic model failed to explain the effect of Zeeman (the effect of magnetic force on a series of atoms).

It also failed to explain the effect of Stark (the effect of the electric field on the atomic spectrum).

It violates the Heisenberg Uncertainty Principle rule.

Could not define spectra obtained from large atoms.

Also read :

History of the Bohr Model

The discovery of electrons and radioactivity in the late 19th century led to a variety of proposed atomic formations.

In 1913, Niels Bohr proposed the idea of a hydrogen atom, based on the quantum assumption that a certain body part takes only different amounts. Electrons revolve around the nucleus, but only in fixed lines, and When electrons cross the low-energy path, the difference is sent as radiation. Bohr's model explained why atoms only emit light at fixed wavelengths, and later inject ideas into light quanta.

Modified Bohr Model

Despite the success of the Bohr model, there have been major flaws. On the test side, a detailed analysis of hydrogen extraction found a single extraction line actually consisting of two or more closely spaced lines, a feature not found in the Bohr model. Theoretically, the Bohr model mixes particle images with electron waves, which were considered by many to be unsatisfactory.

For these reasons, better treatment of hydrogen atoms was bought when the electron was considered a wave from the beginning. This theory, developed by Heisenberg, Pauli, Schrödinger, Sommerfeld, and others, is well mathematically accurate. The main result from this theory is that four Quantum Numbers describe the state of the electron, compared to the single quantum n number present in the Bohr model. These quantum numbers are as follows:

n, the principle quantum number. This is similar to the Bohr type, and can take up values of 1,2,3, ....

l, orbital quantum number. This is a label that describes the magnitude of the angular pressure of an electron. With a given n, l can take values 0,1,2, ..., n - 1.

ml, the number of spin-orbital quantum. This is a label that describes the angular component of an electron vector. For a given l, ml can take values - l, - l + 1, ..., - 1,0,1, ..., l - 1, l.

ms, the quantum spin number. This label, in a very limited sense, can be regarded as setting a point where an electron rotates on its axis. ms can take one of two values, $ \ pm $ 1/2.

Therefore, for a given n, there may be 2n 2 areas with different values of l, ml, and ms.

Historically, the primary quantum n label is called a Shell, and n = 1,2,3, ... the shell is sometimes called the K, L, M, ... shell.

The number of orbital quantum l labels subshells, and l = 0,1,2,3,4, ... the subshell is also called s, p, d, f, ... subshell.

If we consider starting electrons to form different atoms, then one would expect all the electrons to enter the lowest energy state, namely n = 1 and l = 0 = ml. This does not happen in nature, however. Paul explained this by posting that the electrons adhere to what is now called the Pauli emission system:

No two electrons in a system can have the same sets of quantum numbers.

Sommerfeld atomic model

To explain the fine structure of spectral lines, Sommerfeld introduced two major changes in Bohr's thinking.

(i) According to Sommerfeld, the electron path around the nucleus is, in general, a circle with a nucleus in one of its foci.

(ii) The electron velocity of an elliptical orbit varies with different parts of the orbit. This results in variations in the intensity of the moving electron.

Now, when elliptical lines are allowed, one has to deal with a wide variety of variations.

(i) Different electron distance from the nucleus (r).

(ii) Different angular position of the electron in relation to the nucleus eg azimuthal angle φ

To address these two changes, two quantum numbers are introduced

(i) A large quantum n quantum n theory of Bohr, which determines electron energy, and

(ii) a new quantum number called the orbital (or azimuthal) quantum number (l) introduced to match the angular force in an orbit e.g., determines the orbital angular force of the electron. Its values vary from zero to (n-1) in the singular steps.

This quantum orbital number (l) assists in locating elliptical orbits. Possible elliptical lines are that of

b / a = l + 1 / n

when a and b are large and small axes in the order of the ellipse.

According to Sommerfeld's model, in any of the quantum n numbers, there are possible variations in the so called sub sub-shells. With the exception of subshells, one is round and the remainder (i.e., n-1) has an elliptical shape.

The lower extremities have slightly different strengths due to differences in electron mass density.

Consider the initial energy level (n = 1). When n = 1, l = 0 that is, at this energy level, there is only one orbital or subshell of the electron. Also, when a = b, two ellipse axes are equal. As a result, the orbit corresponding n = 1 is a circle. This subscription is selected as a sub-shell. As, the bottom shell belongs to n = 1, it is called 1s

Similarly, at the second level of energy n = 2, there are two electrons allowed. At n = 2, l can take two values, 0 and 1.

When n = 2, l = 0.

b / a = 0 + 1/2 = 1/2

or

b = a / 2

This text corresponding to l = 0 is elliptical in shape and is set as 2s.

where n = 2, l = 1.

b / a = 1 + 1/2 = 2/2 = 1

or

b = a

This subshell corresponding to l = 1 is circular and is shaped like 2p (Fig. B).

At n = 3, l has three numbers 0, 1 and 2, i.e. there are three electrons allowed in the electrons.

where n = 3, l = 0.

b / a = (0 + 1) / 3 = 1/3 = 1 or b = a / 3

where, n = 3, l = 1.

b / a = (1 + 1) / 3 = 2/3 = 1 or b = 2a / 3

and when n = 3, l = 2.

b / a = (2 + 1) / 3 = 3/3 = 1 or b = a

The lower shells corresponding to l = 0, 1, and 2 are designated as 3s, 3p and 3d respectively. The round shell is classified as 3d and the other two are elliptical.

It is a common practice to assign letters to l values as given below:

Orbital quantum number l - 0,1,2,3,4.

Electron state: s, p,d,f,g.

Therefore, the electrons in the earth l = 0, 1, 2, 3 are said to be in the areas of s, p, d, and f-states.

Beautiful structure of the spectral line

According to the Sommerfeld atomic model, the absolute electron energy in an elliptical orbit can be expressed as,

En = (-me4Z2) / (8ε02h2n2)

This statement is similar to the one received by Bohr. The introduction of elliptical lines therefore does not provide new levels of energy and therefore no new changes.

In such a way, Sommerfeld's attempt to explain the fine structure of the spectral lines failed.

But soon, on the basis of the electron density variation in speed, Sommerfeld could find a solution to the problem of a fine spectral line structure.

According to Sommerfeld, the electron velocity is highest when the electron is closest to the nucleus and smaller when it is farther away from the nucleus because the electron path is circular. This means that the active weight of an electron will vary in different parts of its cycle. Recalling the differences in electron density,

Sommerfeld corrected his theory and showed that the electron path is not a simple ellipse but a precursor circle called a rosette

Also read -