Application of Integrals

Let's consider a garden. If you wish to find the area of a specific place inbetween the flowerbed to make a pathway, all you need is integrals. The area for the pathway can be easily found with the help of integrals using the formula of area between curves.

This article is about the concept of class 12 maths Application of Integrals. Application of Integrals chapter is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, VITEEE, BCECE, and more.

Application of Integrals

One of the important application of integrals is finding the area bounded by two or more curves. The application of integrals by finding area bounded by curves is also used in economics to find the total revenue and cost over time, physics to find the work done by a force over a distance, etc.

Before looking into this applicatio of integrals, let us recall what is integrals.

Integrals

Integration is the reverse process of differentiation. In integration, we find the function whose differential coefficient is given.

Integrals are based on a limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs.

For example,

$\begin{aligned} & \frac{d}{d x}(\sin x)=\cos x \\ & \frac{d}{d x}\left(x^2\right)=2 x \\ & \frac{d}{d x}\left(e^x\right)=e^x\end{aligned}$

In the above example, the function $\cos (x)$ is the derivative of $\sin (x)$. We say that $\sin (x)$ is an antiderivative (or an integral) of $\cos (x)$. Similarly, $x^2$ and $e^x$ are the antiderivatives (or integrals) of $2 x$ and $\mathrm{e}^{\mathrm{x}}$ respectively.

Also note that the derivative of a constant (C) is zero. So we can write the above examples as:

$\begin{aligned}
& \frac{d}{d x}(\sin x+c)=\cos x \\
& \frac{d}{d x}\left(x^2+c\right)=2 x \\
& \frac{d}{d x}\left(e^x+c\right)=e^x
\end{aligned}$

Thus, the anti-derivatives (or integrals) of the above functions are not unique. There exist infinitely many anti-derivatives of each of these functions which can be obtained by selecting C arbitrarily from the set of real numbers.

Some basic integrals formulas

1. $\int 0 d x=c$, where $c$ is a constant

2. $\int k d x=k x+c$ where $c$ is a constant

3. $\int x^n d x=\frac{x^{n+1}}{n+1}+c, \quad n \neq-1$ (Power rule)

4. $\int \frac{1}{x} d x=\log |x|+c$

5. $\int \sin x d x=-\cos x+c$

6. $\int \cos x d x=\sin x+c$

7. $\int \sec ^2 x d x=\tan x+c$

8. $\int \operatorname{cosec}^2 x d x=-\cot x+c$

9. $\int \sec x \tan x d x=\sec x+c \\$

10. $\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+c $

11. $\int e^x d x=e^x+c$

12. $\int a^x d x=\frac{a^x}{\log a}+c$

13. $\int \frac{1}{\sqrt{1-x^2}} d x=\sin ^{-1} x+c$

14. $\int \frac{1}{1+x^2} d x=\tan ^{-1} x+c$

Application of Integrals Class 12 Notes

The application of Integrals class 12 notes includes - the area along the X-axis and Y-axis, the area of piecewise function and the area bounded by two curves.

Area along X-axis

If the function $f(x) ≥ 0 ∀ x ∈ [a, b]$ then $\int_a^{\infty} f(x) d x$ represents the area bounded by $y = f(x), x-$axis and lines $x = a$ and $x = b$.

If the function $f(x) ≤ 0 ∀ x ∈ [a, b]$, then the area by bounded $4y = f(x)$, x-axis and lines $4x = a$ and $x = b$ is $\int_a^b f(x) d x$.

Area along Y-axis

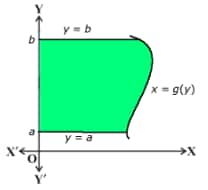
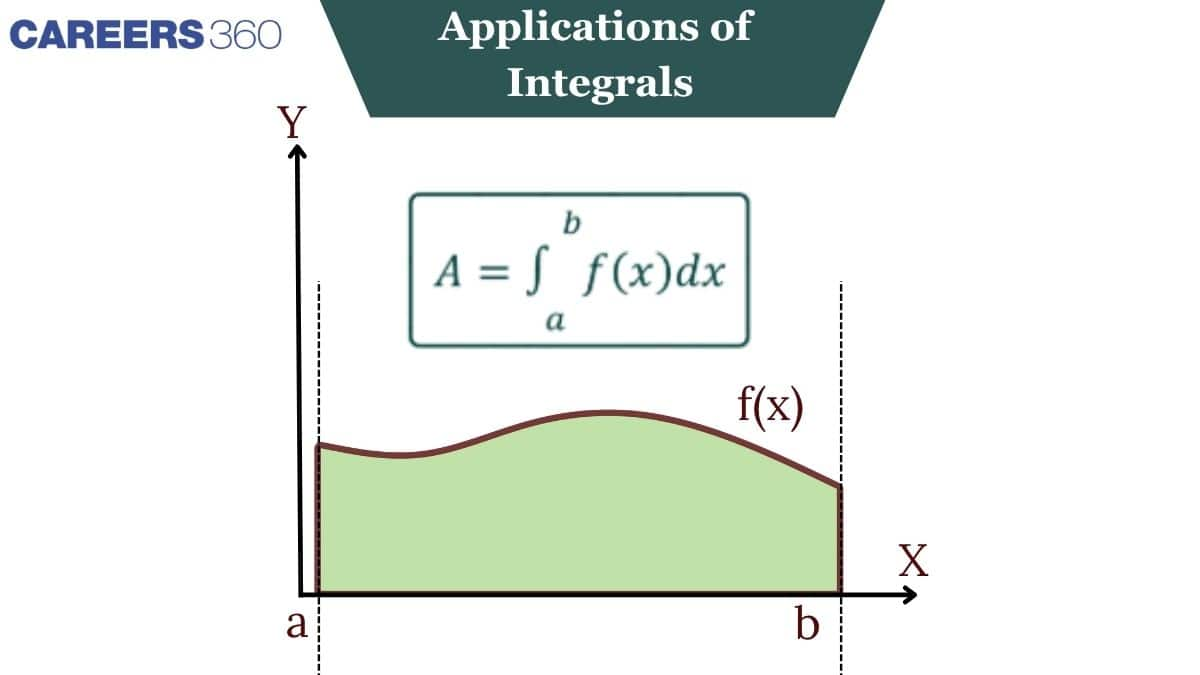
The area by bounded $x = g(y)$ [with $g(y)>0$], $y$-axis and the lines $y = a$ and $y = b$ is $\int_a^b x d y=\int_a^b g(y) d y$

Area of Piecewise Function

If the graph of the function $f(x)$ is of the following form, then

then $\int_a^b f(x) d x$ will equal $A_1-A_2+A_3-A_4$ and not $A_1+A_2+A_3+A_4$.

If we need to evaluate $A_1+A_2+A_3+A_1$ (the magnitude of the bounded area) we will have to calculate

$ \underbrace{\int_a^x f(x) d x}_{\mathrm{A}_1}+\underbrace{\left|\int_x^y f(x) d x\right|}_{\mathrm{A}_2}+\underbrace{\int_5^z f(x) d x}_{\mathrm{A}_3}+\underbrace{\left|\int_z^b f(x) d x\right|}_{\mathrm{A}_4} $

The area bounded by the curve when the curve intersects $X$-axis

The graph $y=f(x) \forall x \in[a, b]$ intersects $x-a x i s$ at $x=c$.

If the function $f(x) \geq 0 \forall x \in[a, c]$ and $f(x) \leq 0 \forall x \in[c, b]$ then area bounded by curve and $x$-axis, between lines $x=a$ and $x=b$ is

$ \int_a^b|f(x)| d x=\int_a^c f(x) d x-\int_c^b f(x) d x$

Area Bounded by Two Curves

Area bounded by the curves $y=f(x), y=g(x) $ and the lines $ x = a$ and $x = b$, and it is given that $f(x) ≤ g(x). $

From the figure, it is clear that,

Area of the shaded region = Area of the region $ABEF$ - Area of the region $ABCD$

$\int_a^b g(x) d x-\int_a^b f(x) d x=\int_a^b(\underbrace{g(x)}_{\begin{array}{c}\text { upper } \\ \text { curve }\end{array}}-\underbrace{f(x)}_{\begin{array}{c}\text { lower } \\ \text { curve }\end{array}}) d x$

Area Bounded by Curves When Intersects at More Than One Point

Area bounded by the curves $y = f(x), y = g(x)$ which intersect each other in the interval $[a, b]$

First find the point of intersection of these curves $y = f(x)$ and $y = g(x)$ by solving the equation $f(x) = g(x)$, let the point of intersection be $x = c $

$=\int_a^c\{f(x)-g(x)\} d x+\int_c^b\{g(x)-f(x)\} d x$

When two curves intersects more than one point

Area bounded by the curves $y=f(x), y=g(x)$ which intersect each other at three points at $x = a, x = b$ and $x = c. $

To find the point of intersection, solve $f(x) = g(x). $

For $x ∈ (a, c), f(x) > g(x)$ and for $x ∈ (c, b),g(x) > f(x).$

Area bounded by curves,

$\begin{aligned} A & =\int_a^b|f(x)-g(x)| d x \\ & =\int_a^c(f(x)-g(x)) d x+\int^b(g(x)-f(x)) d x\end{aligned}$

Now, let us summarize and recall the application of integrals class 12 formulas.

Application of Integrals Formula

Application of integrals class 12 formulas include the formulas for the topics area along the X-axis and Y-axis, area of piecewise function, and are bounded by two curves.

Area along X-axis

If the function $f(x) ≥ 0 ∀ x ∈ [a, b]$ then $\int_a^{\infty} f(x) d x$ represents the area bounded by $y = f(x), x-$axis and lines $x = a$ and $x = b$.

If the function $f(x) ≤ 0 ∀ x ∈ [a, b]$, then the area by bounded $4y = f(x)$, x-axis and lines $4x = a$ and $x = b$ is $\int_a^b f(x) d x$.

Area along Y-axis

The area by bounded $x = g(y)$ [with $g(y)>0$], $y$-axis and the lines $y = a$ and $y = b$ is $\int_a^b x d y=\int_a^b g(y) d y$

Area of Piecewise Function

If the function $f(x) \geq 0 \forall x \in[a, c]$ and $f(x) \leq 0 \forall x \in[c, b]$ then area bounded by curve and $x$-axis, between lines $x=a$ and $x=b$ is

$ \int_a^b|f(x)| d x=\int_a^c f(x) d x-\int_c^b f(x) d x$

Area Bounded by Two Curves

Area bounded by the curves $y=f(x), y=g(x) $ and the lines $ x = a$ and $x = b$, and it is given that $f(x) ≤ g(x). $

Area bounded by the curves = $\int_a^b g(x) d x-\int_a^b f(x) d x=\int_a^b(\underbrace{g(x)}_{\begin{array}{c}\text { upper } \\ \text { curve }\end{array}}-\underbrace{f(x)}_{\begin{array}{c}\text { lower } \\ \text { curve }\end{array}}) d x$

Applications of Integrals Class 12

Now, let us look into some other application of integrals class 12.

• Integrals are used to form images which has greater applications in technology. This is one of the important applications which helps in the field of medicine through CT and MRI scans.
• In the topic of probability, the integrals are in the concept of probability density function(PDF).

Importance of Class 12 Application of Integrals

Application of integrals have a significant weighting in the IIT JEE test, which is a national level exam for 12th grade students that aids in admission to the country's top engineering universities. It is one of the most difficult exams in the country, and it has a significant impact on students' futures. Several students begin studying as early as Class 11 in order to pass this test. When it comes to math, the significance of these chapters cannot be overstated due to their great weightage. You may begin and continue your studies with the standard books and these revision notes, which will ensure that you do not miss any crucial ideas and can be used to revise before any test or actual examination.

How to Study Class 12 Application of Integrals?

Start preparing by understanding and practicing the concept of integrals. Try to be clear on applicatio of integrals formula of are of curves at dirfferent cases. . Practice many problems from each topic for better understanding. Remember to revise the application of integrals formulas again and again.

If you are preparing for competitive exams then solve as many problems as you can. Do not jump on the solution right away. Remember if your basics are clear you should be able to solve any question on this topic.

NCERT Notes Subject wise link:

• NCERT Notes for class 12 Physics.
• NCERT Notes for class 12 Chemistry.
• NCERT Notes for class 12 Mathematics.
• NCERT Notes for class 12 Biology

Important Books for Class 12 Application of Integrals

Start from NCERT Books, the illustration is simple and lucid. You should be able to understand most of the things. Solve all problems (including miscellaneous problem) of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the book Amit M Aggarwal's differential and integral calculus or Cengage Algebra Textbook by G. Tewani but make sure you follow any one of these not all. Applications of integrals are explained very well in these books and there are an ample amount of questions with crystal clear concepts. Choice of reference book depends on person to person, find the book that best suits you the best, depending on how well you are clear with the concepts and the difficulty of the questions you require.

NCERT Solutions Subject wise link:

• NCERT solutions for class 12 Physics.
• NCERT solutions for class 12 Chemistry.
• NCERT solutions for class 12 Mathematics.
• NCERT solutions for class 12 Biology.

NCERT Exemplar Solutions Subject wise link:

• NCERT exemplar solutions for class 12 Physics.
• NCERT exemplar solutions for class 12 Chemistry.
• NCERT exemplar solutions for class 12 Mathematics.
• NCERT exemplar solutions for class 12 Biology.