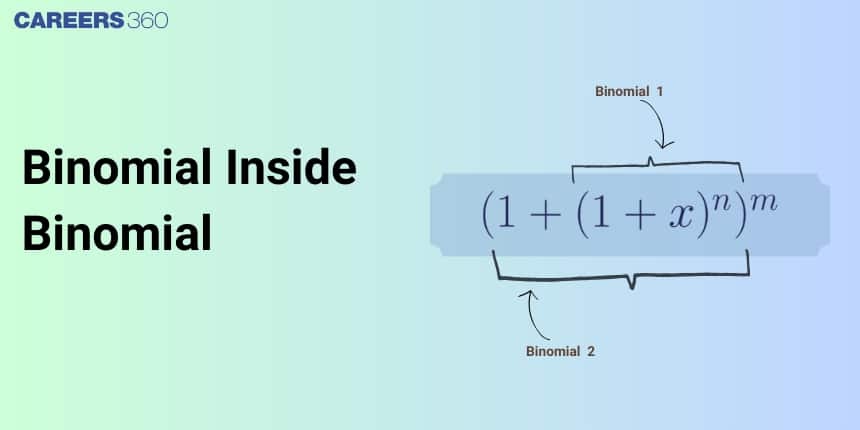
Binomial inside Binomial

An expression with two terms is called the binomial expansion. In the case of higher degree expression, it is difficult to calculate it manually. In these cases, Binomial theorem can be used to calculate it. Binomial theorem is used for the expansion of a binomial expression with a higher degree. Binomial coefficients are the coefficients of the terms in the Binomial expansion. Binomial theorem is proved using the concept of mathematical induction. Apart from Mathematics, Binomial theorem is also used in statistical and financial data analysis.

This article is about the binomial inside binomial which falls under the broader category of Binomial Theorem and its applications. It is one of the important topics for competitive exams.

Binomial Theorem

Statement:

If $n$ is any positive integer, then

$ (a + b)^n = \binom{n}{0} a^n + \binom{n}{1} a^{n - 1} b + \binom{n}{2} a^{n - 2} b^2 + \dots + \binom{n}{n - 1} a b^{n - 1} + \binom{n}{n} b^n $

Proof:

The proof is obtained by applying the principle of mathematical induction.

Let the given statement be:

$ P(n): (a + b)^n = \binom{n}{0} a^n + \binom{n}{1} a^{n-1} b + \binom{n}{2} a^{n-2} b^2 + \dots + \binom{n}{n-1} a b^{n-1} + \binom{n}{n} b^n $

For $ n = 1 $, we have:

$ P(1): (a + b)^1 = \binom{1}{0} a^1 + \binom{1}{1} b^1 = a + b $

Thus, $ P(1) $ is true.

Suppose $ P(k) $ is true for some positive integer $ k $, i.e.,

$ (a + b)^k = \binom{k}{0} a^k + \binom{k}{1} a^{k-1} b + \binom{k}{2} a^{k-2} b^2 + \dots + \binom{k}{k} b^k$

We shall prove that $ P(k + 1) $ is also true, i.e.,

$ (a + b)^{k + 1} = \binom{k+1}{0} a^{k+1} + \binom{k+1}{1} a^k b + \binom{k+1}{2} a^{k-1} b^2 + \dots + \binom{k+1}{k+1} b^{k+1} $

Now,

$ (a + b)^{k + 1} = (a + b)(a + b)^k $

$ = (a + b) \left[\binom{k}{0} a^k + \binom{k}{1} a^{k-1} b + \binom{k}{2} a^{k-2} b^2 + \dots + \binom{k}{k-1} a b^{k-1} + \binom{k}{k} b^k\right] $

[from (1)]

$ = \binom{k}{0} a^{k+1} + \binom{k}{1} a^k b + \binom{k}{2} a^{k-1} b^2 + \dots + \binom{k}{k-1} a^2 b^{k-1} + \binom{k}{k} a b^k $

$ + \binom{k}{0} a^k b + \binom{k}{1} a^{k-1} b^2 + \binom{k}{2} a^{k-2} b^3 + \dots + \binom{k}{k-1} a b^k + \binom{k}{k} b^{k+1} $

[by actual multiplication]

$ = \binom{k}{0} a^{k+1} + (\binom{k}{1} + \binom{k}{0}) a^k b + (\binom{k}{2} + \binom{k}{1}) a^{k-1} b^2 + \dots + (\binom{k}{k} + \binom{k}{k-1}) a b^k + \binom{k}{k} b^{k+1} $

[grouping like terms]

$ = \binom{k+1}{0} a^{k+1} + \binom{k+1}{1} a^k b + \binom{k+1}{2} a^{k-1} b^2 + \dots + \binom{k+1}{k} a b^k + \binom{k+1}{k+1} b^{k+1}$

(by using $ \binom{k+1}{0} = 1 $, $ \binom{k}{r} + \binom{k}{r-1} = \binom{k+1}{r} $, and $ \binom{k}{k} = 1 = \binom{k+1}{k+1} $)

Thus, it has been proved that $ P(k + 1) $ is true whenever $ P(k) $ is true. Therefore, by the principle of mathematical induction, $ P(n) $ is true for every positive integer $ n $.

Binomial Coefficient

The combination $\binom{n}{r}$ or ${ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}$ occuring in the Binomial theorem is called a Binomial coefficient, where $\binom{n}{r}=C(n, r)={ }^n C_r=\frac{n!}{r!(n-r)!}$.

Binomial inside Binomial

Let's see some examples to understand about combining binomials.

How do we find the summation of the series where upper index also varies e.g., $\sum_{r=0}^n{ }^{n+r} C_r={ }^n C_0+{ }^{n+1} C_1+{ }^{n+2} C_2+\cdots+{ }^{n+n} C_n$

[put value of $r=0,1,2, \ldots \ldots$, upto n]

By using the property of the binomial coefficient

$ { }^n C_r={ }^n C_{n-r} $

$\sum_{r^n=0}^{\mathrm{n}+{ }^{\mathrm{r}}} \mathrm{C}_{\mathrm{r}}={ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}}+{ }^{\mathrm{n}+1} \mathrm{C}_{\mathrm{n}}+{ }^{\mathrm{n}+2} \mathrm{C}_{\mathrm{n}}+\cdots+{ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{n}} $

$\text { Now as }{ }^{\mathrm{n}} C_n={ }^{n+1} C_{n+1}=1 \text {, so we can write } $

$\sum_{\mathrm{r}=0}^{\mathrm{n}}{ }^{\mathrm{n}+\mathrm{r}} \mathrm{C}_{\mathrm{r}}={ }^{\mathrm{n}+1} \mathrm{C}_{\mathrm{n}+1}+{ }^{\mathrm{n}+1} \mathrm{C}_{\mathrm{n}}+{ }^{\mathrm{n}+2} \mathrm{C}_{\mathrm{n}}+\cdots+{ }^{2 \mathrm{n}} \mathrm{C}_{\mathrm{n}} $

Now first $2$ terms can be combined by using the property

${ }^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r $

$\sum_{r=0}^{\mathrm{n}}{ }^{\mathrm{n}+\mathrm{r}} C_r={ }^{\mathrm{n}+2} C_{\mathrm{n}+1}+{ }^{\mathrm{n}+2} C_n+\cdots+{ }^{2 n} C_n $

now first two terms can again be combined using the same property, and this process can be continued till last term is also combined

$ ={ }^{2 n+1} C_{n+1} $

Solved Examples Based on Binomial inside Binomial

Example 1: If $(1+x)^n=C_0+C_1 x \ldots \ldots+C_n x^n$, then

$C_0{ }^{2 n} C_n-C_1 \cdot{ }^{2 n-1} C_n+C_2 \cdot{ }^{2 n-2} C_n-C_3 \cdot{ }^{2 n-3} C_n+\ldots+(-1)^n C_n \cdot{ }^n C_n $ is equal to

1) $\frac{1}{n}$

2) $2^{-n}$

3) $2^n$

4) $1 $

Solution:

Binomial Inside Binomial

$C_0 \cdot{ }^{2 n} C_n-C_1 \cdot{ }^{2 n-1} C_n+C_2 \cdot{ }^{2 n-2} C_n-C_3 \cdot{ }^{2 n-3} C_n+\ldots+(-1)^n C_n \cdot{ }^n C_n $

$=\text { Coefficient of }{\underset{\sim}{x}}^n \text { in } $

${\left[C_0(1+x)^{2 n}-C_1(1+x)^{2 n-1}+C_2(1+x)^{2 n-2}\right.} $

$\left.\quad-C_3(1+x)^{2 n-3}+\ldots+(-1)^n{ }^n C_n \cdot(1+x)^n\right] $

Coefficient of $x_n$ in

$ (1+x)^n\left[C_0(1+x)^n-C_1(1+x)^{n-1}+C_2(1+x)^{n-2}\right. $

$\left.-C_3(1+x)^{n-3}+\ldots+(-1)^n \cdot{ }^n C_n \cdot 1\right] $

$=\text { Coefficient of }{\underset{\sim}{n}}^n \text { in }(1+x)^n\left[((1+x)-1)^n\right] $

$=\text { Coefficient of }{\underset{\sim}{\mathrm{X}}}_{\mathrm{n}} \text { in }(1+x)^n \cdot x^n $

$=\text { Constant term in }(1+x)^n=1 $

Hence, the answer is option 4.

Example 2: In a hockey series between teams $X$ and $Y$, they decide to play till a team wins ' $m$ ' matches. Then the number of ways in which team $X$ wins is

1) $2^m$

2) ${ }^{2 m} P_m$

3) ${ }^{2 m} C_m$

4) None of these

Solution:

Theorem of Combination-

Each of the different groups or selections which can be made by taking r things from $n$ things is called a combination.

$ { }^n c_r=\frac{(n)!}{r!(n-r)!} $

wherein

Where $1 \leq r \leq n$

Team X will win if it wins $(m+r)$ th match and

wins $m-1$ match from the first $m+r-1$ matches,

Thus, the total number of ways $=\sum_{r=0}^m{ }^{m+r-1} C_{m-1}=\frac{{ }^{2 m} C_m}{2}$

Hence, the answer is option 4.

Example 3: The sum $S_n=\sum_{k=0}^n(-1)^k \cdot{ }^{3 n} C_k$ where $\mathrm{n}=1,2$, is

1) $(-1)^n \cdot{ }^{3 n-1} C_{n-1}$

2) $(-1)^n \cdot{ }^{3 n-1} C_n$

3) $(-1)^n \cdot{ }^{3 n-1} C_{n+1}$

4) None of these

Solution:

$\mathrm{S}_{\mathrm{n}}={ }^{3 n} \mathrm{C}_0-{ }^{3 n} \mathrm{C}_1+{ }^{3 n} \mathrm{C}_2+\ldots \ldots+(-1)^n \cdot{ }^{3 n} \mathrm{C}_{\mathrm{n}} $

$\text { But }{ }^{3 n} \mathrm{C}_0={ }^{3 n-1} \mathrm{C}_0 $

$-{ }^{3 n} \mathrm{C}_1=--{ }^{3 n-1} \mathrm{C}_0-{ }^{3 n-1} \mathrm{C}_1 $

${ }^{3 n} \mathrm{C}_2={ }^{3 n-1} \mathrm{C}_1+{ }^{3 n-1} \mathrm{C}_2 $

$-{ }^{3 n} \mathrm{C}_3=--{ }^{3 n-1} C_2-{ }^{3 n-1} \mathrm{C}_3 $

$(-1)^n \cdot{ }^{3 n} C_n=(-1)^n \cdot{ }^{3 n-1} C_{n-1}+(-1)^n \cdot{ }^{3 n-1} C_n $

On adding we get

$ S_n=(-1)^n \cdot{ }^{3 n-1} C_n $

Hence, the answer is option (2).

Example 4: The value of $ { }^{50} C_4+\sum_{r=1}^6{ }^{56-r} C_3 \text { is } $

1) ${ }^{55} \mathrm{C}_3$

2) ${ }^{55} C_4$

3) ${ }^{56} C_4$

4) ${ }^{56} C_3$

Solution:

$ { }^{50} C_4+\left({ }^{50} C_3+{ }^{51} C_3+{ }^{52} C_3+\ldots \ldots+{ }^{55} C_3\right) $

Taking the first two terms together and adding them and following the same pattern, we get ${ }^{56} C_4$.

$\left[\mathrm{As}^n C_r+{ }^n C_{r-1}={ }^{n+1} C_r\right] $

Hence, the answer is option (3).

Example 5: The value of the expression ${ }^{(n+1)} C_2+2\left[{ }^2 C_2+{ }^3 C_2+{ }^4 C_2+\ldots . .+{ }^n C_2\right]$ is:

1) $\sum n^3$

2) $\sum n^2$

3) $\sum n$

4) $\frac{n+1}{2}$

Solution:

expression

$ ={ }^{(n+1)} C_2+2\left[{ }^2 C_2+{ }^3 C_2+{ }^4 C_2+\ldots \ldots .\right] $

$={ }^{(n+1)} C_2+2\left[{ }^4 C_3+{ }^4 C_2+\ldots \ldots . .\right] $

$={ }^{(n+1)} C_2+2\left[{ }^5 C_3+{ }^5 C_2+\ldots \ldots .+{ }^n C_2\right] $

$={ }^{(n+1)} C_2+2{ }^{(n+1)} C_3 \text { ultimately } $

$={ }^{(n+1)} C_2+{ }^{(n+1)} C_3+{ }^{(n+1)} C_3 $

$={ }^{(n+2)} C_3+{ }^{(n+1)} C_3=\frac{(n+2)(n+1) n}{6}+\frac{(n+1) n(n-1)}{6} $

$ =\frac{(n)(n+1)(2 n+1)}{6}=\sum n^2 $

Hence, the answer is option (2).

Summary

Binomial theorem is used for the expansion of a binomial expression with a higher degree. Binomial coefficients are the coefficients of the terms in the Binomial expansion. Understanding how to evaluate binomial inside binomial gives an idea to solve more complex problems.