Results on Binomial Theorem

An expression with two terms is called the binomial expansion. In the case of higher degree expression, it is difficult to calculate it. In these cases, Binomial theorem can be used to calculate it manually. Binomial theorem is used for the expansion of a binomial expression with a higher degree. Binomial theorem is proved using the concept of mathematical induction. Apart from Mathematics, Binomial theorem is also used in statistical and financial data analysis.

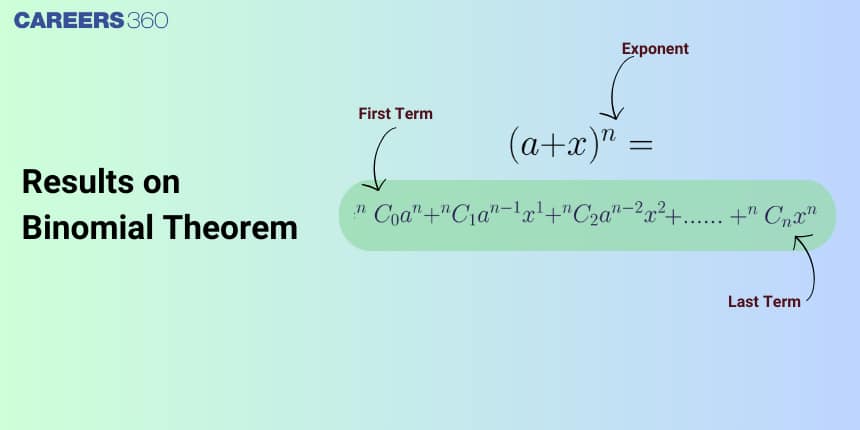
This article is about some results on binomial theorem which falls under the broader category of Binomial Theorem and its applications. It is one of the important topics for competitive exams.

Binomial Theorem

Statement: If $n$ is any positive integer, then

$ (a + b)^n = \binom{n}{0} a^n + \binom{n}{1} a^{n - 1} b + \binom{n}{2} a^{n - 2} b^2 + \dots + \binom{n}{n - 1} a b^{n - 1} + \binom{n}{n} b^n $

Proof:

The proof is obtained by applying the principle of mathematical induction.

Let the given statement be:

$ P(n): (a + b)^n = \binom{n}{0} a^n + \binom{n}{1} a^{n-1} b + \binom{n}{2} a^{n-2} b^2 + \dots + \binom{n}{n-1} a b^{n-1} + \binom{n}{n} b^n $

For $ n = 1 $, we have:

$ P(1): (a + b)^1 = \binom{1}{0} a^1 + \binom{1}{1} b^1 = a + b $

Thus, $ P(1) $ is true.

Suppose $ P(k) $ is true for some positive integer $ k $, i.e.,

$ (a + b)^k = \binom{k}{0} a^k + \binom{k}{1} a^{k-1} b + \binom{k}{2} a^{k-2} b^2 + \dots + \binom{k}{k} b^k$

We shall prove that $ P(k + 1) $ is also true, i.e.,

$ (a + b)^{k + 1} = \binom{k+1}{0} a^{k+1} + \binom{k+1}{1} a^k b + \binom{k+1}{2} a^{k-1} b^2 + \dots + \binom{k+1}{k+1} b^{k+1} $

Now,

$ (a + b)^{k + 1} = (a + b)(a + b)^k $

$ = (a + b) \left[\binom{k}{0} a^k + \binom{k}{1} a^{k-1} b + \binom{k}{2} a^{k-2} b^2 + \dots + \binom{k}{k-1} a b^{k-1} + \binom{k}{k} b^k\right] $

[from (1)]

$ = \binom{k}{0} a^{k+1} + \binom{k}{1} a^k b + \binom{k}{2} a^{k-1} b^2 + \dots + \binom{k}{k-1} a^2 b^{k-1} + \binom{k}{k} a b^k $

$ + \binom{k}{0} a^k b + \binom{k}{1} a^{k-1} b^2 + \binom{k}{2} a^{k-2} b^3 + \dots + \binom{k}{k-1} a b^k + \binom{k}{k} b^{k+1} $

[by actual multiplication]

$ = \binom{k}{0} a^{k+1} + (\binom{k}{1} + \binom{k}{0}) a^k b + (\binom{k}{2} + \binom{k}{1}) a^{k-1} b^2 + \dots + (\binom{k}{k} + \binom{k}{k-1}) a b^k + \binom{k}{k} b^{k+1} $

[grouping like terms]

$ = \binom{k+1}{0} a^{k+1} + \binom{k+1}{1} a^k b + \binom{k+1}{2} a^{k-1} b^2 + \dots + \binom{k+1}{k} a b^k + \binom{k+1}{k+1} b^{k+1}$

(by using $ \binom{k+1}{0} = 1 $, $ \binom{k}{r} + \binom{k}{r-1} = \binom{k+1}{r} $, and $ \binom{k}{k} = 1 = \binom{k+1}{k+1} $)

Thus, it has been proved that $ P(k + 1) $ is true whenever $ P(k) $ is true. Therefore, by the principle of mathematical induction, $ P(n) $ is true for every positive integer $ n $.

Binomial Coefficient

The combination $\binom{n}{r}$ or ${ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}$ occuring in the Binomial theorem is called a Binomial coefficient, where $\binom{n}{r}=C(n, r)={ }^n C_r=\frac{n!}{r!(n-r)!}$.

Theorems on Binomial Theorems

Theorem 1: $2 \leq\left(1+\frac{1}{n}\right)^n<3, \quad n \in \mathbb{N}$

Proof:

Expand, $\left(1+\frac{1}{n}\right)^n$ using binomial theorem

$\left(1+\frac{1}{n}\right)^n =1+n \frac{1}{n}+\frac{n(n-1)}{2!} \frac{1}{n^2}+\frac{n(n-1)(n-2)}{3!} \frac{1}{n^3}+\cdots+\frac{n(n-1)(n-2) \cdots[n-(n-1)]}{n!} \frac{1}{n^n} $

$=1+1+\frac{1}{2!}\left(1-\frac{1}{n}\right)+\frac{1}{3!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)+\cdots+\frac{1}{n!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \cdots\left(1-\frac{n-1}{n}\right) $

$<1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{n!} $

$<1+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^{n-1}}=1+1 \frac{\left\{1-\left(\frac{1}{2}\right)^n\right\}}{1-\frac{1}{2}}=1+2\left\{1-\left(\frac{1}{2}\right)^n\right\}=3-\frac{1}{2^{n-1}} $

Hence, from above

$2 \leq\left(3-\frac{1}{2^{n-1}}\right)<3, n \geq 1 $

$2 \leq \left(1+\frac{1}{n}\right)^n<3, n \geq 1 $

Theorem 2: $\left(\frac{n}{3}\right)^n<n!<\left(\frac{n}{2}\right)^n, n>6$

Recommended Video Based on Results on Binomial Theorem:

Solved Examples Based on Results on Binomial Theorem

Example 1: If $y=(x)^{3 x}$ for $\mathrm{x}>2$, which of the following is true?

1) $y<(3 x)$ !

2) $y<x!$

3) $(3 x)!<(1.5 x)^{3 x}$

4) Both 1 and 3

Solution:

As we know, $\left(\frac{n}{3}\right)^n<n!<\left(\frac{n}{2}\right)^n$, this result valid for $n>6$

Let $n=3 x$

Hence, $x=\frac{n}{3}$ hence, $n>6$

Now, ${ }^y=\left(\frac{n}{3}\right)^n$

Hence,

$\left(\frac{n}{3}\right)^n<n!<\left(\frac{n}{2}\right)^n $

$ \text { or, } $

$ (x)^{3 x}<(3 x)!<(1.5 x)^{3 x} $

Hence, the answer is option 4.

Example 2: What is the value of an integer just less than $y=\left(\frac{101}{100}\right)^{100}$ ?

1) $0$

2) $1 $

3) $2 $

4) $3 $

Solution:

$2 \leq\left(1+\frac{1}{n}\right)^n<3, \quad n \in \mathbb{N} $

Now,

$y=\left(\frac{101}{100}\right)^{100} $

It can be written as $y=\left(1+\frac{1}{100}\right)^{100}$

hence, $2 \leq y<3$

Hence, the answer is option 3.

Example 3: Suppose $\sum_{r=0}^{2023} r^{22023} C_r=2023 \times \alpha \times 2^{2022}$ Then the value of $\alpha$ is

1) $1012 $

2) $2010 $

3) $1320 $

4) $1200 $

Solution:

$\sum_{r=0}^n \mathrm{r}^{2 n} C_r $

$ =\sum_{r=0}^n r^2 \cdot \frac{n}{r}{ }^{n-1} C_{r-1} $

$ =n \sum_{r=1}^n\left((r-1)^{n-1} C_{r-1}+{ }^{n-1} C_{r-1}\right) $

$ =n \sum_{r=2}^n(n-1)^{n-2} C_{r-2}+n \sum_{r=1}^n{ }^{n-1} C_{r-1} $

$=n(n-1)\left[2^{n-2}\right]+n\left[2^{n-1}\right] $

$=2023 \cdot 2022 \cdot 2^{2021}+2023 \cdot 2^{2022} $

$=2023 \cdot 2^{2021}[2022+2] $

$=2023 \cdot 2^{2021} \cdot 2024 $

$=2023 \cdot 1012 \cdot 2^{2022} \Rightarrow \alpha=1012 $

Hence, the answer is $1012$.

Example 4: The value of the natural numbers $\underline{n}$ such that the inequality $2^n>2 n+1$ is valid:

1) For $n \geq 3$

2) For $n<3$

3) For $m$

4) For any $n$

Solution:

Check through the options, the condition $2^n>2 n+1$ is valid for $n \geq 3$.

Hence, the answer is option (1).

Example 5: The greater of the two numbers $100^{300}$ and $300!$ is ....

1) $300!$

2) $200!$

3) Both of the above

4) None of the above

Solution:

For $n>6$,

$ \left(\frac{n}{3}\right)^n<n!<\left(\frac{n}{2}\right)^n$

$ \Rightarrow \quad\left(\frac{n}{3}\right)^n<n! $

Putting $n=300$

$\therefore(100)^{300}<300! $

$\text { i.e. } 300! $

Hence, the answer is option (1).