Projection Formula & Overview

Projection Formula

In a geometric sense, projecting a vector onto another vector means finding the shadow or footprint of one vector along the direction of another.

Given two vectors $\mathbf{a}$ and $\mathbf{b}$, the projection of $\mathbf{a}$ onto $\mathbf{b}$ is a vector that lies along $\mathbf{b}$ and represents the component of $\mathbf{a}$ in the direction of $\mathbf{b}$.

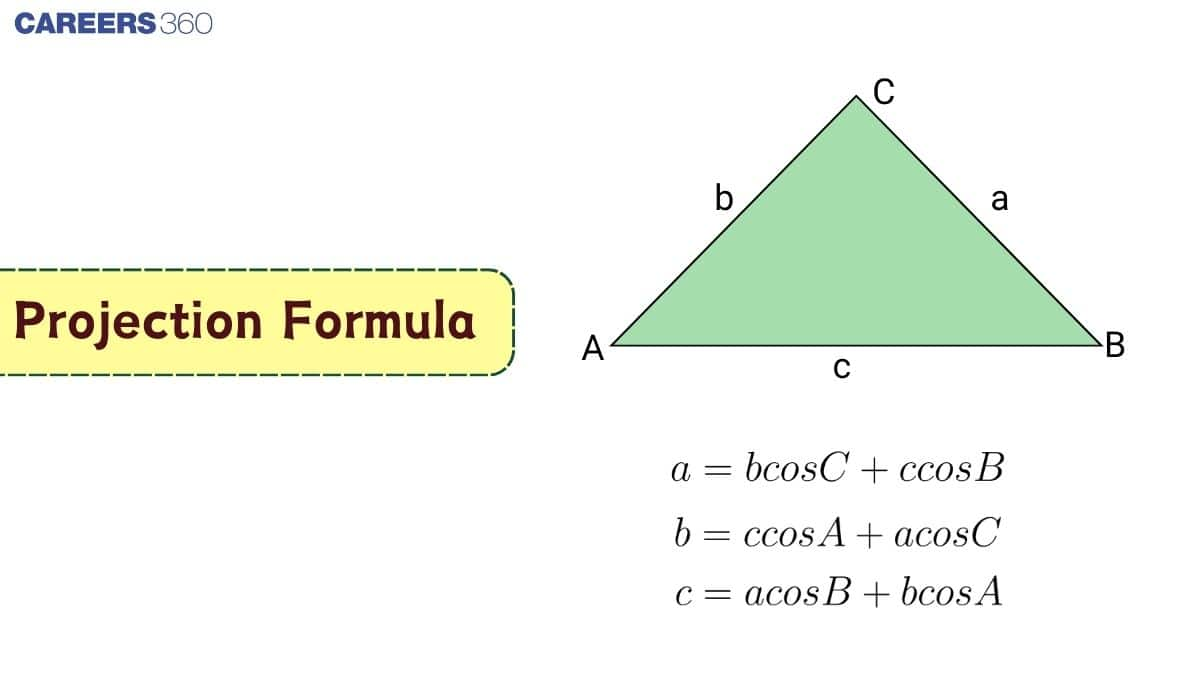
In the $\triangle ABC$, Projection of $AB$ on $BC$ is $BD$ and Projection of $AC$ on $BC$ is $DC$.

Now,

$BD = c \cos B \quad \text{and} \quad DC = b \cos C$

and, $BC = a = BD + DC$

$= c \cos B + b \cos C$

$a = c \cos B + b \cos C$

In a similar way, other projection formulas can be derived:

1. $a = c \cos B + b \cos C$

2. $b = c \cos A + a \cos C$

3. $c = b \cos A + a \cos B$

In any triangle ABC we have,

$a \sin A = b \sin B = c \sin C = 2R \quad --------- \ldots (1)$

Now convert the above relation into sides in terms of angles in terms of the sides of any triangle.

$\dfrac{a}{\sin A} = 2R$

$\Rightarrow a = 2R \sin A \quad --------- \ldots (2)$

$\dfrac{b}{\sin B} = 2R$

$\Rightarrow b = 2R \sin B \quad ---------- \ldots (3)$

$\dfrac{c}{\sin C} = 2R$

$\Rightarrow c = 2R \sin C \quad ----------- \ldots (4)$

Case 1.

(i) $a = b \cos C + c \cos B$

Now,
$b \cos C + c \cos B$

$= 2R \sin B \cos C + 2R \sin C \cos B$

$= 2R \sin (B + C)$

$= 2R \sin (\pi - A)$, [Since $A + B + C = \pi$]

$= 2R \sin A$

$= a$ [From (2)]

Therefore, $a = b \cos C + c \cos B$

Case 2.

(ii) b = c cos A + a cos C

Now, $c \cos A + a \cos C$

$= 2R \sin C \cos A + 2R \sin A \cos C$

$= 2R \sin (A + C)$

$= 2R \sin (\pi - B)$, [Since $A + B + C = \pi$]

$= 2R \sin B$

$= b$ [From (3)]

Therefore, $b = c \cos A + a \cos C$

Case 3.

(iii) c = a cos B + b cos A

Now, $a \cos B + b \cos A$

$= 2R \sin A \cos B + 2R \sin B \cos A$

$= 2R \sin (A + B)$

$= 2R \sin (\pi - C)$, [Since $A + B + C = \pi$]

$= 2R \sin C$

$= c$ [From (4)]

Therefore, $c = a \cos B + b \cos A$

Projection Formula Derivation

The projection formula derivation can be understood in two main ways: one using trigonometry and the other using the dot product projection formula. Both approaches show how one side or vector can be expressed as the projection of another.

Using Trigonometry for Derivation

In any triangle $ABC$, if we project side $b$ and $c$ onto side $a$, we get:
$a = b \cos C + c \cos B$
This comes from dropping perpendiculars and applying basic trigonometric ratios. Similarly, we can derive:
$b = c \cos A + a \cos C$
$c = a \cos B + b \cos A$
These three relations are collectively known as the projection formulas in trigonometry. They are often used in Class 11 maths for problem solving.

Using Dot Product Projection Formula for Derivation

For two vectors $\mathbf{a}$ and $\mathbf{b}$, the dot product projection formula is:
$\text{Projection of } \mathbf{a} \text{ on } \mathbf{b} = \dfrac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|}$
If we want the projection in vector form, it is written as:
$\dfrac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^2} , \mathbf{b}$
This shows the component of one vector along another vector and is the vector version of the scalar projection formula.

Scalar Projection Formula

The scalar projection formula gives the length of the projection of one vector onto another. It is also called the component of a vector in a given direction.

Scalar Projection Formula Derivation

If $|\mathbf{a}|$ is the length of vector $\mathbf{a}$ and $\theta$ is the angle between $\mathbf{a}$ and $\mathbf{b}$, then the scalar projection is:
$\text{Scalar Projection} = |\mathbf{a}| \cos \theta$
This is derived directly using right triangles and basic trigonometric ratios.

Examples of Scalar Projection Formula

1. If $|\mathbf{a}| = 10$ units and $\theta = 60^\circ$, then the projection is:
   $10 \cos 60^\circ = 5$ units.

2. If $|\mathbf{a}| = 8$ units and $\theta = 30^\circ$, then the projection is:
   $8 \cos 30^\circ = 4\sqrt{3}$ units.

Vector Projection Formula

The vector projection formula not only gives the length but also the direction of the projection. It tells us how much of vector $\mathbf{a}$ lies along vector $\mathbf{b}$.

Formula of Projection of Vector Using Dot Product

The vector projection of $\mathbf{a}$ on $\mathbf{b}$ is:
$\text{Proj}_{\mathbf{b}} \mathbf{a} = \dfrac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^2} , \mathbf{b}$
This formula is derived using the dot product and is very useful in physics, geometry, and engineering applications.

Vector Projection Formula in Trigonometry

In trigonometry, the projection of one side of a triangle on another is expressed using cosine:
$a = b \cos C + c \cos B$
This connects the geometric idea of projection with trigonometric ratios, making it easier to solve projection formula problems and solutions in Class 11 maths.

Step-by-Step Derivation of Vector Projection Formula

1. Take two vectors $\mathbf{a}$ and $\mathbf{b}$ with angle $\theta$ between them.

2. The length of projection is given by the scalar projection formula: $|\mathbf{a}| \cos \theta$.

3. To convert this into a vector form along $\mathbf{b}$, we multiply by the unit vector of $\mathbf{b}$:
   $\dfrac{\mathbf{b}}{|\mathbf{b}|}$

4. Therefore, the final vector projection formula is:
   $\text{Proj}_{\mathbf{b}} \mathbf{a} = \dfrac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^2} , \mathbf{b}$

Common Mistakes in Solving Projection Questions

While solving projection formula problems and solutions, students often make small errors that lead to wrong answers.

1. Confusing scalar projection formula ($a \cos \theta$) with vector projection formula.

2. Forgetting that $\cos (\pi - \theta) = -\cos \theta$, which changes the sign of the projection.

3. Using wrong angle in the triangle (taking $\sin$ instead of $\cos$).

4. Mixing up which side is being projected onto which.

5. Not applying the sine rule ($\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$) before substitution.

Short Tricks to Remember Projection Formula

To quickly recall the projection of a vector on another vector in trigonometry, keep these points in mind:

1. The formula always involves law of cosines i.e. cosine of the angle between the side and the line of projection.

2. Remember the three standard relations:

   • $a = b \cos C + c \cos B$

   • $b = c \cos A + a \cos C$

   • $c = a \cos B + b \cos A$

3. Think of projection as the shadow of one side on another side.

4. Use the mnemonic: “Side = sum of other two sides × cosine of opposite angles.”

Solved Examples Based on the Projection Formula

Example 1: In Triangle ABC , point D is on BC is such that $A D \perp B C$ and E is the middle point of BC and $b^2+2 a^2=c^2$ distance between D and E is?
1) b
2) $\frac{a+b+c}{2}$
3) $\frac{b+c}{2}$
4) a

Solution:

$\begin{aligned}
D E & =E C-D C \\
& =\frac{a}{2}-b \cos C \\
& =\frac{a}{2}-b \frac{a^2+b^2-c^2}{2 a b} \\
& =\frac{a}{2}-b \frac{a^2-\left(c^2-b^2\right)}{2 a b} \\
& =\frac{a}{2}-\frac{a^2-\left(2 a^2\right)}{2 a} \\
& =a
\end{aligned}$

Example 2: In triangle $A B C$ if $a+c-\frac{3 b}{2}=a \sin ^2\left(\frac{C}{2}\right)+c \sin ^2\left(\frac{A}{2}\right)$ then a,b,c are in ?

1) A.P.

2) G.P.

3) H.P.

4) None of these

Solution:

$\begin{aligned}
& \quad a+c-\frac{3 b}{2}=a \sin ^2\left(\frac{C}{2}\right)+c \sin ^2\left(\frac{A}{2}\right) \\
& a+c-\frac{3 b}{2}=a\left[\frac{1-\cos C}{2}\right]+c\left[\frac{1-\cos A}{2}\right] \\
& c \cos A+a \cos C=3 b-a-c \\
& b=3 b-a-c
\end{aligned}$

by above triangle $c \cos A+a \cos C=b$
a+c=2 b
$$

$a, b, c$ in $A . P$.
Example 3: The value of $b \cos C+c \cos B$ is:
1) $-a$
2) a
3) b
4) c

Solution:
Given that,

$
b \cos C+c \cos B
$

Using the law of cosine,

$\begin{aligned}
& b \cos C+c \cos B=b\left[\frac{\left(a^2+b^2-c^2\right)}{2 a b}\right]+c\left[\frac{\left(c^2+a^2-b^2\right)}{2 c a}\right] \\
& b \cos C+c \cos B=\left[\frac{\left(a^2+b^2-c^2+c^2+a^2+b^2\right)}{2 a}\right]
\end{aligned}$

$
b \cos C+c \cos B=\frac{2 a^2}{2 a}
$

$b \cos C+c \cos B=a$
Hence, the answer is the option (2).

Example 4: If the sides of the $\triangle A B C$ are $a=3, b=2$ and $c=4$, then the value of $3 \cos B+2 \cos C$ is:
1) $\frac{4}{5}$
2) $-\frac{4}{5}$
3) $\frac{2}{5}$
4) $-\frac{2}{5}$

Solution:
Given that,
$\begin{aligned}
& 3 \cos B+2 \cos C \\
& \cos B=\frac{a^2+c^2-b^2}{2 a c} \\
& \cos B=\frac{9+16-4}{24} \\
& \cos B=\frac{21}{24}
\end{aligned}$

$\begin{aligned}
& \cos C=\frac{a^2+b^2-c^2}{2 a b} \\
& \cos C=\frac{-1}{4}
\end{aligned}$
Therefore,

$\begin{aligned}
& 3 \cos B+2 \cos C=2 \times \frac{21}{24}+2 \times \frac{-1}{4} \\
& 3 \cos B+2 \cos C=\frac{21}{12}-\frac{1}{2} \\
& 3 \cos B+2 \cos C=\frac{4}{5}
\end{aligned}$
Hence, the answer is option (1).

Example 5: If the area of the $\triangle A B C$ be $\Delta$, then the value of $b^2 \sin 2 C+c^2 \sin 2 B$ is:
1) $3 \Delta$
2) $2 \Delta$
3) $4 \Delta$
4) $5 \Delta$

Solution:
Given that,

$
\begin{aligned}
& b^2 \sin 2 C+c^2 \sin 2 B \\
& b^2 \sin 2 C+c^2 \sin 2 B=b^2 2 \sin C \cos C+c^2 2 \sin B \cos B \\
& b^2 \sin 2 C+c^2 \sin 2 B=2 b \cos C \cdot b \sin C+2 c \cos B \cdot c \sin B
\end{aligned}
$

We know that,

$
\frac{a}{\sin B}=\frac{c}{\sin C} \Rightarrow b \sin C=c \sin B
$

Thus,

$
\begin{aligned}
& b^2 \sin 2 C+c^2 \sin 2 B=2 b \cos C \cdot c \sin B+2 c \cos B \cdot c \sin B \\
& b^2 \sin 2 C+c^2 \sin 2 B=2 c \sin B(b \cos C+c \cos B)
\end{aligned}
$

We know that,

$
a=b \cos C+c \cos B
$
Therefore,

$b^2 \sin 2 C+c^2 \sin 2 B=2 c \sin B \cdot a^{b^2 \sin 2 C+c^2 \sin 2 B=4 \cdot \frac{1}{2} a c \sin B} b^2 \sin 2 C+c^2 \sin 2 B=4 \Delta$

Hence, the answer is option (3).

List of Topics Related to the Projection Formula

Explore the list of topics related to the projection formula to get a clear overview of its applications in trigonometry. These topics make problem-solving easier in exams.

NCERT Resources

NCERT resources are the most reliable for building a clear understanding of trigonometric functions. They explain concepts simply, offer solved examples, and give enough practice for exams. Below are the key NCERT study materials for Class 11 Chapter 3 – Trigonometric Functions.

NCERT Class 11 Maths Notes for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Solutions for Chapter 3 - Trigonometric Functions

NCERT Class 11 Maths Exemplar Solutions for Chapter 3 - Trigonometric Functions

Practice Questions based on Projection Formula

Solve these practice questions based on the projection formula to strengthen your understanding of trigonometry. These problems will help you apply the formula in different cases and improve accuracy for exams.

Projection Formula - Practice Question MCQ

You can practice the related questions from the links shared below: