Trigonometric Identities

What are Trigonometric Identities?

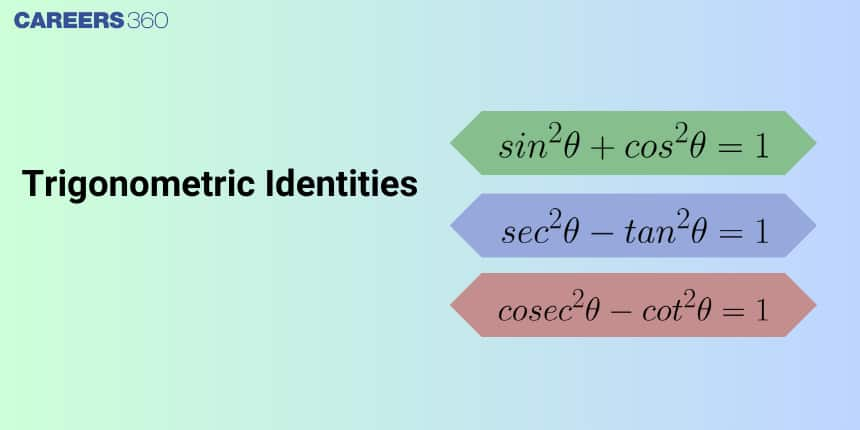
Trigonometric Identities are the relationship which involve different trigonometric ratios which hold true for all the value of angles within the equation. These identities represent the relationship between the angles of a right angle triangle, and its sides. Here the ratios are defined on the basis of sides of a right angled triangle, such as the adjacent side, opposite side and the longest side(being hypotenuse). There are six trigonometric ratios namely as the sine, cosine, tangent, cotangent, secant and cosecant.

List of Trigonometric Identities

In trigonometry, trigonometric identities are equations involving trigonometric ratios that are true for all values of an angle (where the expressions are defined). These identities are extremely useful for simplifying expressions, solving trigonometric equations, proving results, and applying concepts in geometry, calculus, physics, and engineering.

Trigonometric identities are usually grouped based on their origin and application, as explained below.

Pythagorean Trigonometric Identities

Pythagorean identities are derived from the Pythagoras theorem applied to a right-angled triangle. They show fundamental relationships between sine, cosine, tangent, and their reciprocal ratios.

The most important Pythagorean identity states that the sum of the squares of sine and cosine of an angle is always equal to one:

$\sin^2 t + \cos^2 t = 1$

Using this identity, we also obtain relationships involving tangent, secant, cotangent, and cosecant:

$1 + \tan^2 t = \sec^2 t$

$1 + \cot^2 t = \csc^2 t$

These identities are frequently used to simplify trigonometric expressions and prove other identities.

Reciprocal Trigonometric Identities

Reciprocal identities define the relationship between a trigonometric ratio and its reciprocal. They allow us to express sine, cosine, and tangent in terms of cosecant, secant, and cotangent.

The reciprocal identities are:

$\csc t = \dfrac{1}{\sin t}$

$\sec t = \dfrac{1}{\cos t}$

$\cot t = \dfrac{1}{\tan t}$

These identities are especially helpful when converting one trigonometric ratio into another during problem solving.

Addition of Angles Trigonometric Identities (Sum Formulae)

Addition identities are used to find the trigonometric values of the sum of two angles. These formulas are useful in simplifying expressions and solving equations involving multiple angles.

If $A$ and $B$ are two angles, then:

$\sin(A + B) = \sin A \cos B + \cos A \sin B$

$\cos(A + B) = \cos A \cos B - \sin A \sin B$

$\tan(A + B) = \dfrac{\tan A + \tan B}{1 - \tan A \tan B}$

Difference of Angles Trigonometric Identities (Subtraction Formulae)

Difference identities help evaluate trigonometric expressions involving the difference of two angles.

If $A$ and $B$ are two angles, then:

$\sin(A - B) = \sin A \cos B - \cos A \sin B$

$\cos(A - B) = \cos A \cos B + \sin A \sin B$

$\tan(A - B) = \dfrac{\tan A - \tan B}{1 + \tan A \tan B}$

These identities are widely used in problem-solving and identity verification.

Double-Angle Trigonometric Identities

Double-angle identities express trigonometric ratios of $2A$ in terms of a single angle $A$. They are derived using addition identities by substituting $A = B$.

The commonly used double-angle identities are:

$\sin(2A) = 2 \sin A \cos A$

$\cos(2A) = \cos^2 A - \sin^2 A$

$\cos(2A) = 2 \cos^2 A - 1$

$\cos(2A) = 1 - 2 \sin^2 A$

$\tan(2A) = \dfrac{2 \tan A}{1 - \tan^2 A}$

These identities are useful for simplifying expressions and solving trigonometric equations.

Trigonometric Identities of Allied Angles

Two angles are called allied angles if their sum or difference is a multiple of $90^\circ$ or $\dfrac{\pi}{2}$. These identities help evaluate trigonometric ratios of non-standard angles.

Allied Angles of the Form $90^\circ - \theta$

$\sin(90^\circ - \theta) = \cos \theta$

$\cos(90^\circ - \theta) = \sin \theta$

$\tan(90^\circ - \theta) = \cot \theta$

Allied Angles of the Form $180^\circ - \theta$

$\sin(180^\circ - \theta) = \sin \theta$

$\cos(180^\circ - \theta) = -\cos \theta$

$\tan(180^\circ - \theta) = -\tan \theta$

Allied Angles of the Form $180^\circ + \theta$

$\sin(180^\circ + \theta) = -\sin \theta$

$\cos(180^\circ + \theta) = -\cos \theta$

$\tan(180^\circ + \theta) = \tan \theta$

Triple-Angle Trigonometric Identities

Triple-angle identities express trigonometric functions of $3A$ in terms of $A$. These are useful in advanced trigonometric simplifications.

$\sin(3A) = 3 \sin A - 4 \sin^3 A$

$\cos(3A) = 4 \cos^3 A - 3 \cos A$

$\tan(3A) = \dfrac{3 \tan A - \tan^3 A}{1 - 3 \tan^2 A}$

Trigonometric Identities of Opposite Angles

Opposite angle identities describe how trigonometric ratios behave when the angle is negative.

$\sin(-A) = -\sin A$

$\cos(-A) = \cos A$

$\tan(-A) = -\tan A$

These identities are important in coordinate geometry and graph-based problems.

Ratio Trigonometric Identities

Ratio identities express one trigonometric ratio in terms of others and are often used for simplification.

$\tan \theta = \dfrac{\sin \theta}{\cos \theta}$

$\cot \theta = \dfrac{\cos \theta}{\sin \theta}$

Triangle Identities (Applicable to All Triangles)

Unlike earlier identities, triangle identities apply to all triangles, not just right-angled ones.

Sine Rule

The ratio of the sine of an angle to its opposite side is the same for all three angles of a triangle:

$\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}$

Cosine Rule

The cosine rule relates the sides and angles of a triangle and is a generalization of the Pythagoras theorem:

$\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}$

Tangent Rule

The tangent rule relates the difference and sum of two sides to the difference of the opposite angles:

$\tan\left(\dfrac{A - B}{2}\right) = \dfrac{a - b}{a + b} \cot\left(\dfrac{C}{2}\right)$

Applications of Trigonometric Identities

Trigonometric identities are used in many areas of mathematics and science. Some key applications include:

• Simplifying complex trigonometric expressions

• Solving trigonometric equations efficiently

• Proving trigonometric identities in exams

• Finding exact values of trigonometric ratios

• Solving problems on heights and distances

• Applying concepts in geometry and calculus

• Using trigonometry in physics and engineering problems

Solved Examples Based on Trigonometric Identities

Example 1: For a triangle $A B C$, the value of $\cos 2 A+\cos 2 B+\cos 2 C$ is least. If its inradius is 3 and incentre is $M$, then which of the following is NOT correct? [JEE MAINS 2023]
1) The perimeter of $\triangle A B C$ is $18 \sqrt{3}$
2) $\sin 2 A+\sin 2 B+\sin 2 C=\sin A+\sin B+\sin C$
3) $\overrightarrow{M A} \cdot \overrightarrow{M B}=-18$
4) The area of $\triangle A B C$ is $\frac{27 \sqrt{3}}{2}$

Solution:
Let P
$=\cos 2 \mathrm{~A}+\cos 2 \mathrm{~B}+\cos 2 \mathrm{C}$
$=2 \cos (\mathrm{A}+\mathrm{B}) \cos (\mathrm{A}-\mathrm{B})+2 \cos ^2 \mathrm{C}-1$
$=2 \cos (\pi-\mathrm{C}) \cos (\mathrm{A}-\mathrm{B})+2 \cos ^2 \mathrm{C}-1$
$=-2 \cos \mathrm{C}[\cos (\mathrm{A}-\mathrm{B})+\cos (\mathrm{A}+\mathrm{B})]-1$
$=-1-4 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}$
for $P$ to be the minimum
$\cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}$ must be maximum
$\Rightarrow \triangle \mathrm{ABC}$ is an equilateral triangle

Let the side length of the triangle be a

Example 2: Let $f_k(x)=\frac{1}{k}\left(\sin ^k+\cos ^k x\right)$ for $\mathrm{k}=1,2,3, \ldots .$. Then for all real values of x , the value of $f_4(x)-f_6(x)$ is equal to:
1) $\frac{1}{4}$
2) $\frac{-1}{12}$
3) $\frac{5}{12}$
4) $\frac{1}{12}$

Solution:

$f_4(x) = \dfrac{1}{4}\left(\sin^4 x + \cos^4 x\right)$

$= \dfrac{1}{4}\left[\left(\sin^2 x + \cos^2 x\right)^2 - 2\sin^2 x \cos^2 x\right]$

$= \dfrac{1}{4}\left[1 - 2\sin^2 x \cos^2 x\right]$

$= \dfrac{1}{4} - \dfrac{1}{2}\sin^2 x \cos^2 x$

$f_6(x) = \dfrac{1}{6}\left(\sin^6 x + \cos^6 x\right)$

$= \dfrac{1}{6}\left[\left(\sin^2 x + \cos^2 x\right)^3 - 3\sin^4 x \cos^2 x - 3\sin^2 x \cos^4 x\right]$

$= \dfrac{1}{6}\left[1 - 3\sin^2 x \cos^2 x\left(\sin^2 x + \cos^2 x\right)\right]$

$= \dfrac{1}{6} - \dfrac{1}{2}\sin^2 x \cos^2 x$

$f_4(x) - f_6(x) = \dfrac{1}{4} - \dfrac{1}{6}$

$= \dfrac{1}{12}$

Hence, the answer is Option 4.

Example 3: If $15 \sin ^4 \alpha+10 \cos ^4 \alpha=6$ for some $\alpha \epsilon R$, then the value of $27 \sec ^6 \alpha+8 \operatorname{cosec}^6 \alpha$ is equal to: [JEE MAINS 2021]
1) 350
2) 250
3) 400
4) 500

Solution

$15\sin^4 \alpha + 10\cos^4 \alpha = 6$

$15\sin^4 \alpha + 10\cos^4 \alpha = 6\left(\sin^2 \alpha + \cos^2 \alpha\right)^2$

$\left(3\sin^2 \alpha - 2\cos^2 \alpha\right)^2 = 0$

$\tan^2 \alpha = \dfrac{2}{3}$

$\Rightarrow \cot^2 \alpha = \dfrac{3}{2}$

$27\sec^6 \alpha + 8\csc^6 \alpha$

$= 27\left(1 + \tan^2 \alpha\right)^3 + 8\left(1 + \cot^2 \alpha\right)^3$

$= 27\left(1 + \dfrac{2}{3}\right)^3 + 8\left(1 + \dfrac{3}{2}\right)^3$

$= 27\left(\dfrac{5}{3}\right)^3 + 8\left(\dfrac{5}{2}\right)^3$

$= 125 + 125$

$= 250$

Hence, the answer is Option 3.

Example 4: Let $S=\left\{\theta \epsilon[-2 \pi, 2 \pi]: 2 \cos ^2 \theta+3 \sin \theta=0\right\}$. Then the sum of the elements of $S$ is: [JEE MAINS 2019]
1) $\frac{13 \pi}{6}$
2) $\frac{5 \pi}{3}$
3) $2 \pi$
4) $\pi$

Solution:

Given equation

Hence, the answer is option 3.

Example 5: If $\frac{\sqrt{2} \sin \alpha}{\sqrt{1+\cos 2 \alpha}}=\frac{1}{7}$ and $\sqrt{\frac{1-\cos 2 \beta}{2}}=\frac{1}{\sqrt{10}}, \alpha, \beta \space\epsilon\left(0, \frac{\pi}{2}\right)$, then $\tan (\alpha+2 \beta)$ is equal to

1) 0

2) 1

3) 0.5

4) 2

Solution:

$\dfrac{\sqrt{2}\sin \alpha}{\sqrt{2}\cos \alpha} = \dfrac{1}{7}$

$\tan \alpha = \dfrac{1}{7}$

$\sin \beta = \dfrac{1}{\sqrt{10}}$

$\tan \beta = \dfrac{1}{\sqrt{3}}$

$\tan 2\beta = \dfrac{2\tan \beta}{1 - \tan^2 \beta}$

$= \dfrac{2 \cdot \dfrac{1}{\sqrt{3}}}{1 - \dfrac{1}{3}}$

$= \dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{2}{3}}$

$= \dfrac{3}{\sqrt{3}}$

$= \sqrt{3}$

$\tan(\alpha + 2\beta) = \dfrac{\tan \alpha + \tan 2\beta}{1 - \tan \alpha \tan 2\beta}$

$= \dfrac{\dfrac{1}{7} + \sqrt{3}}{1 - \dfrac{\sqrt{3}}{7}}$

$= 1$

Hence, the answer is option 2.

List of Topics Related to the Trigonometric Ratios

This section provides a structured list of topics related to trigonometric ratios, covering both fundamental and advanced concepts required for school-level mathematics and competitive exams. It highlights connected areas such as angle measurement, allied and compound angles, function signs, identities, graphs, and special formulas, helping learners plan a complete and systematic study.

NCERT Resources

This section brings together important NCERT resources for Class 11 Chapter 3 - Trigonometric Functions, curated to build a strong conceptual foundation. It includes concise notes, step-by-step NCERT solutions, and exemplar problems, helping students understand trigonometric ratios and functions effectively and prepare confidently for exams.

NCERT Class 11 Chapter 3 Trigonometric Functions Notes

NCERT Class 11 Chapter 3 Trigonometric Functions Solutions

NCERT Exemplar Class 11 Chapter 3 Trigonometric Functions

Practice Questions based on Trigonometric Identities

This section offers targeted practice questions on trigonometric identities, ranging from basic concepts to advanced applications. It covers key areas like signs of trigonometric functions, graphs, allied and compound angles, sum–product formulas, and multiple-angle identities, helping students strengthen problem-solving skills for school and competitive exams.

Trigonometric Identities - Practice Question

Below is the list of the next topics which you can practice: