Definite Integrals of Piecewise Functions

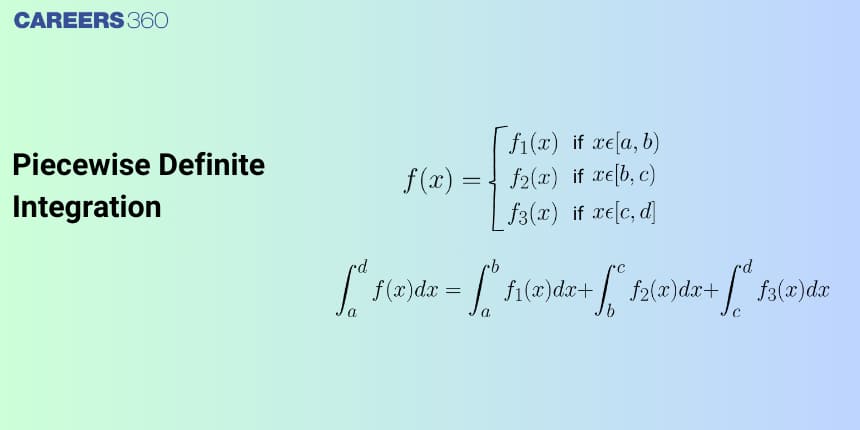
Piecewise Definite Integration

Definite integration deals with finding the exact area under a curve between two fixed limits on the x-axis. If a function is continuous and differentiable, we simply apply the Fundamental Theorem of Calculus and evaluate $F(b)-F(a)$. However, real mathematical functions are not always so smooth—many are piecewise, discontinuous, or change their algebraic form across an interval. In such cases, definite integration must be broken into smaller intervals to handle each “piece” correctly.

Let $f(x)$ be defined on the closed interval $[a,b]$, and let $F(x)$ be its antiderivative such that $\frac{d}{dx}F(x)=f(x)$. Then the definite integral is
$\int_a^b f(x),dx = F(b) - F(a)$.

Below are the essential properties of definite integrals, followed by the detailed property that applies to piecewise functions.

Important Properties of Definite Integrals

Understanding the core properties of definite integrals makes solving complex problems so much easier, almost like having a built-in shortcut system. This section walks you through the most essential properties that simplify evaluation, break down tricky intervals, and help you solve integrals faster and more accurately.

Property 1: Zero Interval Rule

If both limits are equal, no area exists.
$\int_a^a f(x),dx = 0$

Property 2: Independence of Dummy Variable

Changing the variable does not affect the value of the integral.
$\int_a^b f(x),dx = \int_a^b f(t),dt = \int_a^b f(y),dy$

Property 3: Reversal of Limits

Swapping the limits changes the sign.
$\int_a^b f(x),dx = -\int_b^a f(x),dx$

Property 4: King’s Property

A powerful symmetry property used frequently in competitive exams.
$\int_a^b f(x),dx = \int_a^b f(a+b-x),dx$

Property 5: Piecewise Definite Integration

If $c$ lies between $a$ and $b$, then
$\int_a^b f(x),dx = \int_a^c f(x),dx + \int_c^b f(x),dx$

This is extremely useful when:

• the function changes its formula at $x=c$
• the function is discontinuous at $c$
• the function becomes non-differentiable at $c$
• different sub-intervals give simpler integrals

Proof

If $\frac{d}{dx}F(x)=f(x)$, then
$\int_a^c f(x),dx + \int_c^b f(x),dx
= [F(x)]_a^c + [F(x)]_c^b
= F(c)-F(a) + F(b)-F(c)
= F(b)-F(a)
= \int_a^b f(x),dx$

This verifies the correctness of splitting definite integrals across breakpoints.

Generalized Version

If multiple breakpoints exist,
$\int_a^b f(x),dx = \int_a^{c_1} f(x),dx + \int_{c_1}^{c_2} f(x),dx + \cdots + \int_{c_n}^b f(x),dx$

Property 6: Symmetric Splitting from 0 to a

$\int_0^a f(x),dx = \int_0^{a/2} f(x),dx + \int_0^{a/2} f(a-x),dx$

Proof

From Property 5,
$\int_0^a f(x),dx = \int_0^{a/2}f(x),dx + \int_{a/2}^a f(x),dx$

Let $x=a-t \Rightarrow dx=-dt$.
When $x=\frac{a}{2}$, $t=\frac{a}{2}$; when $x=a$, $t=0$.

Thus,
$\int_{a/2}^a f(x),dx
= \int_{a/2}^0 f(a-t)(-dt)
= \int_0^{a/2} f(a-t),dt$

Hence,
$\int_0^a f(x),dx = \int_0^{a/2} f(x),dx + \int_0^{a/2} f(a-x),dx$

This identity is widely used in symmetrical integrals and in problems involving even–odd functions.

Handling Absolute Value Functions in Definite Integrals

Many piecewise functions arise from expressions like $|x|$, $|x-2|$, or $|x+1|$.
To integrate such functions:

1. Identify where the expression inside the absolute value becomes zero.

2. Break the integral at those points.

3. Replace $|g(x)|$ with $\pm g(x)$ depending on sign in each interval.

Example:
$\int_{-3}^{4} |x-1|,dx$
Split at $x=1$, then evaluate on $[-3,1]$ and $[1,4]$ separately.

Definite Integrals of Step Functions and Floor/Ceil Functions

Functions like $[x]$ (greatest integer) or ${x}$ (fractional part) are classic examples of piecewise definitions.

Key ideas:

• Each integer creates a new interval.
• Evaluate integrals separately on each interval:
$\int_0^5 [x],dx = \int_0^1 0,dx + \int_1^2 1,dx + \cdots + \int_4^5 4,dx$

This concept is heavily used in JEE and other entrance exams.

Piecewise Integration in Trigonometric Domains

Trigonometric functions may also change their behaviour over intervals:

• $\sin x$ changes sign at multiples of $\pi$
• $\cos x$ changes sign at odd multiples of $\frac{\pi}{2}$
• $\tan x$ has discontinuities at odd multiples of $\frac{\pi}{2}$

Whenever the integrand involves absolute values, sign changes, or discontinuity points, splitting the interval becomes mandatory.

Applications of Piecewise Definite Integration

• Calculating total cost when unit price changes beyond a threshold
• Computing distance when velocity function changes across time intervals
• Probability density functions defined piecewise
• Area under curves with non-smooth edges
• Modelling real-world systems with discontinuities (e.g., electric circuits, signals)

Solved Examples Based on Piecewise Definite Integration:

Example 1: The integral $\int_0^\pi \sqrt{1+4 \sin ^2 \frac{x}{2}-4 \sin \frac{x}{2}} d x$ equals:

1) $4 \sqrt{3}-4$
2) $4 \sqrt{3}-4-\frac{\pi}{3}$
3) $\pi-4$
4) $\frac{2 \pi}{3}-4-4 \sqrt{3}$

Solution

As learnt in concept

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$\begin{aligned} & =\int_0^\pi \sqrt{\left(1-2 \sin \frac{x}{2}\right)^2}=\int_0^\pi\left|1-2 \sin \frac{x}{2}\right| d x \\ & \int_0^{\frac{\pi}{3}} \sqrt{\left(1-2 \sin \frac{x}{2}\right)}=\int_{\frac{\pi}{4}}^\pi\left(1-2 \sin \frac{x}{2}\right) d x \\ & \left(x+4 \cos \frac{x}{2}\right)_0^{\frac{\pi}{3}}-\left(x+4 \cos \frac{x}{2}\right)^\pi \\ & =4 \sqrt{3}-4-\frac{\pi}{3}\end{aligned}$

Example 2: The value of $\int_1^a[x] f^{\prime}(x) d x, a>1$, where $[x]$ denotes the greatest integer not exceeding $x$ is
1) $a f(a)-\{f(1)+f(2)+\ldots+f([a])\}$
2) $[a] f(a)-\{f(1)+f(2)+\ldots+f([a])\}$
3) $[a] f([a])-\{f(1)+f(2)+\ldots+f(a)\}$
4) $a f([a])-\{f(1)+f(2)+\ldots+f(a)\}$

Solution

As learnt in concept

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$[x]$ has to be split into integral limits.

$\int_1^a[x] f^{\prime}(x) d x$

=$\int_1^2 f^{\prime}(x) d x+\int_2^3 2 f^{\prime}(x) d x+\ldots-\ldots+\int_{[a]}^a[a] f^{\prime}(x) d x$

$\begin{aligned} & f(2)-f(1)+2 f(3)-2 f(2)+--------------- \\ = & ---------+[a] f(a)-[a] f([a])\end{aligned}$

Terms start cancelling out,

We get,

$\begin{aligned} & -f(1)-f(2)-f(3)------------------- \\ - & ---f[a]+[a] f(a)\end{aligned}$

=$=[a] f(a)-(f(1)+f(2)+\cdots-\cdots-\cdots-\cdots-\cdots([a])$

Example 3: $\int_0^{\sqrt{2}}\left[x^2\right] d x$ is

1) $2-\sqrt{2}$
2) $2+\sqrt{2}$
3) $\sqrt{2}-$
4) $\sqrt{2}-2$

Solution

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$\begin{aligned} & \int_0^2\left[x^2\right] d x=\int_0^1\left[x^2\right] d x+\int_1^{\sqrt{2}}\left[x^2\right] d x \\ & \Rightarrow 0+\int_1^{\sqrt{2}} 1 d x=\sqrt{2}-1\end{aligned}$

Example 4: Choose the correct option?

1) $\int_{-a}^a f(x) d x=\int_{-a}^0 f(x) d x+\int_0^a f(x) d x$
2) $\int_a^c f(x) d x=\int_a^d f(x) d x+\int_d^c f(x) d x$; where $a<d<c$
3) $\int_a^c f(x) d x=\int_a^b f(x) d x+\int_b^c f(x) d x$; where $a<c<b$

4) All are true.

Solution

As we have learnt,

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

It doesn't matter if b lies between a and c or not.

Example 5: The value of the integral $\int_{-2}^2 \frac{\sin ^2 x}{\left[\frac{x}{\pi}\right]+\frac{1}{2}} d x$(where $[x]$ denotes the greatest integer less than or equal to (x) ) is :

1) $\sin 4$

2) 0

3) 4

4) $4-\sin 4$

Solution

Fundamental Properties of Definite integration -

If the function is continuous in (a, b ) then integration of a function a to b will be same as the sum of integrals of the same function from a to c and c to b.

$\int_b^a f(x) d x=\int_a^c f(x) d x+\int_c^b f(x) d x$

- wherein

$\begin{aligned} & I=\int_2^{-2} \frac{\sin ^2 x}{\left|\frac{1}{7}\right|+\frac{1}{2}} d x \\ & =\int_2^0 \frac{\sin ^2 x}{\frac{1}{2}} d x+\int_0^{-2} \frac{\sin ^2 x}{-1+\frac{1}{2}} d x \\ & 2 \oint_2^0 \sin ^2 x d x 1-2 \int_0^{-2} \sin ^2 x d x \\ & P u t x=-p \Rightarrow d x=-d y \sin ^2(-p)=\sin ^2 p \\ & =2 \oint_0^2 \sin ^2 x d x+2 \int_2^0 \sin ^2 P d p\end{aligned}$

List of Topics Related to Definite Integrals of Piecewise Functions

Explore essential topics linked to definite integrals of piecewise functions, including applications of integrals, integrals of particular functions, indefinite integrals, integration by parts, and inequalities in definite integration. Exploring these areas will deepen your understanding of integrating complex, multi-condition functions across given intervals.

Application of Integrals

Integral of Particular Functions

Indefinite Integrals

Integration by parts

Application of Inequality in Definite Integration

NCERT Resources

Access comprehensive NCERT resources for Class 12 Maths Chapter 7 on Integrals, including well-structured notes, detailed solutions, and exemplar problem sets. These materials are expertly curated to aid conceptual clarity and strengthen exam readiness.

NCERT Class 12 Maths Notes for Chapter 7 - Integrals

NCERT Class 12 Maths Solutions for Chapter 7 - Integrals

NCERT Class 12 Maths Exemplar Solutions for Chapter 7 - Integrals

Practice Questions based on Definite Integrals of Piecewise Functions

Enhance your understanding of definite integrals involving piecewise functions with these targeted practice questions. These exercises help build skills in handling integration across different function segments and improve problem-solving accuracy.

Piecewise Definite Integration- Practice Question MCQ

We have provided below the practice questions related to different concepts of integration to improve your understanding: