Quadratic Equation in two Variables - Definition, Formulas and Examples

A quadratic equation is a second-order polynomial equation in a single variable. It is a second-degree algebraic expression and is of the form $a x^2+b x+c=0$. The term "quadratic" comes from the Latin word "quadratus" meaning square, which refers to the fact that the variable x is squared in the equation. In other words, a quadratic equation is an "equation of degree 2. ." There are many scenarios where a quadratic equation is used. Further, a quadratic equation has numerous applications in physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.

Quadratic equation

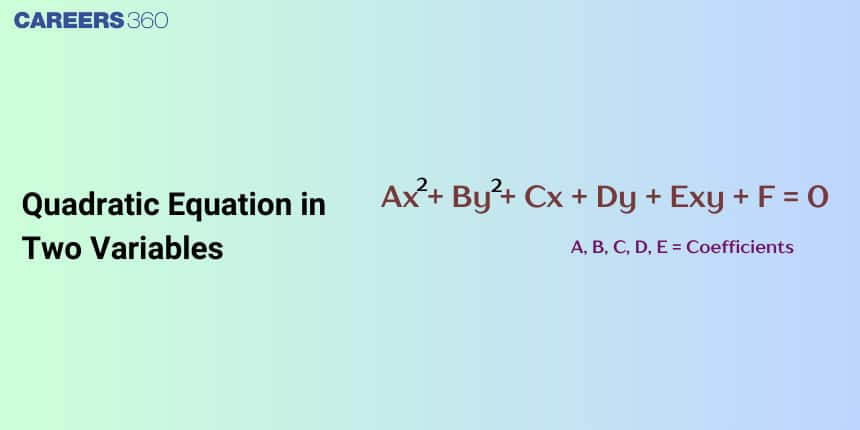
A polynomial equation in which the highest degree of a variable term is 2 is called a quadratic equation.

Standard form of the quadratic equation is $a x^2+b x+c=0$
Where $\mathrm{a}, \mathrm{b}$, and c are constants (they may be real or imaginary) and called the coefficients of the equation and $a \neq 0$ ( a is also called the leading coefficient).

Example: $5 x^2-3 x+2=0, x^2=0,(1+i) x^2-3 x+2 i=0
$

As the degree of the quadratic polynomial is 2, so it always has 2 roots (number of real roots + number of imaginary roots $=2$ )

Quadratic equation in two variable

The general quadratic equation $a x^2+2 h x y+b y^2+2 g x+2 f y+c=0$ can be resolved into linear factors

$
a x^2+2 h x y+b y^2+2 g x+2 f y+c=0
$

we can write,

$
a x^2+2(h y+g) x+\left(b y^2+2 f y+c\right)=0
$

equation (ii) is quadratic form in terms of $x$
using the formula to get roots of quadratic equation

$
\begin{aligned}
& \therefore \mathrm{x}=\frac{-2(\mathrm{hy}+g) \pm \sqrt{4(\mathrm{hy}+g)^2-4 \mathrm{a}\left(\mathrm{by}^2+2 \mathrm{fy}+\mathrm{c}\right)}}{2 \mathrm{a}} \\
& \Rightarrow \mathrm{x}=\frac{-(\mathrm{hy}+\mathrm{g}) \pm \sqrt{\mathrm{h}^2 \mathrm{y}^2+2 g h y+g^2-\mathrm{aby}^2-\mathrm{a} 2 f \mathrm{y}-\mathrm{ac}}}{\mathrm{a}} \\
& \Rightarrow \mathrm{ax}+\mathrm{hy}+g= \pm \sqrt{\mathrm{h}^2 \mathrm{y}^2+2 g h \mathrm{~g}+\mathrm{g}^2-\mathrm{aby}-\mathrm{a} 2 \mathrm{fy}-\mathrm{ac}} \\
& \Rightarrow a x+h y+g= \pm \sqrt{\left(h^2-a b\right) y^2+2(g h-a f) y+g^2-a c}
\end{aligned}
$

The expression (i) can be resolved into linear factors if

$
\left(h^2-a b\right) y^2+2(g h-a f) y+g^2-a c \text { is a perfect square and } \mathrm{h}^2-a b>0
$

The conditions for which $\left(h^2-a b\right) y^2+2(g h-a f) y+g^2-a c$ will be perfect square when $4(\mathrm{gh}-\mathrm{af})^2-4\left(\mathrm{~h}^2-\mathrm{ab}\right)\left(\mathrm{g}^2-\mathrm{ac}\right)=0 \quad\left[\mathrm{D}=\mathrm{b}^2-4 \mathrm{ac}=0\right.$, for perfact square $]$ $\Rightarrow \mathrm{g}^2 \mathrm{~h}^2-2 g h a f+\mathrm{a}^2 \mathrm{f}^2-\mathrm{h}^2 \mathrm{~g}^2+\mathrm{h}^2 \mathrm{ac}+\mathrm{abg}^2-\mathrm{a}^2 \mathrm{bc}=0$
$\Rightarrow \mathrm{abc}+2 \mathrm{fgh}-\mathrm{af}^2-\mathrm{bg}^2-\mathrm{ch}^2=0$

Conics based on the discriminant \(\Delta\) of the conic section.

1. Discriminant of a Conic Section: For a quadratic equation in two variables, the discriminant \(\Delta\) is given by:
$ \Delta = b^2 - 4ac $

2.Conditions Based on \(\Delta\):

Circle:When \(\Delta < 0\) and \(a = c\), the equation represents a circle.
This is because the cross term \(bxy\) is absent, and the quadratic terms are equal.

Ellipse: When \(\Delta < 0\) and \(a \neq c\), the equation represents an ellipse.
The discriminant is negative, indicating a shape that is always closed.

Parabola: When \(\Delta = 0\), the equation represents a parabola.
This occurs when the discriminant is zero, which means there is only one line of symmetry.

Hyperbola: When \(\Delta > 0\), the equation represents a hyperbola. A positive discriminant indicates that the conic section is open and consists of two distinct curves.

Factors of Solving Quadratic Equations

Generally, a quadratic equation can be written in the form of ${a x}^2+b x+c=0$ where the value of $a$ is considered the equivalent to zero. Based on these equations, several factors are used to find the solution of the quadratic equation that is mentioned below:
- By pulling all the terms on any one side of the equal sign
- By setting each factor equal to zero
- By solving each of the separate equations one can get.

Summary

It can be stated that this study has focussed on representing the quadratic equation in two variables. It has been found in the discussion section that the two variables of the quadratic equation can be $x$ and $y$. The values of these two variables of the equation can be determined by the discriminant. On the other hand, the study further included information regarding the ways of graphing a quadratic expression as well as displaying in-depth knowledge.

Recommend Video;

Solved Examples based on Quadratic Equations with 2 Variables

Example1: The equation $x^2 + y^2 - 4x - 6y + 9 = 0$ represents a

1. Ellipse

2. Circle

3. Parabola

4. Hyperbola

Solution:

$x^2 + y^2 - 4x - 6y + 9 = 0$

Adding and subtracting $4, $

$ (x^2 - 4x + 4-4) + (y^2 - 6y + 9)=0$

$(x^2 - 4x + 4) + (y^2 - 6y + 9) = 4 $

$(x - 2)^2 + (y - 3)^2 = 4$

Comparing it with the general equation of the conics, it is similar to the equation of circle $(x - a)^2 + (y - b)^2 = r^2$

$\therefore$ This equation represents a circle.

The answer is option (2).

Example 2: Solve of the quadratic equations $x^2+y^2=25$ and $x^2-y^2=9$.

Solution:

Adding the equations,

$
\begin{aligned}
\left(x^2+y^2\right)+\left(x^2-y^2\right)=25+9 \\
2 x^2=34 \quad \Rightarrow \quad x^2=17 \quad \Rightarrow \quad x= \pm \sqrt{17}
\end{aligned}
$

Substitute $x^2 = 17$ in $x^2+y^2=25$ :

$
17+y^2=25 \quad \Rightarrow \quad y^2=8 \quad \Rightarrow \quad y= \pm \sqrt{8}= \pm 2 \sqrt{2}
$

The possible values of $x$ and $y$ are

$
(\sqrt{17}, 2 \sqrt{2}), \quad(\sqrt{17},-2 \sqrt{2}), \quad(-\sqrt{17}, 2 \sqrt{2}), \quad(-\sqrt{17},-2 \sqrt{2})
$

Example 3: Check whether $(2,-1)$ is a root of the quadratic equation $3 x^2-2 x y+y^2-7 x+$ $5 y-2=0$.

Solution:
Substitute $(2,-1)$ in the equation:

$
\begin{gathered}
3(2)^2-2(2)(-1)+(-1)^2-7(2)+5(-1)-2 \\
=12+4+1-14-5-2 \\
=12+4+1-14-5-2=-4
\end{gathered}
$

The equation does not equal $0$ , so the point $(2,-1)$ is not the root of the equation.

Example 4: Find the roots for the quadratic equation $4 x^2+8 x-9 y^2-12 y+4=0 $

Solution:
$
4 x^2+8 x-9 y^2-12 y+4=0 $

$4\left(x^2+2 x\right)-9\left(y^2+\frac{4}{3} y\right)=-4 $

$4\left(x^2+2 x+1-1\right)-9\left(y^2+\frac{4}{3} y+\frac{4}{9}-\frac{4}{9}\right)=-4 $

$4\left((x+1)^2-1\right)-9\left(\left(y+\frac{2}{3}\right)^2-\frac{4}{9}\right)=-4$

$4(x+1)^2-4-9\left(y+\frac{2}{3}\right)^2+4=-4 $

$4(x+1)^2-9\left(y+\frac{2}{3}\right)^2=-4 $

$\frac{(x+1)^2}{1}-\frac{\left(y+\frac{2}{3}\right)^2}{\frac{4}{9}}=1
$

This represents a hyperbola centered at $\left(-1,-\frac{2}{3}\right)$.

So, $\left(-1,-\frac{2}{3}\right)$ is one the of the root of the equation $4 x^2+8 x-9 y^2-12 y+4=0 $.

Example 5:

The quadratic equation $4 x^ 2+9 y^ 2-36=0$ represents a

Solution:
$4 x^2+9 y^2-36=0$
$4 x^ 2 / 36+9 y^ 2 / 36=1$ $x^ 2 / 9+y^ 2 / 4=1$
This represents the equation of an ellipse with semi-major axis $3$ and semiminor axis $2$ .
$\Delta=b^ 2-4 a c=0^ 2-4 * 4 * 9=-144$
Since $\Delta<0$ and a $\neq c$, this confirms that this equation is an ellipse.