Dragos Rule
How do we predict the stability and geometry of covalent hydrides? Why are some hydrides stable and while others are unstable and decompose easily? We will get these answers by studying Drago's rule. Drago’s Rule helps in understanding the bonding in hydrides of Group 13 and 14 elements, particularly in predicting whether $d\pi-p \pi$ bonding or back-donation will occur or not.
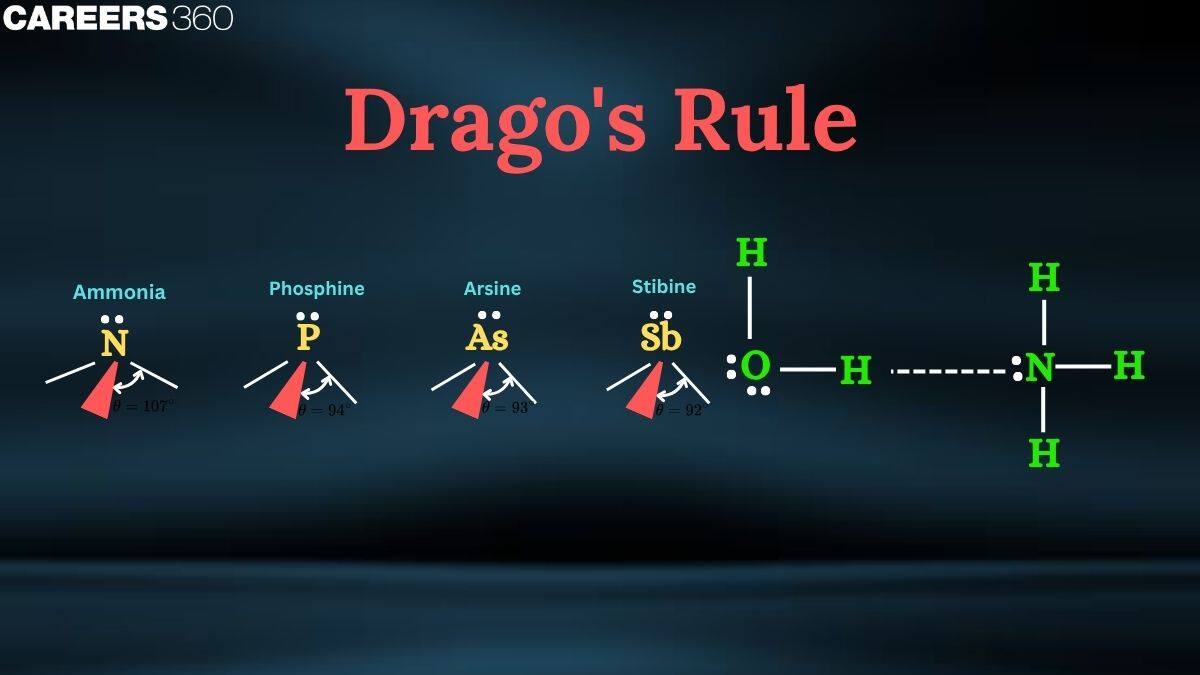
Drago's rule is an empirically based concept applied with an understanding of bond angles and molecular geometries of some hydrides; particularly, those that contain the elements of groups 15 and 16 from the periodic table are considered. This is admitted to include elements in the third period and lower, like phosphorus, arsenic, antimony, sulfur, selenium, and tellurium.
In this article, we will cover the concept of Drago's Rule. This concept falls under the broader category of Chemical Bonding, which is a crucial chapter in Class 11 chemistry. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more.
Also Read -
Drago's Rule
Drago’s Rule is a principle in inorganic chemistry used to predict the bonding behavior of hydrides, particularly of Group 13 (B, Al, Ga) and Group 14 (C, Si, Ge, etc.) elements. Dragos rule explains the bond angles of hydrides of groups 14, 15, and 16 and 2nd members of each of these three groups.
According to Drago's rule, if the central atom is less electronegative and has a low tendency to form multiple bonds, and the hydrogen atoms are not strongly electronegative, then the hybridization of the central atom is not necessary for bond formation. Instead, the bonds are formed using pure atomic orbitals without mixing.
In Drago’s rule, when the various conditions are satisfied as mentioned below, then the energy difference will be very high between the participating atomic orbitals, and hence no mixing of orbitals or hybridization takes place.
-
At least one lone pair must be present on the central atom.
-
The central atom must be off or below the 3rd period.
-
The electronegativity of the surrounding atoms must be less than or equal to 2.1.
-
For these hydrides, hybridization does not take place, and thus bonding takes place only through pure atomic p orbitals, like in PH3, and hence the bond angle will be approximately $90^0$.
For example, the bond angle for $\mathrm{H}_2 \mathrm{O}$ is 104.50 but for $\mathrm{S}_2 \mathrm{H}, \mathrm{Se}_2 \mathrm{H}$, and $\mathrm{Te}_2 \mathrm{H}$, the bond angles are approximately $90^0$.
Also Check-
Conditions and Implications of the Drago Rule
The following must be met for Drago's rule to be valid in a good number of cases:
1. Lone Pairs: The central atom has to contain a lone pair of electrons.
2. Element Group: It has to be a member of groups 13 through 16, be on the third period, and be on.
3. Electronegativity: The centrality of the atom, concerning electronegativity, should be 2.5 or less.
In such cases, the sum of sigma bonds and lone pairs on the central atom becomes four. Hybridization is hence not required, and atomic orbitals may directly participate in bond formation. This leads to odd molecular geometries that do not ideally fall into conventional theories of hybridization.
Important points for Drago's Rule:
Hybridization: When Drago's rule is applicable, the central atom does not hybridize.
Pure Atomic Orbitals: The lone pair remains in a non-hybridized s-orbital, instead of hybrid orbitals, and the bonds are formed by the overlap of pure p-orbitals.
Bond Angles: As the pure p-orbitals are oriented perpendicularly to each other, this results in bond angles that are closer to 90°.
.jpg)
Bond angle is the angle between two bonds that form between two atoms. The figure given below illustrates the concept.

NCERT Chemistry Notes:
Real-Life Applications and Relativity
Drago's rule has a huge impact on describing the behavior of so many molecules in such diverse areas. Take for instance the compound phosphine, PH3. The central phosphorus atom contains a lone pair of electrons. As we all have an idea, it falls under group 15 in the periodic table. In addition, its electronegativity is 2.19. Applying Drago's rule, it could easily be derived that the s-character percent in P-H bonds is less, about 6%. Hence, the lone pair in the compound remains in an orbital that is highly rich in s-character. This is something that never happens in a hybridized orbital. This causes the bond angle to be about 90°, which again deviates from the idealized geometry of a tetrahedron.
Related Topics:
Recommended topic video on (Bond angle and Drago's rule)
Some Solved Examples
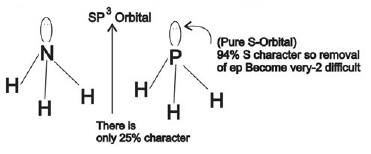
Example 1: Why is NH3 a stronger Lewis base than PH3?
1) In NH3 lone pair is present in one of the sp3 hybridized orbitals, while in PH3 lone pair is present in pure s-orbital.
2) In NH3 lone pair is present in a pure s-orbital, while in PH3 lone pair is present in one of the sp3 hybridized orbitals.
3) In NH3 lone pair is present in one of the sp3d hybridised orbitals, while in PH3 lone pair is present in pure s-orbital
4) None
Solution
In NH3 lone pair is present in one of the sp3 hybridized orbitals, while in PH3 lone pair is present in pure s-orbital.
Hence, the lone pair donation capacity of NH3 is stronger than PH3.
Therefore, option number(1) is correct.
Example 2: As the s-character of a hybridized orbital decreases, the bond angle:
1) Decreases
2) Increases
3) Does not change
4) Becomes zero
Solution
As the s-character of hybridized orbitals decreases, the bond angle also decreases. In sp3 hybridisation: s-character (1/4), bond angle 109°. In sp2 hybridization: s-character (1/3), bond angle 120°. In sp hybridization: s-character (1/2), bond angle 180°.
Hence, the answer is option (1).
Example 3: The HCH bond angle in {HCHO} is nearly equal to:
1) $120^0$
2) $90^{\circ}$
3) $60^0$
4) $ 180^0$
Solution
The hybridization of HCHO is sp2
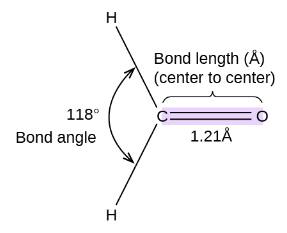
The bond angle in HCHO is close to 120o Facing repulsion by the lone pair of Oxygen.
Hence, option number (1) is correct
Example 4: Which one of the following compounds has the smallest bond angle in its molecule?
1) $\mathrm{SO}_2$
2) $\mathrm{OH}_2 $
3) $\left(\mathrm{SH}_2\right)$
4) $\mathrm{NH}_3 $
Solution:
The repulsion force acts on bonds due to a lone pair present on the central atom, then the bond angle between multiple bonds decreases.
As the number of lone pairs increases bond angle decreases.
As the size of the central atom increases and lone pairs are also present then the bond angle decreases more.
| Molecule | Bond angle | Number of Lone pairs |
| $\mathrm{SO}_2$ | $119.5^0$ | 1 |
| $\mathrm{H}_2 \mathrm{O}$ | $104.5^0$ | 2 |
| $\mathrm{H}_2 \mathrm{S}$ | $92.5^0$ | 2 |
| $\mathrm{NH}_3$ | $107^0$ | 1 |
O and S have two lone pair.
Atom size S > O
So, $\mathrm{H}_2 \mathrm{S}$has the smallest bond angle.
Hence, the answer is the option (3).
Example 5: The dipole moments of CCl4, CHCl3 and CH4 are in the order:
1) $\mathrm{CH}_4=\mathrm{CCl}_4<\mathrm{CHCl}_3$
2) $\mathrm{CHCl}_3<\mathrm{CH}_4=\mathrm{CCl}_4$
3) $\mathrm{CH}_4<\mathrm{CCl}_4<\mathrm{CHCl}_3$
4) $\mathrm{CCl}_4<\mathrm{CH}_4<\mathrm{CHCl}_3$
Solution
Let us first look at the structures of the given compounds
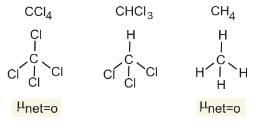
Clearly $\mu \neq 0$ of $\mathrm{CHCl}_3$
Therefore, Option(1) is correct.
$\mathrm{CH}_4=\mathrm{CCl}_4<\mathrm{CHCl}_3$
Example 6:
Given below are two statements:
Statement - I : Since Fluorine is more electronegative than nitrogen, the net dipole moment of $\mathrm{NF}_3$ is greater than $\mathrm{NH}_3$.
Statement - II : In $\mathrm{NH}_3$, the orbital dipole due to lone pair and the dipole moment of NH bonds are in opposite direction, but in $\mathrm{NF}_3$ the orbital dipole due to lone pair and dipole moments of $\mathrm{N}-\mathrm{F}$ bonds are in same direction.
In the light of the above statements, choose the most appropriate from the options given below: [JEE Main 2024]
1) Statement I is true but Statement II is false.
2) Both Statement I and Statement II are false.
3) Both Statement I and Statement II are true.
4) Statement I is false but Statement II is true.
Solution:
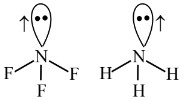
Both statement are false.
Hence, the answer is the option (2).
Practice More Questions with the Link Given Below:
Conclusion
In a nutshell, one such principle that aids inorganic chemistry in obtaining knowledge about molecular geometries and bond angles of certain hydride molecules is Drago's rule. Therefore, it can be done that much predictions and explanations of the behavior of these molecules under different contexts by the chemist, based on an understanding of the conditions under which this rule operates and its implications.
Frequently Asked Questions (FAQs)
If substituents are highly electronegative, the energy gap might be smaller and mixing/hybridization could become favorable. In such cases, Drago’s Rule might not apply cleanly or may break down.
It doesn’t completely discard those models, but rather gives an exception. Drago’s Rule is empirical: it points out cases where the energy differences are so large that hybridization is unfavorable. Some criticize it as a “rule of thumb” rather than a rigorous quantum mechanical derivation.
- PH₃ (phosphine) — P is period 3, has a lone pair, bonded to H (low EN). Bond angle ~93°.
- H₂S, H₂Se — central atoms S, Se etc. with lone pairs and bonding to H; they tend to show smaller angles than predicted by ideal hybridization.
- It helps explain why compounds like PH₃ (phosphine) have unusually small bond angles (~ 93°) rather than what VSEPR or ideal hybridization might predict.
- It accounts for the fact that the lone pair does not mix into hybrid orbitals (i.e. it remains in s‑character) in certain heavier p‑block hydrides. This leads to bonding via pure p orbitals, which are orthogonal, pushing bond angles toward ~90°.
- It provides a rationale for why heavier hydrides are weaker bases compared to lighter analogues (because the lone pair is in an s orbital and less available for protonation).
- Use it as a shortcut to predict which compounds will show “near 90°” bond angles instead of ideal tetrahedral angles when dealing with heavier hydrides.
- Recognize which molecules fall under its criteria (central atom from period 3 or below, lone pair, substituents of low EN).
- Compare predictions from Drago’s Rule with standard hybridization / VSEPR and see which is more reasonable in that context.
