Definite Integral - Calculus

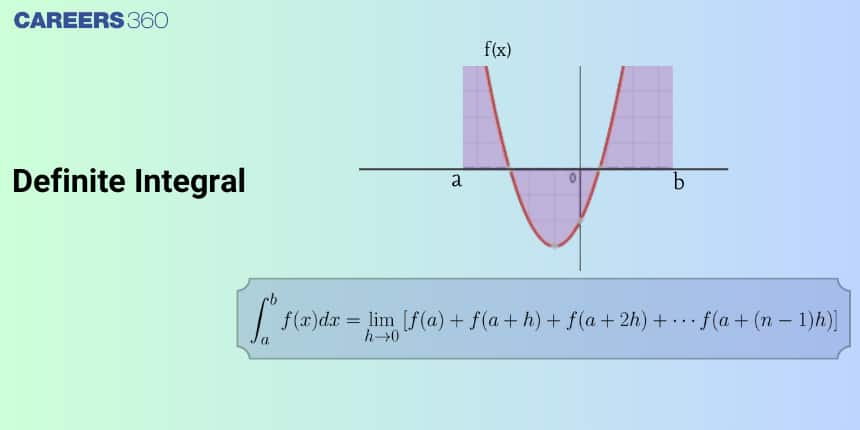
Definite integral as the limit of a sum (Area under the curve)

Definite integration calculates the area under a curve between two specific points on the x-axis.

Let f be a function of x defined on the closed interval [a, b] and F be another function such that $\frac{d}{d x}(F(x))=f(x)$ for all x in the domain of f, then

$\int_a^b f(x) d x=[F(x)+c]_a^b=F(b)-F(a)$is called the definite integral of the function f(x) over the interval [a, b], where a is called the lower limit of the integral and b is called the upper limit of the integral.

Let f(x) be a continuous real-valued function defined on the closed interval [a, b] which is divided into n parts as shown in the figure.

Each subinterval denoted as $\left[x_0, x_1\right],\left[x_1, x_2\right], \ldots\left[x_{i-1}, x_i\right], \ldots,\left[x_{n-1}, x_n\right]$ having equal width $\frac{b-a}{n}$ where, $x_0=a$ and $x_n=b$.

$
\Rightarrow \quad x_i-x_{i-1}=\frac{b-a}{n} \quad \text { for } i=1,2,3, \ldots, n
$
We denote the width of each subinterval with the notation $\Delta x$, so $\quad \Delta x=\frac{b-a}{n}$ and $x_i=x_0+i \Delta x$

On each subinterval,$\left.x_{i-1}, x_i\right]$ (for $\left.i=1,2,3, \ldots, n\right)$ a rectangle is constructed with width Δx and height equal to$f\left(x_{i-1}\right)$ which is the function value at the left endpoint of the subinterval. Then the area of this rectangle is s $f\left(x_{i-1}\right) \Delta x$. Adding the areas of all these rectangles, we get an approximate value for A

$\begin{aligned} A \approx L_n & =f\left(x_0\right) \Delta x+f\left(x_1\right) \Delta x+\cdots+f\left(x_{n-1}\right) \Delta x \\ & =\sum_{i=1}^n f\left(x_{i-1}\right) \Delta x\end{aligned}$

$\mathrm{L}_n$ to denote that this is a left-endpoint approximation of A using n subintervals.

The second method for approximating the area under a curve is the right-endpoint approximation. It is almost the same as the left-endpoint approximation, but now the heights of the rectangles are determined by the function values at the right of each subinterval.

This time the height of the rectangle is determined by the function value f(xi) at the right endpoint of the subinterval. Then, the area of each rectangle is f(xi)Δx and the approximation for A is given by

$\begin{aligned} A \approx R_n & =f\left(x_1\right) \Delta x+f\left(x_2\right) \Delta x+\cdots+f\left(x_n\right) \Delta x \\ & =\sum_{i=1}^n f\left(x_i\right) \Delta x\end{aligned}$

As $\mathrm{n} \rightarrow \infty$ strips become narrower and narrower, it is assumed that the limiting values of $L_n$ and $R_n$ are the same in both cases and the common limiting value is the required area under the curve.

Symbolically, we write

$\begin{aligned} & \lim _{n \rightarrow \infty} \mathrm{L}_n=\lim _{n \rightarrow \infty} \mathrm{R}_{\mathrm{n}}=\text { area of the region }=\int_a^b f(x) d x \\ & \int_a^b f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^n f\left(x_i\right) \Delta x=\lim _{n \rightarrow \infty} \sum_{i=1}^n\left(\frac{b-a}{n}\right) f\left(a+\left(\frac{b-a}{n}\right) i\right) \\ & \text { where, } \quad \Delta x=\frac{b-a}{n} \text { and } x_i=x_0+\Delta x . i\end{aligned}$

NOTE:

1. If $\mathrm{a}=0, \mathrm{~b}=1$, then

$\int_0^1 f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=0}^{n-1} \frac{1}{n} f\left(\frac{i}{n}\right)$

2. From the definition of the definite integral, we have

$\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{i=\varphi(n)}^{\psi(n)} f\left(\frac{i}{n}\right)=\int_a^b f(x) d x$, where
(i) $\quad \Sigma$ is replaced by $\int$ sign
(ii) $\frac{i}{n}$ is replaced by $x$
(iii) $\frac{1}{n}$ is replaced by $d x$
(iv) To obtain the limits of integration, we use $\mathrm{a}=\lim _{\mathrm{n} \rightarrow \infty} \frac{\phi(\mathrm{n})}{\mathrm{n}}$ and $\mathrm{b}=\lim _{\mathrm{n} \rightarrow \infty} \frac{\psi(\mathrm{n})}{\mathrm{n}}$

For example:

$\begin{aligned} & \lim _{n \rightarrow \infty} \sum_{r=1}^{p . n} \frac{1}{n} f\left(\frac{r}{n}\right)=\int_\alpha^\beta f(x) d x \\ & \text { where, } \alpha=\lim _{n \rightarrow \infty} \frac{r}{n}=0(\text { as } r=1) \\ & \text { and } \quad \beta=\lim _{n \rightarrow \infty} \frac{r}{n}=p(\text { as } r=p n)\end{aligned}$

Definite Integrals of Special Functions

When working with definite integrals, certain functions behave in predictable ways that allow us to simplify evaluation using symmetry, periodicity, or functional identities. Many problems in exams exploit these properties to get exact results without performing full integration. Below are key classes of special functions and the techniques commonly used to evaluate their definite integrals.

Definite Integrals Involving Exponential Functions

Exponential functions often appear in integrals of the form
$ \int_a^b e^{kx} f(x),dx $
and can be evaluated using standard identities or reduction-based approaches.

Key results and methods

• Basic form:
  $ \int_a^b e^{kx} dx = \frac{1}{k}(e^{kb} - e^{ka}) $

• Integrals with polynomials:
  Use repeated integration by parts.
  Example:
  $ \int_0^1 x e^x dx = \left[x e^x\right]_0^1 - \int_0^1 e^x dx = e - (e - 1) = 1 $

• Even–odd symmetry:
  For limits $[-a, a]$
  $ e^x $ is neither even nor odd, but
  $ e^x + e^{-x} = 2\cosh x $ (even)
  $ e^x - e^{-x} = 2\sinh x $ (odd)

  Thus:
  $ \int_{-a}^a \sinh x , dx = 0 $

• Standard property:
  $ \int_0^\infty x^n e^{-kx} dx = \frac{n!}{k^{n+1}} $
  Widely used in solving differential equations and probability density integrals.

Definite Integrals Involving Logarithmic Functions

Logarithmic functions often require substitution, symmetry arguments, or special identities.

Key methods and results

• Integral identity:
  $ \int_0^1 \ln x , dx = -1 $

• Power-log integrals:
  $ \int_0^1 x^n \ln x , dx = -\frac{1}{(n+1)^2} $

• Reflection property:
  For many integrals of the form
  $ I = \int_0^1 f(x) \ln(x),dx $
  Using substitution $x = 1 - t$ often simplifies or reveals symmetry.

• Beta function link:
  $ \int_0^1 x^{a-1}(1-x)^{b-1} dx = B(a,b) $
  Differentiating w.r.t. $a$ or $b$ produces logarithmic definite integrals.

Definite Integrals Involving Trigonometric Functions

These integrals frequently use periodicity, symmetry, standard trigonometric identities, and reduction formulas.

Key results and strategies

• Even–odd property:
  Over $[-a,a]$

  • $\sin x$ is odd → $ \int_{-a}^a \sin x dx = 0 $

  • $\cos x$ is even → $ \int_{-a}^a \cos x dx = 2\int_0^a \cos x dx $

• Standard trigonometric integrals:
  $ \int_0^{\pi/2} \sin^n x dx = \int_0^{\pi/2} \cos^n x dx $

• Reduction formula example:
  For even powers:
  $ \int_0^{\pi/2} \sin^{2n} x dx = \frac{(2n-1)!!}{(2n)!!} \cdot \frac{\pi}{2} $

• Symmetry property:
  If $f(x) = f(\pi - x)$, then:
  $ \int_0^\pi f(x) dx = 2\int_0^{\pi/2} f(x) dx $

  Example:
  $ \int_0^\pi \sin x \cos^2 x dx = 2\int_0^{\pi/2} \sin x \cos^2 x dx $

• Definite integrals involving periodic functions:
  A function with period $T$ satisfies
  $ \int_a^{a+T} f(x),dx = \int_0^T f(x),dx $

  This simplifies integrals of $\sin(nx)$, $\cos(nx)$, $e^{inx}$, etc.

Solved Examples Based on Definite integral as the limit of a sum:

Example 1: $\int_0^3\{x\} d x$

1) 2

2) 3/2

3) 4

4) 5

Solution

Definite Integrals as the limit of a sum -

$\int_0^l f(x) d x=\lim _{x \rightarrow \infty} \sum \frac{1}{x} f\left(\frac{r}{x}\right)$

Or

$\int_a^b f(x) d x=\lim _{x \rightarrow \infty} h \sum_{r=0}^x f(a+r h)$

- wherein

Where $f(x)$ is a continuous function in $[0, l]$

Where $h=\frac{b-a}{x}$ And $f(x)$ is continuous in $[a, b]$

$\int_0^3\{x\}=\int_0^1\{x\} d x+\int_1^2\{x\} d x+\int_2^3\{x\} d x$

$=3 / 2$

Example 2: $\lim _{n \rightarrow \infty}\left[\frac{1}{n}+\frac{n}{(n+1)^2}+\frac{n}{(n+2)^2}+\ldots \ldots \ldots \ldots \ldots+\frac{n}{(2 n-1)^2}\right]$ is equal to:

1) $\frac{1}{2}$
2) 1
3) $\frac{1}{3}$
4) $\frac{1}{4}$

Solution

$\lim _{n \rightarrow \infty}\left[\frac{1}{n}+\frac{n}{(n+1)^2}+\frac{n}{(n+2)^2}+\ldots+\frac{n}{(2 n-1)^2}\right]$

$\begin{aligned} & =\lim _{n \rightarrow \infty} \sum_{r=0}^{n-1} \frac{n}{(n+r)^2}=\lim _{n \rightarrow \infty} \sum_{r=0}^{n-1} \frac{n}{n^2+2 n r+r^2} \\ & =\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{r=0}^{n-1} \frac{1}{(r / n)^2+2(r / n)+1}\end{aligned}$

$=\int_0^1 \frac{\mathrm{dx}}{(\mathrm{x}+1)^2}=\left[\frac{-1}{(\mathrm{x}+1)}\right]_0^1=\frac{1}{2}$

Hence, the answer is the option (1).

Example 3: $\left.\lim _{n \rightarrow \infty}\left(\frac{(n+1)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}\right)+\frac{(n+2)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}+\ldots \ldots \ldots+\frac{(2 n)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}\right)$ is equal to:

1) $\frac{3}{4}(2)^{\frac{4}{3}}-\frac{3}{4}$
2) $\frac{4}{3}(2)^{\frac{4}{3}}$
3) $\frac{3}{4}(2)^{\frac{4}{3}}-\frac{4}{3}$
4) $\frac{4}{3}(2)^{\frac{3}{4}}$

Solution

$\lim _{n \rightarrow \infty}\left(\frac{(n+1)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}+\frac{(n+2)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}+\ldots \ldots \ldots \ldots+\frac{(2 n)^{\frac{1}{3}}}{(n)^{\frac{4}{3}}}\right)$

$=\lim _{n \rightarrow \infty} \frac{1}{n}\left[\left(1+\frac{1}{n}\right)^{\frac{1}{3}}+\left(1+\frac{2}{n}\right)^{\frac{1}{3}}+\ldots \ldots \ldots+\left(1+\frac{n}{n}\right)^{\frac{1}{3}}\right]$

$\begin{aligned} & =\frac{1}{n} \sum_{r=1}^n\left(1+\frac{r}{n}\right)^{\frac{1}{3}} \\ & =\int_0^1(1+x)^{\frac{1}{3}} d x=\frac{3}{4}\left(2^{\frac{4}{3}}-1\right)\end{aligned}$

Hence, the answer is option (1).

Example 4: $\lim _{n \rightarrow \infty}\left(\frac{n^2}{\left(n^2+1\right)(n+1)}+\frac{n^2}{\left(n^2+4\right)(n+2)}+\frac{n^2}{\left(n^2+9\right)(n+3)}+\ldots+\frac{n^2}{\left(n^2+n^2\right)(n+n)}\right)$

1) $\frac{\pi}{8}+\frac{1}{4} \log _e 2$
2) $\frac{\pi}{4}+\frac{1}{8} \log _e 2$
3) $\frac{\pi}{4}-\frac{1}{8} \log _{\mathrm{e}} 2$
4) $\frac{\pi}{8}+\log _c \sqrt{2}$

Solution:

$\lim _{n \rightarrow \infty}\left(\frac{n^2}{\left(n^2+1\right)(n+1)}+\frac{n^2}{\left(n^2+4\right)(n+2)}+\cdots+\frac{n^2}{\left(n^2+n^2\right)(n+n)}\right)$

$=\lim _{n \rightarrow \infty} \sum_{r=1}^n \frac{n^2}{\left(n^2+r^2\right)(n+r)}$

$=\int_0^1 \frac{1}{\left(1+x^2\right)(1+x)} d x$

$\begin{aligned} & =\frac{1}{2} \int_0^1 \frac{1}{1+x} d x+\frac{1}{2} \int_b^1 \frac{d x}{1+x^2}-\frac{1}{4} \int_0^1 \frac{2 x}{\left(1+x^2\right)} d x \\ & =\frac{1}{2}[\ln (1+x)]_0^1+\frac{1}{2}\left[\tan ^{-1} x\right]_0^1-\frac{1}{4}\left[\ln \left(1+x^2\right)\right]_0^1 \\ & =\frac{1}{2} \ln 2+\frac{\pi}{8}-\frac{1}{4} \ln 2 \\ & =\frac{\pi}{8}+\frac{1}{4} \log e^2\end{aligned}$

Hence, the answer is the option (1).

Example 5: If $\lim _{n \rightarrow \infty} \frac{(n+1)^{k-1}}{n^{k+1}}[(n k+1)+(n k+2)+\ldots+(n k+n)$$=33 \cdot \lim _{n \rightarrow \infty} \frac{1}{n^{k+1}} \cdot\left[1^k+2^k+3^k+\ldots+n^k\right]$,

then the integral value of $k$ is equal to _______.

1) 5

2) 9

3) 8

4) 6

Solution

$\lim _{n \rightarrow \infty} \frac{(n+1)^{k-1}}{n k+1}[n k \cdot n+1+2+\cdots+n]$

$=\lim _{\mathrm{n} \rightarrow \infty} \frac{(\mathrm{n}+1)^{\mathrm{k}-1}}{\mathrm{n}^{\mathrm{k}+1}} \cdot\left[\mathrm{n}^2 \mathrm{k}+\frac{(\mathrm{n}(\mathrm{n}+1)}{2}\right]$

$\lim _{n \rightarrow \infty} \frac{(n+1)^{k-1} \cdot n^2\left(k+\frac{\left(1+\frac{1}{n}\right)}{2}\right)}{n k+1}$

$\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)\left(k+\frac{\left(1+\frac{1}{n}\right)}{2}\right)$

$\Rightarrow\left(k+\frac{1}{2}\right)$

RHS

$\Rightarrow \lim _{\mathrm{n} \rightarrow \infty} \frac{1}{\mathrm{nk}+1}\left(1^{\mathrm{k}}+2^{\mathrm{k}}+\cdots+\mathrm{h}^{\mathrm{k}}\right)=\frac{1}{\mathrm{k}+1}$

LHS=RHS

$\Rightarrow \mathrm{k}+\frac{1}{2}=33 \cdot \frac{1}{\mathrm{k}+1}$

$\begin{aligned} & \Rightarrow(2 k+1)(k+1)=66 \\ & \Rightarrow(k-5)(2 k+13)=0 \\ & \Rightarrow k=5 \text { or } \frac{13}{9}\end{aligned}$

Hence, the answer is the (5).

List of Topics Related to the Definite Integral

This section presents a curated list of interconnected topics related to definite integrals, covering foundational and advanced concepts in integral calculus. It includes practical applications of integrals, integration of particular functions, indefinite integrals, integration by parts, and the use of inequalities in definite integration.

Application of Integrals

Integral of Particular Functions

Indefinite Integrals

Integration by parts

Application of Inequality in Definite Integration

NCERT Resources

This section gathers all essential NCERT resources for Class 12 Chapter 7 – Integrals, providing comprehensive study support for effective learning and exam preparation. It includes detailed notes, step-by-step solutions, and exemplar problems covering key integration methods such as substitution, partial fractions, and integration by parts.

NCERT Class 12 Maths Notes for Chapter 7 - Integrals

NCERT Class 12 Maths Solutions for Chapter 7 - Integrals

NCERT Class 12 Maths Exemplar Solutions for Chapter 7 - Integrals

Practice Questions based on Definite Integral

This section offers a comprehensive set of practice questions focused on definite integrals, designed to help you strengthen your understanding through applied problem-solving. These exercises cover a variety of functions and integration techniques, including algebraic, trigonometric, and logarithmic forms, enhancing your ability to evaluate definite integrals confidently for both board exams and competitive tests.

Definite Integral Calculus- Practice Question MCQ

We have provided below the practice questions related to different concepts of integration to improve your understanding: