Quadratic Logarithmic Equations

Logarithmic equations are a fundamental aspect of algebra and are widely used in various scientific and engineering fields. Sometimes, logarithmic equations can be transformed into a quadratic form, enabling the use of techniques from quadratic equations to solve them. Logarithmic equations can be expressed in quadratic form, exploring their properties, solution methods, and applications.

This Story also Contains

1. Logarithmic Equations in Quadratic form
2. Summary
3. Solved Examples Based on Logarithmic Equations in Quadratic form

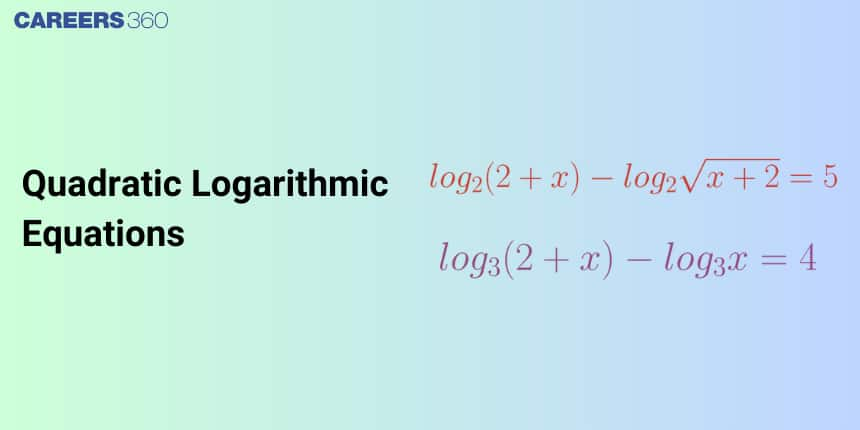
Logarithmic Equations in Quadratic form

A polynomial equation in which the highest degree of a variable term is 2 is called a quadratic equation.

Standard form of a quadratic equation is $a x^2+b x+c=0$

Where a, b, and c are constants (they may be real or imaginary) and called the coefficients of the equation and $a \neq 0$ (a is also called the leading coefficient).

Eg, $-5 x^2-3 x+2=0, x^2=0,(1+i) x^2-3 x+2 i=0$

As the degree of the quadratic polynomial is 2, so it always has 2 roots (number of real roots + number of imaginary roots = 2)

Roots of quadratic equation

The root of the quadratic equation is given by the formula:

$\begin{aligned} & x=\frac{-b \pm \sqrt{D}}{2 a} \\ & \text { or } \\ & x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\end{aligned}$

Where D is called the discriminant of the quadratic equation, given by $D=b^2-4 a c$

Logarithmic Equations:

Equation of the form $\log _{\mathrm{a}} \mathrm{f}(\mathrm{x})=\mathrm{b}(\mathrm{a}>0, \mathrm{a} \neq 1)$, is known as logarithmic equation.
this is equivalent to the equation $\mathrm{f}(\mathrm{x})=\mathrm{a}^{\mathrm{b}}(\mathrm{f}(\mathrm{x})>0)$

Let us see one example to understand

Suppose given equation is $\log _{\log _4 x} 4=2$
base of $\log$ is greater then 0 and not equal to 1
so, $\log _4 x>0$ and $\log _4 x \neq 1$
$x>1$ and $x \neq 4$
now, using $\log _a f(x)=b \Rightarrow f(x)=a^b$

$
\begin{aligned}
& \Rightarrow 4=2^{\log _4 x} \Rightarrow 2^2=2^{\log _4 x} \\
& \Rightarrow 2=\log _4 x \Rightarrow x=4^2 \\
& x=16
\end{aligned}
$

If the given equation is in the form of $f\left(\log _a x\right)=0$, where $a>0$ and $a$ is not equal to 1 . In this case, put $\log _a x=t$ and solve $f(t)=0$.
And if the given equation is in the form of $f\left(\log _x A\right)=0$, where $A>0$. In this case, put $\log _x A=t$ and solve $f(t)=0$.

For example,

Suppose given equation is $\frac{(\log x)^2-4 \log x^2+16}{2-\log x}=0$ given equation can be written as after substituting $t=\log x$

$
\begin{aligned}
& \Rightarrow \frac{t^2-8 \mathrm{t}+16}{2-\mathrm{t}}=0 \\
& \Rightarrow \frac{(\mathrm{t}-4)(\mathrm{t}-4)}{(2-\mathrm{t})}=0 \\
& \Rightarrow \mathrm{t}=4 \\
& \mathrm{t}=\log \mathrm{x}=4 \\
& \because \log \mathrm{x}=\log _{10} \mathrm{x} \\
& \mathrm{x}=10^4
\end{aligned}
$

Summary

Logarithmic equations in quadratic form present an intriguing intersection of logarithmic and quadratic functions. This approach is not only mathematically elegant but also highly practical, with applications in various fields such as mathematics, economics, physics, and engineering. Understanding and mastering these transformations expand our ability to tackle a broader range of mathematical problems, enhancing both theoretical knowledge and practical problem-solving skills.

Recommended Video Based on Quadratic Logarithmic Equations

Solved Examples Based on Logarithmic Equations in Quadratic form

Example 1: What is the solution of the inequation $\log _{x-3}\left(2\left(x^2-10 x+24\right)\right) \geq \log _{(x-3)}\left(x^2-9\right) ?$?

$\begin{aligned} & \text { 1) } x \in[4, \infty] \\ & \text { 2) } x \in(-\infty,-3) \cup[10+\sqrt{43, \infty} \\ & \text { 3) } x \in[10-\sqrt{43}, \infty] \\ & \text { 4) } x \in[10+\sqrt{43}, \infty]\end{aligned}$

Solution

If the given equation is in the form of$f\left(\log _a x\right)=0$, where $a>0$ and a is not equal to 1.

In this case, put$\log _a x=t$ and solve $f(t)=0$

this inequation is equivalent to:

$
\begin{aligned}
& \left(2\left(x^2-10 x+24\right)\right) \geq\left(x^2-9\right) \\
& x^2-9>0 \\
& x-3>1
\end{aligned}
$

on solving these equation we get

$
x \in[10+\sqrt{43}, \infty)
$

Hence, the answer is the option 4.

Example 2: If for $x \in\left(0, \frac{\pi}{2}\right), \log _{10} \sin x+\log _{10} \cos x=-1$ and $\log _{10}(\sin x+\cos x)=\frac{1}{2}\left(\log _{10} n-1\right), n>0$ then the value of n is equal to:

1) 20

2) 16

3) 9

4) 12

Solution
$
\begin{aligned}
& \mathrm{x} \in\left(0, \frac{\pi}{2}\right) \\
& \log _{10} \sin x+\log _{10} \cos x=-1 \\
& \Rightarrow \quad \log _{10} \sin x \cdot \cos x=-1 \\
& \Rightarrow \quad \sin x \cdot \cos x=\frac{1}{10}
\end{aligned}
$

$\begin{aligned} & \log _{10}(\sin x+\cos x)=\frac{1}{2}\left(\log _{10} n-1\right) \\ & \Rightarrow \quad 2 \log _{10}(\sin x+\cos x)=\left(\log _{10} n-\log _{10}\right) \\ & \Rightarrow \quad(\sin x+\cos x)^2=10^{\left(\log _{10} \frac{n}{10}\right)} \\ & \Rightarrow \quad(\sin x+\cos x)^2=\frac{n}{10}\end{aligned}$

$\begin{aligned} \sin ^2 x+\cos ^2 x+2 \sin x \cdot \cos x & =\frac{n}{10} \\ \Rightarrow 1+\frac{1}{5}=\frac{n}{10} \quad \Rightarrow \quad n & =12\end{aligned}$

Hence, the answer is option 4.

Example 3: Let a complex number $z,|z| \neq 1$ satisfy $\log _{\frac{1}{\sqrt{2}}}\left(\frac{|z|+11}{(|z|-1)^2}\right) \leq 2$ Then, the largest value of |z| is equal to _________.

1) 7

2) 6

3) 5

4) 8

Solution

$\begin{array}{r}\log _{\frac{1}{\sqrt{2}}}\left(\frac{|z|+11}{(|z|-1)^2}\right) \leq 2 \\ \frac{|z|+11}{(|z|-1)^2} \geq \frac{1}{2} \\ 2|z|+22 \geq(|z|-1)^2 \\ 2|z|+22 \geq|z|^2+1-2|z| \\ |z|^2-4|z|-21 \leq 0 \\ (|z|-7)(|z|+3) \leq 0\end{array}$

$|z| \in[-3,7]$

$\therefore \quad$ Largest value of $|z|$ is 7

Hence, the answer is option 1.

Example 4: Solve the equation $2 \log _3 x+\log _3\left(x^2-3\right)=\log _3 0.5+5^{\log _5\left(\log _3 8\right)}$

1) $x=0$
2) $x=-2$
3) $x=2$
4) none of the above

Solution

Using properties of logarithm, this equation can be written as
$
\begin{aligned}
& \log _3 x^2+\log _3\left(x^2-3\right)=\log _3 0.5+\log _3 8 \\
& \log _3\left(x^2 \cdot\left(x^2-3\right)\right)=\log _3(0.5 * 8)
\end{aligned}
$
Now we have same base of $\log$ on both sides, so $\log$ can be removed from both sides

$
\begin{aligned}
& x^2\left(x^2-3\right)=0.5 \cdot 8 \\
& x^2\left(x^2-3\right)=4
\end{aligned}
$

$\begin{aligned} & x^4-3 x^2-4=0 \\ & \text { Let } x^2=t \\ & t^2-3 t-4=0 \\ & (t-4)(t+1)=0 \\ & t=4 \text { or } t=-1 \\ & x^2=4 \text { or } x^2=-1 \\ & x= \pm 2\end{aligned}$

Now check whether x= 2 and x = -2 lie in the domain of the original equation.

For x = -2, the first term in the equation is not defined. So it is rejected.

But for x = 2, all the terms are defined.

So x = 2 is the only answer.

Hence, the answer is the option 3.

Example 5: The number of solutions to the equation $\log _{(x+1)}\left(2 x^2+7 x+5\right)+\log _{(2 x+5)}(x+1)^2-4=0, x>0$ $\begin{aligned} & \log _{(x+1)}\left(2 x^2+7 x+5\right)+\log _{(2 x+5)}(x+1)^2-4=0 \\ \Rightarrow & \log _{(x+1)}((x+1)(2 x+5))+2 \log _{(2 x+5)}(x+1)-4=0\end{aligned}$ is:

1) 1

2) 2

3) 3

4) 4

Solution

$\begin{aligned} & \log _{(x+1)}\left(2 x^2+7 x+5\right)+\log _{(2 x+5)}(x+1)^2-4=0 \\ \Rightarrow & \log _{(x+1)}((x+1)(2 x+5))+2 \log _{(2 x+5)}(x+1)-4=0\end{aligned}$
$
\Rightarrow \log _{(x+1)}(x+1)+\log _{(x+1)}(2 x+5)+2 \log _{(2 x+5)}(x+1)-4=0
$
Let $\log _{(x+1)}(2 x+5)=t \Rightarrow \log _{(2 x+5)}(x+1)=\frac{1}{t}$
$
\Rightarrow \log _{(x+1)}(x+1)+\log _{(x+1)}(2 x+5)+2 \log _{(2 x+5)}(x+1)-4=0
$
Let $\log _{(x+1)}(2 x+5)=t \Rightarrow \log _{(2 x+5)}(x+1)=\frac{1}{t}$

$\begin{aligned} & \Rightarrow \quad 1+t+\frac{2}{t}-4=0 \\ & \Rightarrow \quad t^2-3 t+2=0 \\ & \Rightarrow \quad t=1 \quad \text { or } t=2\end{aligned}$

$\begin{aligned} & \Rightarrow \log _{(x+1)}(2 x+5)=1 \text { or } \log _{(x+1)}(2 x+5)=2 \\ & \Rightarrow 2 x+5=(x+1)^1 \text { or } 2 x+5=(x+1)^2 \\ & \Rightarrow x=-4 \quad \text { or } x^2=4\end{aligned}$

$\Rightarrow x=-4$ or $x=2$ or $x=-2$
Given $x>0 \Rightarrow x=2$

$x=2$ also lies in the domain of all the terms, so it is the answer.

Hence, the answer is the option (1).