Position and Displacement Vectors

Position and Displacement Vectors - A Complete Guide

Edited By Vishal kumar | Updated on Sep 24, 2024 06:38 PM IST

A vector may be an extent that has both magnitude and direction. Vectors allow us to explain the quantities which have both direction and magnitude. For instance velocity, and position. In this article we will discuss about, what is Position? Or definition of position. What is position vector? Define position vector with its formula. How to find Position vector? How can we describe the position of an object? What is displacement vector? Give its formula. We define the position vector as a straight-line possessing one end fixed to an object and therefore the other end attached to a moving point (marked by an arrowhead) and wont to represent the position of the purpose relative to the given object. Since, the point moves, the position vector switches long or in direction, and sometimes both length and direction changes. Are you know, what is Position??? So Now We define Position (Edge) is that the location of the thing (whether it is a person, a ball, or a particle) at a given moment in time. Vector physics vallah is anything which also has direction. A displacement vector is an idea from vectors. It’s a vector. It indicates the direction and distance traveled with a line.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

Position and Displacement Vectors - A Complete Guide

Also check-

What is Position Vector?

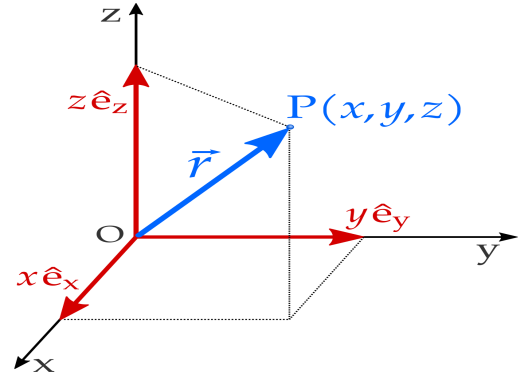
A position or edge(Position) vector, also known as location vector or radius vector, is a Euclidean vector that represents the position of a point P in space in relation to an arbitrary reference origin O. Usually signified as x, r, or s, it point to the straight line segment from O to P.

Radius vector r represent the postion of point P (x, y, z) with repect to origin O

In the above statement, we took a frame of reference to represent your journey from the origin, i.e., your home to succeed in your favorite destinations, first, Tamilnadu, then, Bengluru.
Each destination is marked by an arrow on the graph, which changes or varies as you modify your destination, below represent the same:

Hence, your position vector changes, i.e., twice or twice the length,
So, along the X-axis, the position vector is: ‘i (cap)’ and along the Y-axis, it's ‘j (cap)’. Since the position resultant is represented by r→
, therefore the resultant of the position vectors along with coordinate axes are going to be as follows:

r→ + I (cap) + j (cap) ……………………… (1)

Now In these Articles, the points we have to discuss about Position Vector are:

Explain what's an edge (Position) Vector?
And how to find out the Position Vector?
How can we describe the position of an object?

Often, we've noticed that the vectors start at the origin and terminate at any arbitrary point are referred to as position vectors. These are said to work out the position of some extent with regard to the origin of that time. The orientation/direction of the vectors or the position vector generally points from the origin towards the given point. Within the frame of reference of c\Cartesian if point O is that the origin and Q is a few points that's x1, y1, then the directed position vector from point O to point Q is identified as OQ. Within the space which is three-dimensional if O = (0, 0, and 0) and Q = (x1, y1, z1), then the position vector denoted by r of point Q is represented is:

r = x1i + y1j + z1k

Now let’s suppose that we've two vectors, that are A and B, with position vectors we write a = (2, 4) and b = (3, 5) respectively. We will then write the coordinates of both the vectors that are A and B as:

A = (2, 4), B = (3, 5)

Here before determining the position vector of some extent we first got to determine the coordinates of these particular points. Let’s suppose that we've two points, namely M and N. where the purpose M = (x1, y1) and N = (x2, y2). Next we would like to seek out here the position vector that too from point M to point N the vector MN. To work out this position vector, we simply subtract the corresponding components of M from N:

Written as: MN = (x2-x1, y2-y1)

Related Topics Link,

Position Vector Formula:

If we consider some extent denoted by letter P. Which has the coordinates that are xk, yk within the xy-plane and another point written as Q. Which has the coordinates denoted by xk+1, yk+1.

The formula which is to work out the position vector that's from P to Q is written as:

PQ = ((xk+1)-xk, (yk+1)-yk)

We can now remember the position vector that's PQ which generally refers to a vector that starts at the purpose P and ends at the purpose Q. Similarly if we would like to findout the position vector that's from the purpose Q to the purpose P then we will write:

QP = (xk – (xk+1), yk – (yk+1))

How can we describe the position of an object?

The changes in position of an object with reference to its surroundings during a given interval of your time. An object is moving if its position relative to a hard and fast point is changing. Even things that indicate to be at rest move.

Also Read:

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Displacement Vector

The change within the position vector of an object is understood because the displacement vector. Let us consider an object is at point A at time = 0 and at point B at time = t. The position vectors of the thing at point A and at point B are given as:

Position vector at point A = r^A = 5 i^ + 3 j^+ 4 k^
Position vector at point B = r^B = 2 i^ + 2 j^+ 1 k^
Now, the displacement vector of the thing from interval 0 to t will be:
r^A - r^B = - 3 i^ - j^+ 3k^
The displacement of an object also can be defined because the vector distance between the initial point and therefore the final point. Suppose an object travels from point A to point B within the path shown within the black curve:

The displacement of the particle would be the vector line AB, lead inside the direction A to B. The direction of the displacement vector is usually headed from the initial point to the ultimate point.

Also read -

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. Explain Can an edge(Position) Vector be Negative?

If there are two vectors that are having an equivalent magnitude that's size and therefore the same direction also. Then we will generally call them adequate to one another. A bit like the scalars which may have negative or the positive values. The vectors also can be negative or positive. A vector which is that the negative may be a vector which points within the direction opposite to the reference positive direction.

2. What is meant by Fixed Vector?

Fixed vector is that vector whose initial point or tail is fixed. It's also referred to as localised vector. For instance, The initial point of an edge(position) vector is fixed at the origin of the coordinate axes. So, position vector may be a fixed or localized vector.

3. Explain what's the Position and Displacement Vector?

The vector which is that the position vector is employed to specify the position of a particular body. The term displacement vector is employed to seek out the change that's within the position vector of an object. The vector which generally represents the position of an object and therefore the origin because the frame of reference is understood as position vector.

4. An object has a displacement from position vector

5. What is the meaning of position vector?

Position vector, line having one end fixed to a body and therefore the other end attached to a moving point and wont to describe the position of the purpose relative to the body.