Domain, Co-domain and Range of Function

One of the fundamental ideas in mathematics with a wide range of practical applications is the function. The modeling of large skyscrapers and rapid vehicles alike necessitates the careful application of functions. Functions are used in almost all real-world issue formulation, interpretation, and solution processes.

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

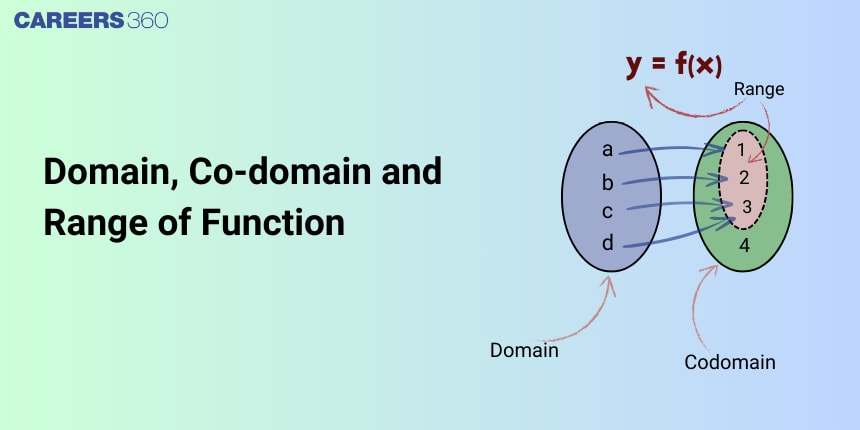
In this article, we will cover the concepts of domain, co-domain, and range of function. This concept falls under the broader category of sets relation and function, a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of seven questions have been asked on this concept, including one in 2019, one in 2021, one in 2022, and four in 2023.

Function

A relation from a set $A$ to a set $B$ is said to be a function from $A$ to $B$ if every element of set $A$ has one and only one image in set $B$.

OR

$A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is said to be a function if each element $x$ in $A$ is assigned a unique element $f(x)$ in $B$, and it is written as $f:A\to B$ and read as $f$ is mapping from $A$ to $B$.

Function

Function

Not a function

Not a function

The third one is not a function because d is not related(mapped) to any element in $B$.

Fourth is not a function as element a in $A$ is mapped to more than one element in $B$.

Formal Definition of a Function

A function relates each element of a set with exactly one element of another set (possibly the same set).

A function relates an input to an output:

Example: This tree grows 20 cm every year, so the height of the tree is related to its age using the function $h$ :

$h(\text{ age })=\text{ age }\times 20$

So, if the age is $10$ years, the height is $h(10)=200\mathrm{cm}$
Saying " $h(10)=200$ " is like saying 10 is related to 200 . Or $10\to 200$

Domain of a function

The collection of all potential values for which a function can be defined is known as its domain or All possible values of $x$ for $f(x)$ is defined $(f(x)$ is a real number) is known as a domain.

If a function is defined from A to B i.e. $\mathrm{f}:\mathrm{A}\to \mathrm{B}$, then all the elements of $\mathrm{set}\mathrm{A}$ is called the Domain of the function.

Let's examine each function's domain in turn.

A set of all real numbers $(R)$ is the domain of any polynomial function, including linear, quadratic, cubic, and so on.
A logarithmic function $f(x)=\log x$ has as its domain $x>0$ or $(0,\mathrm{\infty })$.
A square root function $f(x)=\sqrt{x}$ has as its domain the set of all real numbers that are not negative and are denoted by $[0,\mathrm{\infty }]$.
The set of all real numbers $(R)$ is the domain of an exponential function.

Co-domain of a function

If a function is defined from $A$ to $B$ i.e. $f:A\to B$, then set $B$ is called the Co-domain of the function.

Codomain is the set of the values including the range of the function nd it can have some additional values. The range is the Subset of the Codomain. This is explained using the example,

Given function, $f(x)=\cos x$, such that, $f:R\to R$, then
- Codomain of $f(x)=R$
- Range of $R=(-1,1)$

Range of a function

The set of all possible values of $f(x)$ for every $x$ belonging to the domain is known as the Range of this function.

The set of all possible values of $f(x)$ for every $x$ belonging to the domain is known as the Range of this function.

The range of a function is the set of all the outputs of the function. For any function $f:A\to B$ the sets of values in the $B$ are the range of the function. if $f:A\to B$ is a function such that $f(x)=$ $x^2$ and $A$ is the set of all integers then the range of the function is the set of Range $=\{1,4,9$, $16,\dots \}$. We have to note that the range of the function is the subset of the Co-Domain of the function.

For example, let $A=\{1,2,3,4,5\}$ and $B=\{1,4,8,16,27,64,125\}$. The function $f:A->B$ is defined by $f(x)=x^3$. So here,

Domain: Set $A$

Co-Domain: Set $B$

Range: $\{1,8,27,64,125\}$

The range is always a subset of the co-domain and the Range can be equal to the co-domain in some cases.

How to find the Domain?

• If the domain of $f(x)$ is $A$ and the domain of $g(x)$ is $B$, then the domain of $f(x)+g(x),f(x)-g(x),f(x),g(x)$ is $A\cap B$.
• For the domain of $f(x)/g(x)$, remove values of $x$ for which $g(x)=0$, from $A\cap B$.
• Domain of expressions of type $\mathrm{\$}\mathrm{\setminus }sqrt\{f(x)\}\mathrm{\$}$, we take the common values between $A$ and values of $x$ for which $\mathrm{\$}$ mathrm $\{f\}(\mathrm{lm}$ mathrm $\{x\})\mathrm{lgeq}0\mathrm{\$}$.
• The domain of a polynomial function is $R$.
• Graphical method: we can also find the domain if only the graph of a function is given. We will learn this through the help of solved examples.

Methods to find Range

• For the range of $y=f(x)$, we can first express $x$ as a function of $y:x=g(y)$. Now the domain of $x=g(y)$ is the same as the range of $y=f(x)$
• Graphical method: we can also find the range if only the graph of a function is given.

Note: If only the formula is given, then the co-domain is $R$, and the domain and range have to be found.

• Domain in this case will be all the real values of x for which y is real
• Range is all the real values of $y$ corresponding to values of $x$ in the domain

Recommended Video Related to Domain, Range, and Co-domain of Functions

Solved Examples Based On the Domain, Range, and Co-domain of Functions

Example 1: What is the domain of the function $f(x)=\ln x$ ?
1) $x\equiv R$
2) $x⩾0$
3) $x\in {\mathbb{R}}^{+}$
4) None of these

Solution:
The domain is $x\equiv R^{+}$and here $\ln x$ is not valid for $x=0$ or $x<0$.
Hence, the answer is the option 3.
Example 2: What is the Domain of the function $f(x)=\frac{x^2-4}{x+2}$ ?
1) $x\ne 2$
2) $x\ne -2$
3) $x\ne 0$
4) None of these

Solution:

$f(x)=\frac{x^2-4}{x+2}$
Here x should not be equal to -2, as it makes the denominator value 0.

Hence, the answer is the option 2.

Example 3: For function $f(x)=\tan x$ from $R\to R$. The Co-domain of function is
1) $[-1,1]$
2) $R^{+}$
3) $R$
4) $R^{-}$

Solution:
Co - Domain of function -
All possible outcomes for the function $f(x)$ is known as co-domain unless not specified in question.
When we write $\mathrm{f}:R\to R$
Co - domain $=$ R ; Domain $=\mathrm{R}$.
Hence, the answer is the option 3.
Example 4: In the function $f(x)=\sin xx\in R$ The co-domain of a function is:
1) $(-1,1)$
2) $[-1,1]$
3) $R$
4) not specified.

Solution:

Co - Domain of function -
All possible outcomes for the function $f(x)$ are known as co-domain unless not specified in question.

Since the function is defined for $x\equiv R$.
Domain $=\mathrm{R}$
But co-domain is not specified.
Hence, the answer is the option 4.

Example 5: Find the range of $f(x)=\frac{1}{|x|-x}$
1) $(0,\mathrm{\infty })$
2) $[0,\mathrm{\infty })$
3) $R$
4) None of these

Solution:
For $x\ge 0;|x|=x$
Here $f(x)$ is not defined
For $x<0;|x|=-x$
$f(x)=\frac{1}{-x-x}=-\frac{1}{2x}$

Now as x can only be negative, so f(x) will take all positive values

Hence, the answer is the option 1.