Mathematical Operations: Definition, Questions, Examples

Mathematical operations reasoning questions are an important part of logical reasoning, where symbols and signs are replaced or interchanged to test analytical ability. In logical reasoning, these mathematical operations questions and answers help students strengthen problem-solving skills for competitive exams. Exams like CUET, VITEEE, MAH MBA CET, IPMAT, SSC CGL, SSC CHSL, Bank PO, and other aptitude-based tests frequently include mathematical operations reasoning questions, symbolic operations reasoning questions, and mixed logical puzzles. In this article, we will cover the key concepts, types of problems, solved examples, and tricks to master mathematical operations reasoning effectively. There are various tricks or methods to solve the questions, but the best and the main method to solve these types of questions is the “BODMAS Rule”. BODMAS stands for Brackets, order, division, multiplication, addition and subtraction. With the help of this rule, a student can easily determine the steps to solve a particular equation.

This Story also Contains

1. Types of Questions Based on the Mathematical Operations
2. Recommended Books and Resources for Mathematical Operations
3. Practice Questions based on Mathematical Operations
4. Practice Questions for Interchanging Symbol-Based Questions
5. Practice Questions for Interchanging Symbols and Numbers-Based Questions
6. Verbal Reasoning Topics
7. Practice Questions for Fill-in-the-Blanks-Based Questions
8. Mathematical Operations Questions for SSC/ RRB exams
9. Mathematical Operations Questions for Bank Clerk/ Insurance Assistant exams
10. Common Mistakes in Solving Mathematical Operations Questions
11. Tricks and Shortcuts for Mathematical Operations Reasoning
12. How to Prepare for Mathematical Operations in Competitive Exams
13. Non-Verbal Reasoning Topics

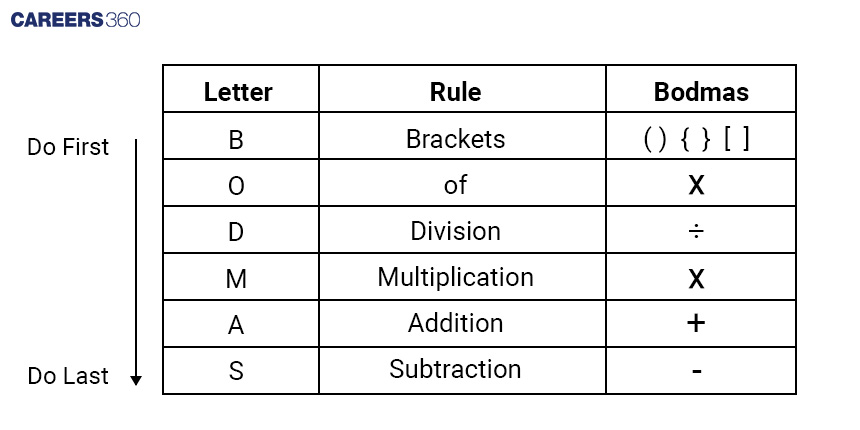
Types of Questions Based on the Mathematical Operations

There are mainly two types of questions that have been seen from mathematical operations -

1. Interchanging Symbol-Based Question
2. Fill in the blanks Based Question

Let’s understand these types with the help of the examples -

1. Interchanging Symbol-Based Question

As it is clear by the word interchange itself, the process of interchanging the place of the elements will be seen in these types of questions. This type of mathematical operation is divided into two parts again -

Interchanging Symbol-Based Questions

In such types of questions, the symbols given in the equation need to be interchanged with the mathematical signs as directed in the question and then solve the obtained equation using the BODMAS rule. Let’s understand this with the help of an example.

Example: If + means ×, – means ÷, ÷ means + and × means –

then, 74 ÷ 11 – 33 + 42 × 16 = ?

1. 64

2. 68

3. 76

4. 72

Answer: In this example, simply interchange the signs as directed in the question. For, + will be interchanged with ×, – will be interchanged with ÷, ÷ will be interchanged with +, and × will be interchanged with –. So, after interchanging, the equation becomes 74 + 11 ÷ 33 × 42 – 16. Now, solve the equation using the BODMAS rule.

= 74 + 11 ÷ 33 × 42 – 16

= 74 + 0.33 × 42 – 16 = 74 + 14 – 16 = 88 – 16 = 72

So, 72 is the required answer to the given equation.

Interchanging Symbols and Numbers-Based Questions

In such types of questions, both the symbols and numbers given in the equation need to be interchanged as directed in the question and then solve the obtained equation using the BODMAS rule. Let’s understand this with the help of an example.

Example: After interchanging the given two numbers and two signs, what will be the value of the equation?

+ and ×, 5 and 4
4 + 6 × 5 – 7 ÷ 1

1. 30

2. 20

3. 27

4. 25

Answer: In this example, simply interchange the signs and numbers as directed in the question. Like, + will be interchanged with ×, and × will be interchanged with +. Also, interchange the numbers as directed. So, after interchanging, the equation becomes 5 × 6 + 4 – 7 ÷ 1, now solve the equation using the BODAMS rule.
= 5 × 6 + 4 – 7 ÷ 1
= 5 × 6 + 4 – 7 = 30 + 4 – 7 = 34 – 7 = 27
So, 27 is the required answer to the given equation.

2. Fill in the blanks-based questions

In these types of questions, an equation is given with a set of numbers and blanks. The equation needs to be completed by filling in the blanks with mathematical signs given in the different options one by one. One of the options will satisfy the equation, resulting in L.H.S. being equal to R.H.S. Let’s understand this with the help of an example.

Example: Select the correct combination of mathematical signs to replace the * signs and balance the given equation sequentially.
65 * 45 * 25 * 5 * 35 * 60

1. −, +, −, +, =

2. +, ×, +, −, =

3. +, −, +, −, =

4. −, +, ÷, +, =

Replace the * symbol with the mathematical signs given in the options one by one and solve the equation using the BODMAS rule. Only option D) satisfies the equation as shown below:

65 − 45 + 25 ÷ 5 + 35 = 60

Solving the L.H.S. of the equation –

= 65 − 45 + 5 + 35

= 105 − 45

= 60

Recommended Books and Resources for Mathematical Operations

1. A Modern Approach to Verbal & Non-Verbal Reasoning by R.S. Aggarwal

2. SSC Reasoning by Rakesh Yadav

3. How to Crack Test of Reasoning by Arihant Publications

4. A New Approach to Reasoning Verbal, Non-Verbal & Analytical by B.S. Sijwali & Indu Sijwali

5. Analytical Reasoning by M.K. Pandey

Question Weightage of Mathematical Operations in Competitive Exams

The number of questions based on mathematical operations varies from exam to exam -

1) Questions asked in SSC exams, i.e. SSC MTS, SSC CGL, SSC CHSL, SSC CPO, Steno - 3 to 4 questions.

2) Questions asked in the Railways exam, i.e. Group D, NTPC, JE, ALP, etc - 2 to 3 questions.

3) Questions asked in Banking exams, Bank PO, Bank Clerk - 3 to 4 questions.

Practice Questions based on Mathematical Operations

The candidates must practice the e-book of mathematical operations and reasoning questions, PDF given below.
Mathematical Operations Questions with Solutions PDF

Practice Questions for Interchanging Symbol-Based Questions

Q1. Directions: What will come in the place of (?) in the following equation, if + and × are interchanged and also – and ÷ are interchanged?

20 ÷ 5 × 10 – 5 + 2 = ?

1. 4

2. 19 (Correct)

3. 12

4. 2

Solution:
Given:
20 ÷ 5 × 10 – 5 + 2 = ?
After interchanging the given mathematical signs, we get –
= 20 – 5 + 10 ÷ 5 × 2
= 20 – 5 + 2 × 2
= 20 – 5 + 4
= 19
So, 19 is the answer to the given equation. Hence, the second option is correct.

Q2. Directions: By interchanging which two signs, the given equation will be correct?

39 – 3 ÷ 13 + 16 × 8 = 17

1. × and – (Correct)

2. + and –

3. ÷ and –

4. × and ÷

Solution:
Given:
39 – 3 ÷ 13 + 16 × 8 = 17
Let's check the options –
First option: × and –
39 – 3 ÷ 13 + 16 × 8 = 17
On interchanging the mathematical signs, we get –
⇒ 39 × 3 ÷ 13 + 16 – 8 = 17
⇒ 9 + 16 – 8
⇒ 25 – 8
⇒ 17
Second option: + and –
39 – 3 ÷ 13 + 16 × 8 = 17
On interchanging the mathematical signs, we get –
⇒ 39 + 3 ÷ 13 – 16 × 8 = 17
⇒ 39 + 0.23 – 16 × 8
⇒ 39 + 0.23 – 128
⇒ – 88.77 ≠ 17
Third option: ÷ and –
39 – 3 ÷ 13 + 16 × 8 = 17
On interchanging the mathematical signs, we get –
⇒ 39 ÷ 3 – 13 + 16 × 8 = 17
⇒ 13 – 13 + 16 × 8
⇒ 13 – 13 + 128
⇒ 128 ≠ 17
Fourth option: × and ÷
39 – 3 ÷ 13 + 16 × 8 = 17
On interchanging the mathematical signs, we get –
⇒ 39 – 3 × 13 + 16 ÷ 8 = 17
⇒ 39 – 3 × 13 + 2
⇒ 39 – 39 + 2
⇒ 2 ≠ 17
Here, only the first option satisfies the R.H.S. of the equation. Hence, the first option is correct.

Q3. Directions: If A means +, B means –, C means ÷, and D means ×, then 63 C 9 A 16 B 32 D 3 C 8 = ?

1. 11 (Correct)

2. 13

3. 10

4. 9

Solution:
Given:
63 C 9 A 16 B 32 D 3 C 8 = ?
On replacing the alphabet with the symbols, we get –
= 63 ÷ 9 + 16 – 32 × 3 ÷ 8
= 7 + 16 – 12
= 23 – 12
= 11
Hence, the first option is correct.

Q4.Directions: If × means +, ÷ means ×, − means ÷, and + means −, then what will be the value of the following expression?

32 × 6 + 10 − 4 ÷ 8 = ?

1. 18 (Correct)

2. 20

3. 22

4. 24

Solution:
Given:
32 × 6 + 10 – 4 ÷ 8 = ?

On interchanging the mathematical signs, we get –
= 32 + 6 – 10 ÷ 4 × 8
= 32 + 6 – 2.5 × 8
= 32 + 6 – 20
= 18

Hence, the first option is correct.

Q5. Directions: Which two signs should be interchanged to make the given equation correct?

12 + 156 ÷ 13 × 6 – 100 = 50

1. ÷ and ×

2. + and × (Correct)

3. – and ×

4. ÷ and –

Solution:
Given:
12 + 156 ÷ 13 × 6 – 100 = 50
Let's check the options –
First option: ÷ and ×
⇒ 12 + 156 × 13 ÷ 6 – 100 = 50
Solving the L.H.S. of the equation –
= 12 + 338 – 100
= 250 ≠ 50
Second option: + and ×
⇒ 12 × 156 ÷ 13 + 6 – 100 = 50
Solving the L.H.S. of the equation –
= 12 × 12 + 6 – 100
= 144 + 6 – 100
= 50
Third option: – and ×
⇒ 12 + 156 ÷ 13 – 6 × 100 = 50
Solving the L.H.S. of the equation –
= 12 + 12 – 6 × 100
= 12 + 12 – 600
= –576 ≠ 50
Fourth option: ÷ and –
⇒ 12 + 156 – 13 × 6 ÷ 100 = 50
Solving the L.H.S. of the equation –
= 12 + 156 – 13 × 0.06
= 12 + 156 – 0.78
= 167.22 ≠ 50
So, only the second option satisfies the given equation. Hence, the second option is correct.

Practice Questions for Interchanging Symbols and Numbers-Based Questions

Q1. Directions: Which two signs and two numbers (Not digits) should be interchanged in the given equation to make it correct?

9 ÷ 3 + 7 × 4 – 5 = 20

1. ÷ and –, 5 and 4

2. × and –, 3 and 5

3. + and ×, 9 and 7 (Correct)

4. ÷ and –, 7 and 5

Solution:

Given:
9 ÷ 3 + 7 × 4 – 5 = 20

Let's check the given options –
First Option: ÷ and –, 5 and 4
⇒ 9 – 3 + 7 × 5 ÷ 4 = 20
Solving the L.H.S. of the equation –
= 9 – 3 + 7 × 1.25
= 9 – 3 + 8.75
= 14.75 ≠ 20
Second option: × and –, 3 and 5
⇒ 9 ÷ 5 + 7 – 4 × 3 = 20
Solving the L.H.S. of the equation –
= 1.8 + 7 – 4 × 3
= 1.8 + 7 – 12
= –3.2 ≠ 20
Third option: + and ×, 9 and 7
⇒ 7 ÷ 3 × 9 + 4 – 5 = 20
Solving the L.H.S. of the equation –
= 21 + 4 – 5
= 20
Fourth option: ÷ and –, 7 and 5
⇒ 9 – 3 + 5 × 4 ÷ 7 = 20
Solving the L.H.S. of the equation –
= 9 – 3 + 5 × 0.57
= 9 – 3 + 2.85
= 8.85 ≠ 20

So, only the third option satisfies the given equation. Hence, the third option is correct.

Q2. Directions: By interchanging the given two signs and numbers, which of the following equations will be correct?

× and +, 9 and 6

1. 7 × 6 ÷ 3 + 9 – 8 = 17 (Correct)

2. 6 × 8 – 9 ÷ 3 + 5 = 50

3. 7 + 6 × 4 ÷ 9 – 8 = 8

4. 9 × 7 + 4 ÷ 1 – 6 = 7

Solution:
Let's check the options –
First option: 7 × 6 ÷ 3 + 9 – 8 = 17
On interchanging the given numbers and symbols, the equation becomes –
= 7 + 9 ÷ 3 × 6 – 8
= 7 + 18 – 8
= 17
Second option: 6 × 8 – 9 ÷ 3 + 5 = 50
On interchanging the given numbers and symbols, the equation becomes –
= 9 + 8 – 6 ÷ 3 × 5
= 9 + 8 – 10
= 17 – 10
= 7 ≠ 50
Third option: 7 + 6 × 4 ÷ 9 – 8 = 8
On interchanging the given numbers and symbols, the equation becomes –
= 7 × 9 + 4 ÷ 6 – 8
= 63 + 0.66 – 8
= 63.66 – 8
= 55.66 ≠ 8
Fourth option: 9 × 7 + 4 ÷ 1 – 6 = 7
On interchanging the given numbers and symbols, the equation becomes –
= 6 + 7 × 4 ÷ 1 – 9
= 6 + 7 × 4 – 9
= 6 + 28 – 9
= 25 ≠ 7
Hence, the first option is correct.

Q3. Directions: Which two signs and two numbers (Not digits) of the equation should be interchanged to make it correct?

13 × 12 ÷ 36 + 11 – 7 = 35

1. + and ×, 36 and 7

2. + and –, 12 and 7

3. × and ÷, 13 and 36

4. × and ÷,11 and 7 (Correct)

Solution:
Given:
13 × 12 ÷ 36 + 11 – 7 = 35
Let's check the given options –
First option: + and ×, 36 and 7
13 × 12 ÷ 36 + 11 – 7 = 35
On interchanging the mathematical signs and numbers, we get –
= 13 + 12 ÷ 7 × 11 – 36
= 13 + 1.71 × 11 – 36
= 13 + 18.81 – 36
= 31.81 – 36
= –4.19 ≠ 35
Second option: + and –, 12 and 7
13 × 12 ÷ 36 + 11 – 7 = 35
On interchanging the mathematical signs and numbers, we get –
= 13 × 7 ÷ 36 – 11 + 12
= 13 × 0.19 – 11 + 12
= 2.47 – 11 + 12
= 3.47 ≠ 35
Third option: × and ÷, 13 and 36
13 × 12 ÷ 36 + 11 – 7 = 35
On interchanging the mathematical signs and numbers, we get –
= 36 ÷ 12 × 13 + 11 – 7
= 3 × 13 + 11 – 7
= 39 + 11 – 7
= 50 – 7
= 43 ≠ 35
Fourth option: × and ÷,11 and 7
13 × 12 ÷ 36 + 11 – 7 = 35
On interchanging the mathematical signs and numbers, we get –
= 13 ÷ 12 × 36 + 7 – 11
= 39 + 7 – 11
= 46 – 11
= 35
So, the fourth option satisfies the R.H.S. of the equation. Hence, the fourth option is correct.

Q4. Directions: By interchanging the given two numbers (not digits) which of the following equations will not be correct?

4 and 6

1. 2 + 6 × 5 – 4 = 16

2. 4 + 5 – 6 = 7

3. 6 ÷ 2 – 4 × 5 = –28

4. 6 × 3 – 4 ÷ 1 = 3 (Correct)

Solution:
Let's check the options –
First option: 2 + 6 × 5 – 4 = 16
On interchanging the given numbers, the equation becomes –
⇒ 2 + 4 × 5 – 6 = 16
Solving the L.H.S. of the equation –
= 2 + 20 – 6
= 22 – 6
= 16
Second option: 4 + 5 – 6 = 7
On interchanging the given numbers, the equation becomes –
⇒ 6 + 5 – 4 = 7
Solving the L.H.S. of the equation –
= 11 – 4
= 7
Third option: 6 ÷ 2 – 4 × 5 = –28
On interchanging the given numbers, the equation becomes –
⇒ 4 ÷ 2 – 6 × 5 = –28
Solving the L.H.S. of the equation –
= 2 – 6 × 5
= 2 – 30
= –28
Fourth option: 6 × 3 – 4 ÷ 1 = 3
On interchanging the given numbers, the equation becomes –
⇒ 4 × 3 – 6 ÷ 1 = 3
Solving the L.H.S. of the equation –
= 4 × 3 – 6
= 12 – 6
= 6 ≠ 3
So, only the equation in the fourth option does not satisfy the R.H.S. of the given equation. Hence the fourth option is correct.

Q5. Directions: Which two numbers (not digits) should be interchanged to make the given equation correct?

5 – 6 ÷ 3 × 9 + 1 = 0

1. 1 and 0

2. 6 and 9

3. 5 and 9

4. 6 and 3

Solution:
Given:
5 – 6 ÷ 3 × 9 + 1 = 0
Let's check the options –
First option: 1 and 0
5 – 6 ÷ 3 × 9 + 1 = 0
On interchanging the numbers, we get –
⇒ 5 – 6 ÷ 3 × 9 + 0 = 1
⇒ 5 – 2 × 9 + 0 = 1
⇒ 5 – 18 + 0 = 1
⇒ –13 ≠ 1
Second option: 6 and 9
5 – 6 ÷ 3 × 9 + 1 = 0
On interchanging the numbers, we get –
⇒ 5 – 9 ÷ 3 × 6 + 1 = 0
⇒ 5 – 3 × 6 + 1 = 0
⇒ 5 – 18 + 1 = 0
⇒ –12 ≠ 0
Third option: 5 and 9
5 – 6 ÷ 3 × 9 + 1 = 0
On interchanging the numbers, we get –
⇒ 9 – 6 ÷ 3 × 5 + 1 = 0
⇒ 9 – 2 × 5 + 1 = 0
⇒ 9 – 10 + 1 = 0
⇒ 0
Fourth option: 6 and 3
5 – 6 ÷ 3 × 9 + 1 = 0
On interchanging the numbers, we get –
⇒ 5 – 3 ÷ 6 × 9 + 1 = 0
⇒ 5 – 0.5 × 9 + 1 = 0
⇒ 5 – 4.5 + 1 = 0
⇒ 1.5 ≠ 0
Here, only the third option satisfies the equation. Hence, the third option is correct.

Verbal Reasoning Topics

The candidates who are preparing for the upcoming entrance and Government exams can also refer to the links given below and master the reasoning ability section:

Practice Questions for Fill-in-the-Blanks-Based Questions

Q1. Directions: Select the correct combination of mathematical signs to sequentially replace the * signs and balance the given equation.

99 * 33 * 66 * 22 * 44 * 50

1. ÷, +, ×, +, =

2. +, −, ÷, −, =

3. ÷, +, ÷, +, =

4. ÷, −, +, ×, =

Solution:
Given:
99 * 33 * 66 * 22 * 44 * 50
Let's check the given options –
First Option: ÷, +, ×, +, =
⇒ 99 ÷ 33 + 66 × 22 + 44 = 50
Solving the L.H.S. of the equation –
= 3 + 66 × 22 + 44
= 3 + 1452 + 44
= 1499 ≠ 50
Second Option: +, −, ÷, −, =
⇒ 99 + 33 − 66 ÷ 22 − 44 = 50
Solving the L.H.S. of the equation –
= 99 + 33 − 3 − 44
= 132 − 3 − 44
= 85 ≠ 50
Third Option: ÷, +, ÷, +, =
⇒ 99 ÷ 33 + 66 ÷ 22 + 44 = 50
Solving the L.H.S. of the equation –
= 3 + 3 + 44
= 50
Fourth Option: ÷, −, +, ×, =
⇒ 99 ÷ 33 − 66 + 22 × 44 = 50
Solving the L.H.S. of the equation –
= 3 − 66 + 22 × 44
= 3 − 66 + 968
= 905 ≠ 50
So, only the third option satisfies the given equation. Hence, the third option is correct.

Q2. Directions: Select the correct combination of mathematical signs to sequentially replace the * signs and balance the given equation.
21 * 3 * 36 * 2 * 23 = 68

1. ÷, −, ×, +

2. ÷, ×, +, −

3. +, ×, −, ÷

4. ×, −, ÷, +

Solution:
Given:
21 * 3 * 36 * 2 * 23 = 68
Let's check the given options –
First option: ÷, −, ×, +
⇒ 21 ÷ 3 − 36 × 2 + 23 = 68
Solving the L.H.S. of the equation –
= 7 − 36 × 2 + 23
= 7 − 72 + 23
= −42 ≠ 68
Second option: ÷, ×, +, −
⇒ 21 ÷ 3 × 36 + 2 − 23 = 68
Solving the L.H.S. of the equation –
= 7 × 36 + 2 − 23
= 252 + 2 − 23
= 231 ≠ 68
Third option: +, ×, −, ÷
⇒ 21 + 3 × 36 − 2 ÷ 23 = 68
Solving the L.H.S. of the equation –
= 21 + 3 × 36 − 0.09
= 21 + 108 − 0.09
= 128.91 ≠ 68
Fourth option: ×, −, ÷, +
⇒ 21 × 3 − 36 ÷ 2 + 23 = 68
Solving the L.H.S. of the equation –
= 21 × 3 − 18 + 23
= 63 − 18 + 23
= 68
So, only the fourth option satisfies the given equation. Hence, the fourth option is correct.

Q3. Directions: Select the correct combination of mathematical signs to sequentially replace the * signs and balance the given equation.
268 * 4 * 8 * 5 * 14 = 41

1. +, ×, −, ÷

2. ×, ÷, +, −

3. ÷, ×, +, −

4. ÷, −, ×, +

Solution:
Given:
268 * 4 * 8 * 5 * 14 = 41
Let's check the options –
First option: +, ×, −, ÷
⇒ 268 + 4 × 8 − 5 ÷ 14 = 41
Solving the L.H.S. of the equation –
⇒ 268 + 4 × 8 − 0.36
⇒ 268 + 32 − 0.36
⇒ 299.64 ≠ 41
Second option: ×, ÷, +, −
⇒ 268 × 4 ÷ 8 + 5 − 14 = 41
Solving the L.H.S. of the equation –
⇒ 268 × 0.5 + 5 − 14
⇒ 134 + 5 − 14
⇒ 125 ≠ 41
Third option: ÷, ×, +, −
⇒ 268 ÷ 4 × 8 + 5 − 14 = 41
Solving the L.H.S. of the equation –
⇒ 67 × 8 + 5 − 14
⇒ 536 + 5 − 14
⇒ 527 ≠ 41
Fourth option: ÷, −, ×, +
⇒ 268 ÷ 4 − 8 × 5 + 14 = 41
Solving the L.H.S. of the equation –
⇒ 67 − 8 × 5 + 14
⇒ 67 − 40 + 14
⇒ 41
Here, only the fourth option satisfies the equation. Hence, the fourth option is correct.

Q4. Directions: Select the correct combination of mathematical signs to sequentially replace the * signs and to balance the given equation.
(130 * 4) * 21 * 485 * (28 * 2)

1. +, −, =, −, ×

2. ÷, +, =, −, ×

3. ×, −, =, −, ÷

4. ×, −, =, +, ÷

Solution:
Given:
(130 * 4) * 21 * 485 * (28 * 2)
Let's check the options −
First option: +, −, =, −, ×
⇒ (130 + 4) − 21 = 485 − (28 × 2)
L.H.S. = (130 + 4) − 21 = 134 − 21 = 113
R.H.S. = 485 − (28 × 2) = 485 − 56 = 429
L.H.S. ≠ R.H.S.
Second option: ÷, +, =, −, ×
⇒ (130 ÷ 4) + 21 = 485 − (28 × 2)
L.H.S. = (130 ÷ 4) + 21 = 32.5 + 21 = 53.5
R.H.S. = 485 − (28 × 2) = 485 − 56 = 429
L.H.S. ≠ R.H.S.
Third option: ×, −, =, −, ÷
⇒ (130 × 4) − 21 = 485 − (28 ÷ 2)
L.H.S. = (130 × 4) − 21 = 520 − 21 = 499
R.H.S. = 485 − (28 ÷ 2) = 485 − 14 = 471
L.H.S. ≠ R.H.S.
Fourth option: ×, −, =, +, ÷
⇒ (130 × 4) − 21 = 485 + (28 ÷ 2)
L.H.S. = (130 × 4) − 21 = 520 − 21 = 499
R.H.S. = 485 + (28 ÷ 2) = 485 + 14 = 499
L.H.S. = R.H.S.
Hence, the fourth option is correct.

Q5. Directions: Select the correct combination of mathematical signs to sequentially replace the * signs and balance the given equation.
54 * 6 * 72 * 8 * 3 * 15

1. ÷, +, ÷, −, =

2. ÷, −, −, +, =

3. +, ÷, ×, +, =

4. ×, −, −, +, =

Solution:
Given:
54 * 6 * 72 * 8 * 3 * 15
Let's check the given options –
First option: ÷, +, ÷, −, =
⇒ 54 ÷ 6 + 72 ÷ 8 – 3 = 15
Solving the L.H.S. of the equation –
= 9 + 9 – 3
= 18 – 3
= 15
Second option: ÷, –, –, +, =
⇒ 54 ÷ 6 – 72 – 8 + 3 = 15
Solving the L.H.S. of the equation –
= 9 – 72 – 8 + 3
= 12 – 72 – 8
= –68 ≠ 15
Third option: +, ÷, ×, +, =
⇒ 54 + 6 ÷ 72 × 8 + 3 = 15
Solving the L.H.S. of the equation –
= 54 + 0.67 + 3
= 57.67 ≠ 15
Fourth option: ×, –, –, +, =
⇒ 54 × 6 – 72 – 8 + 3 = 15
Solving the L.H.S. of the equation –
= 324 – 72 – 8 + 3
= 327 – 72 – 8
= 247 ≠ 15
So, only the first option satisfies the given equation. Hence, the first option is correct.

Mathematical Operations Questions for SSC/ RRB exams

Q-1. Directions: If A denotes addition, B denotes multiplication, C denotes subtraction, and D denotes division, then what will be the value of the following equation:
27 B 3 C (11 A 3) A 14 B (100 D 10) = ?
1) 207
2) 117
3) 221
4) 111

Solution:
27 B 3 C (11 A 3) A 14 B (100 D 10) = ?
After replacing the letters with the mathematical signs, we get:
= 27 × 3 – (11 + 3) + 14 × (100 ÷ 10)
= 27 × 3 – 14 + 14 × 10
= 81 – 14 + 140
= 207
So, 207 is the answer to the given equation. Hence, the first option is correct.

Q-2. Directions: Which two signs and two numbers should be interchanged in the following equation to make it correct:
19 × 12 - 51 ÷ 34 + 17 = 197
1) 17 and 51, × and –
2) 51 and 17, × and ÷
3) 34 and 51, × and +
4) 34 and 51, + and ÷

Solution:
Interchanging the numbers and signs according to the options, to balance the equation –
Let's check the options –
First option: 17 and 51, × and –
⇒19 – 12 × 17 ÷ 34 + 51 = 197
19 – 12 × 0.5 + 51 = 197
19 – 6 + 51 = 197
64 ≠ 197
Second option: 51 and 17, × and ÷
⇒19 ÷ 12 – 17 × 34 + 51 = 197
1.58 – 17 × 34 + 51 = 197
1.58 – 578 + 51 = 197
– 525.42 ≠ 197
Third option: 34 and 51, × and +
⇒19 + 12 – 34 ÷ 51 × 17 = 197
19 + 12 – 0.66 × 17 = 197
19 + 12 – 11.22 = 197
19.78 ≠ 197
Fourth option: 34 and 51,+ and ÷
⇒19 × 12 – 34 + 51 ÷ 17 = 197
19 × 12 – 34 + 3 = 197
228 – 34 + 3 = 197
197 = 197
So, the fourth option satisfies the given equation. Hence, the fourth option is correct.

Q-3. Directions: Select the correct combination of the mathematical signs to replace star symbols (*) in the below equation and thereby balance it.
65 * 5 * 17 * 24 * 21 * 224

1) ÷, ×, +, –, =

2) +, ×, –, ÷, =

3) ÷, ×, –, +, =

4) ×, +, –, ÷, =

Solution:

Replace * with the mathematical signs and solve the equations one by one using BODMAS.

First options: ÷, ×, +, –, =

65 ÷ 5 × 17 + 24 – 21 = 224

On solving the L.H.S. of the given equation –

= 65 ÷ 5 × 17 + 24 – 21

= 13 × 17 + 24 – 21

= 221 + 24 – 21

= 224

Second option: +, ×, –, ÷, =

65 + 5 × 17 – 24 ÷ 21 = 224

On solving the L.H.S. of the given equation –

= 65 + 5 × 17 – 24 ÷ 21

= 65 + 5 × 17 – 1.143

= 65 + 85 – 1.143

= 148.857 ≠ 224

Third option: ÷, ×, –, +, =

65 ÷ 5 × 17 – 24 + 21 = 224

On solving the L.H.S. of the given equation –

= 13 × 17 – 24 + 21

= 221 – 24 + 21

= 218 ≠ 224

Fourth option: ×, +, –, ÷, =

65 × 5 + 17 – 24 ÷ 21 = 224

On solving the L.H.S. of the given equation –

= 65 × 5 + 17 – 1.14

= 325 + 17 – 1.14

= 340.86 ≠ 224

So, the first option satisfies the equation. Hence, the first option is correct.

Mathematical Operations Questions for Bank Clerk/ Insurance Assistant exams

Q-1. Directions: If × means ÷, – means +, ÷ means × and + means –, then 84 × 7 ÷ 4 – 16 × 8 ÷ 2 + 14 = ?
1) 36

2) 38

3) 44

4) 24

Solution:

After interchanging the given mathematical signs, we get –

⇒ 84 ÷ 7 × 4 + 16 ÷ 8 × 2 – 14

⇒ 12 × 4 + 2 × 2 – 14

⇒ 48 + 4 – 14

⇒ 38

So, 38 is the answer to the given equation. Hence, the second option is correct.

Q-2. Directions: If 617 @ 342 = 572 and 483 @ 342 = 141, then 280 @ 82 = ?

1)632

2)891

3) 188

4) 721

Solution:

Equation I: 617 @ 342 = 572

617 – 342 = 275; On reversing the order of digits of 275, we get 572.

Equation II: 483 @ 342 = 141

483 – 342 = 141; On reversing the order of digits of 141 we get 141.

Similarly, for Equation III: 280 @ 82 = ?

280 – 82 = 198; On reversing the order of digits of 198, we get 891.

Hence, the second option is correct.

Common Mistakes in Solving Mathematical Operations Questions

Many students struggle with mathematical operations reasoning questions because they rush through the process or misinterpret symbols. In exams like SSC, CUET, VITEEE, and Banking, even a small mistake in following the rules or BODMAS order can lead to wrong answers. Below are the most common mistakes you should avoid while solving symbolic operations reasoning questions.

Ignoring the Given Instructions or Rules

One of the most frequent mistakes candidates make in mathematical operations reasoning questions is neglecting the exact instructions. In exams like CUET, SSC, and IPMAT, symbols are often redefined, and missing these small details can lead to completely wrong answers. Always read the directions carefully before attempting symbolic operations.

Confusing Between Symbols and Their Real Meanings

In symbolic operations reasoning questions, students often mix the newly assigned meaning of symbols (+, −, ×, ÷) with their actual values. For example, if “×” is defined as “+”, you must replace it accordingly. Confusing the symbols is one of the biggest errors seen in mathematical operations questions and answers PDF practice sets.

Rushing Without Verifying Each Step

Competitive exams are time-bound, and many candidates try to solve these reasoning questions too quickly. Skipping verification leads to silly mistakes. It’s important to cross-check each step, especially when solving mathematical operations reasoning questions SSC exams.

Overlooking the Order of Operations (BODMAS Rule)

Another common mistake is ignoring the BODMAS rule while solving symbolic problems. Even when symbols are replaced, the order of operations (Bracket, Of, Division, Multiplication, Addition, Subtraction) remains the same. Misapplying BODMAS leads to incorrect answers in reasoning questions for competitive exams.

Tricks and Shortcuts for Mathematical Operations Reasoning

Mathematical operations reasoning questions can be solved faster with simple shortcuts and logical approaches. These tricks help in identifying patterns, reducing errors, and saving time in exams. Below are some of the most effective methods.

Step-by-Step Approach to Solve Symbolic Operations Reasoning Questions

Break the question into smaller steps. Replace each symbol with its new meaning before performing calculations. Following a systematic method ensures accuracy while practicing mathematical operations reasoning questions PDF and mock tests.

Using Elimination Method for Tough Options

When faced with tricky symbolic operations reasoning questions, use the elimination method. Test each option by applying the given rules. This saves time and is particularly helpful in exams like SSC, Banking, CUET, and VITEEE.

Identifying Repeated Patterns in Mathematical Operations

Many mathematical operations reasoning questions follow recurring patterns such as swapped symbols or inverse operations. Identifying these patterns quickly can help in solving questions faster and scoring better in reasoning for all competitive exams.

How to Prepare for Mathematical Operations in Competitive Exams

Preparing for mathematical operations reasoning questions requires consistent practice, strong command over symbolic operations, and smart exam strategies. These questions are commonly asked in CUET, VITEEE, MAH MBA CET, IPMAT, SSC, Banking, and other competitive exams. Below are some effective preparation tips.

Mathematical Operations in CUET, VITEEE, MAH MBA CET, and IPMAT

These exams often include mathematical operations and reasoning questions to test analytical ability. Focus on speed and accuracy by practising symbolic reasoning and pattern-based problems from past papers and PDFs.

Solving Mathematical Operations Reasoning Questions SSC & Banking Exams

In SSC and Banking exams, mathematical operations reasoning questions SSC are designed to check logical interpretation. Practicing previous year questions and mathematical operations questions and answers helps candidates build confidence and reduce errors.

Using Online Quizzes and PDFs for Regular Practice

Free and paid resources like mathematical operations reasoning questions PDF, quizzes, and sectional tests are available online. Regular practice through these platforms helps in mastering shortcuts, avoiding common mistakes, and preparing efficiently for competitive exams like SSC, Banking, CUET, and IPMAT.

Non-Verbal Reasoning Topics

Non-verbal reasoning questions test your ability to analyze patterns, shapes, and figures without using language-based logic. These types of questions are very common in competitive exams like SSC, CUET, Banking, and Railways, making them important for quick problem-solving practice. Below are the key non-verbal reasoning topics you should focus on.

About the Faculty
Tanu Gupta, with over a decade of experience as a reasoning faculty, specializes in preparing students for various entrance examinations and career development. Her extensive work with multiple educational platforms and institutions has honed her expertise in logical and analytical thinking. Her dedication to innovative teaching methods ensures these articles provide practical insights and expert guidance.