Exam Prep
JEE Main 2021 Analysis: Coordinate Geometry Made Easy, Important Questions And Solutions

Synopsis
Coordinate Geometry is an important part of JEE Main, the tough entrance exam for engineering admission to premier colleges. In JEE Main 2021 some 840 questions were from Mathematics and Coordinate Geometry accounted for 11.07 percent of them. Read through this article for a comprehensive analysis of Coordinate Geometry and know about the most important topics from where maximum questions were asked.

Synopsis
Coordinate Geometry is an important part of JEE Main, the tough entrance exam for engineering admission to premier colleges. In JEE Main 2021 some 840 questions were from Mathematics and Coordinate Geometry accounted for 11.07 percent of them. Read through this article for a comprehensive analysis of Coordinate Geometry and know about the most important topics from where maximum questions were asked.
The National Testing Agency (NTA) has been conducting the Joint Entrance Examination (JEE) Main, Paper 1 for admission to undergraduate engineering programs (B.E/B.Tech.) at NITs, IIITs, and other premiere Institutes. Paper 1 is also an eligibility test for JEE Advanced, which is conducted for admission to IITs. Paper 2 is conducted for admission into B.Arch and B.Plan courses across the country.
The JEE Main syllabus consists of three subjects, that is, Physics, Chemistry, and Mathematics, and the Mathematics syllabus contains 16 chapters. JEE Main is a highly competitive exam and so aspirants should have a good command of each topic in every subject to score well in the exam. Mathematics has one-third weightage and therefore it becomes crucial to have a good hold on important topics in Mathematics syllabus. For a dedicated candidate, it is essential to have a winning plan that contains prioritizing important topics and analysis of the previous years’ papers to understand the breadth and depth of the topics.
This article analyzes Coordinate Geometry, one of the important Mathematics chapters of JEE Main 2021. It includes topics like Rectangular Cartesian Coordinate System, Distance Formula, Section Formula, Locus, Straight Lines, Circles, Conic Section, Parabola, Ellipse, Hyperbola, and some other topics as well. This article explains concepts with the help of previous years’ questions.
A total of 28 papers were held in both shifts in all the four sessions of JEE Main 2021. In these papers, 840 questions were from mathematics. Out of them 93 questions, that is, 11.07%, were from Coordinate Geometry. It shows how important this chapter is for JEE Main aspirants. The concepts, number of questions asked and weightage is given in the following table.
Concepts And Number Of Questions
Topic | Number Of Questions | Weightage (%) |
Circle | 35 | 37.63 |
Parabola | 17 | 18.27 |
Ellipse | 12 | 12.90 |
Hyperbola | 8 | 8.60 |
Line | 42 | 45.16 |
Tangent | 32 | 34.40 |
Normal | 9 | 9.67 |
Locus | 14 | 15.05 |
Area Of Triangle | 11 | 11.82 |
It can be observed that out of 93 questions, concepts of a Line, Circle, Tangent are used in 42, 35 and 32 questions respectively. Concepts of the Circle contain standard and general forms of the equation of a circle, the equation of a circle when the endpoint of diameter is given, the intersection of circle and line, etc. Concepts of the line include an intersection of lines, the angle between two lines, condition for the intersection of three lines, coordinate of centroid, circumcenter, the orthocenter of a triangle, family of lines.
Solution of the following few questions from JEE Main 2021 show that command over multiple concepts is required to solve a problem. Practising every concept is essential as it can be difficult for students who are not aware or do not have a good hold on all the concepts to solve such questions.
Q.1 JEE Main 2021
The locus of a point, which moves such that the sum of squares of its distances from the points (0, 0), (1, 0), (0, 1), (1, 1) is 18 units, is a circle of diameter d. Then d2 is equal to
Solution
Let the point be P (h,k)
As per the question
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence,
![]()
Concepts Used
Distance formula, Concepts of locus, Equation of a circle.
Q.2 JEE Main 2021
Consider the parabola with vertex ![]() and the directrix
and the directrix ![]() . Let
. Let ![]() be the point where the parabola meets the line
be the point where the parabola meets the line ![]() . If the normal to the parabola at
. If the normal to the parabola at ![]() intersects the parabola again at the point
intersects the parabola again at the point ![]() , then
, then ![]() is equal to.
is equal to.
Solution
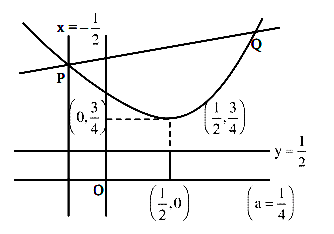
![]()
Equation of parabola
![]()
![]()
For point P
![]()
For PQ
![]()
![]()
![]()
Equation of PQ:
![]()
![]()
For point Q
![]()
![]()
![]()
![]()
Concepts Used
Intersection of line and parabola, Equation of a parabola, Concepts of the normal, Equation of a line in slope-intercept form, Distance formula.
Q.3 JEE Main 2021
The locus of mid-points of the line segments joining ![]() and the points on the ellipse
and the points on the ellipse ![]() are:
are:
Solution
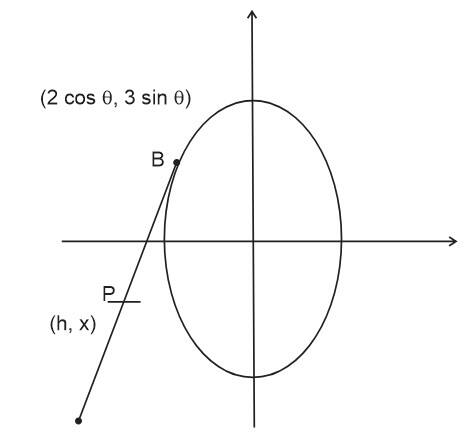
Let us take any parametric point ![]() on the ellipse
on the ellipse
Let ![]() be the midpoint of
be the midpoint of ![]()
So ![]()
![]()
Square and add;
![]()
Replace ![]()
![]()
![]()
![]()
Concepts Used
Point on the ellipse in parametric form, Concepts of locus.
Q.4 JEE Main 2021
The locus of the midpoints of the chords of the hyperbola ![]() which touch the parabola
which touch the parabola ![]() is:
is:
Solution
Let the midpoint of chord be P(h,k)
![]() equation of chord: T = S1
equation of chord: T = S1
![]()
![]()
![]()
![]()
Any tangent to ![]()
![]()
Comparing it with (i)
![]()
![]()
![]()
![]()
![]()
![]()
Concepts Used
Equation of cord, Tangent on a parabola, Concepts of locus
Q.5 JEE Main 2021
The point ![]() lies on the hyperbola
lies on the hyperbola ![]() having eccentricity
having eccentricity ![]() If the tangent and normal at P to the hyperbola intersects its conjugate axis at the points Q and R respectively, then QR is equal to
If the tangent and normal at P to the hyperbola intersects its conjugate axis at the points Q and R respectively, then QR is equal to
Solution
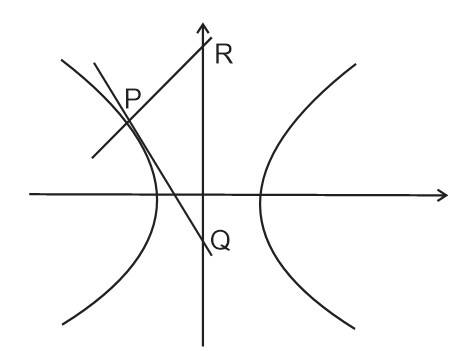
![]()
and ![]() lies on it, so
lies on it, so
![]()
![]()
![]()
Equation of the tangent at P:
T = 0
![]()
![]()
![]()
Normal at p
![]()
![]()
![]()
![]()
Concepts Used
Equation of hyperbola, a point on hyperbola, tangent and normal on hyperbola, distance formula.
An analysis of the previous year's question shows that Coordinate Geometry questions can be solved very easily by having command over the basic concepts of each topic. Practising as many questions as possible, doing calculations fast without making any errors and practising NCERT book problems are also important. Lastly, solving problems from previous years’ JEE Main exam is highly beneficial to ace the JEE Main exam as it will let you know beforehand what sort of questions to expect and that can give you an edge over other competitors.
Subscribe to Membership Plan
*Unlock all premium content and benefits:
Rate this Story
Latest Stories
JEE Advanced Cutoff 2024 - IIT JEE Cut off, Qualifying Marks

JEE Advanced Cut off 2023 - Know the qualifying cutoff marks to be considered for IIT admissions. Also, check the closing JEE Advanced 2023 cutoff ranks at which admissions closed in the IITs in the past years.
By
10 min read ⋆ 25 Apr'24
JEE Main Toppers 2023 - Know names of the 100 percentile scorers
57 min read ⋆ 25 Apr'24
Know the JEE Main 2023 cutoffs for NITs, IIITs and GFTIS
9 min read ⋆ 25 Apr'24
List of Medical Colleges Under 600 Rank in NEET UG
7 min read ⋆ 25 Apr'24
Careers360 helping shape your Career for a better tomorrow
250M+
Students
30,000+
Colleges
500+
Exams
1500+
E-Books
