Electron Configuration - Meaning, Definition, Rules, Table, FAQs

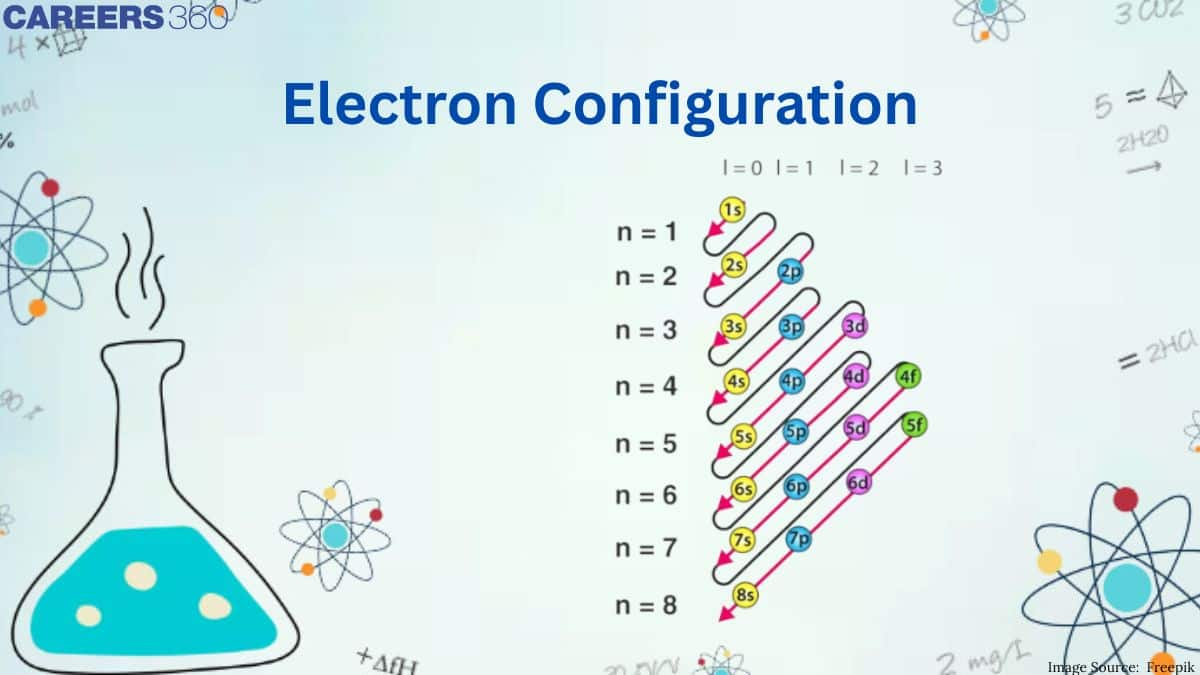
Electronic Configuration

Electronic configuration is the systematic arrangement of electrons of an atom in different energy levels (shells), subshells, and atomic orbitals around the nucleus. It describes how electrons are distributed in an atom according to increasing energy and specific filling rules.

Electronic configuration helps in understanding the chemical properties, valency, bonding nature, stability, and periodic behavior of elements.

Rules for Writing Electronic Configuration

The electronic configuration of an atom refers to the systematic arrangement of electrons in various energy levels and orbitals around the nucleus. Writing electronic configurations helps us understand the chemical behavior, valency, bonding nature, and periodic trends of elements.

Electrons are distributed in shells and subshells based on increasing energy. Each shell is designated by a principal quantum number (n = 1, 2, 3, …) and contains subshells such as s, p, d, and f. While writing electron configurations, electrons are filled in orbitals in such a way that the total energy of the atom remains minimum.

For example:

• Electronic configuration of Hydrogen (Z = 1) $\rightarrow 1 \mathrm{~s}^1$

• Electronic configuration of Oxygen (Z = 8) $\rightarrow 1 \mathrm{~s}^2 2 \mathrm{~s}^2 2 \mathrm{p}^4$

Rules for filling orbitals in Electron Configuration

1. Aufbau Rule: The term "Aufbeen" comes from the German word "aufbauen," which means "to build up." According to the Aufbau principle, electrons will first occupy lower-energy orbitals before moving on to higher-energy orbitals. The sum of the primary and azimuthal quantum numbers is used to compute the energy of an orbital. Electrons are filled in the following order according to this principle: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p.

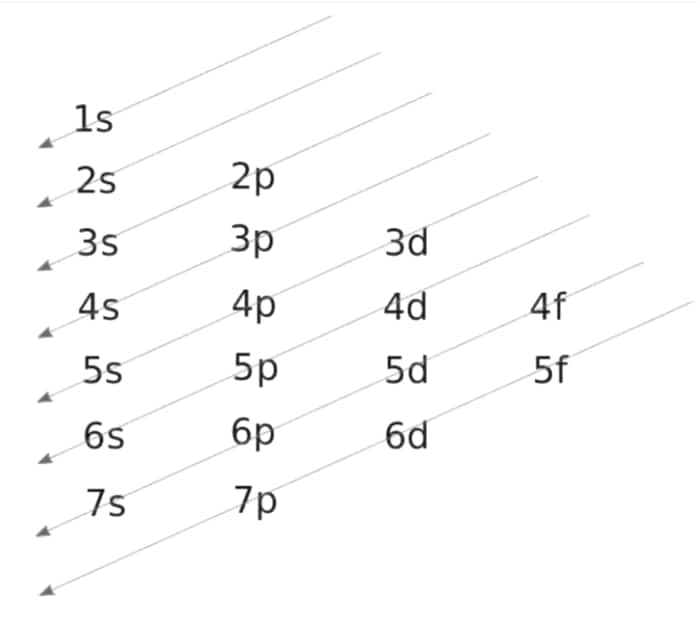
It's worth noting that the Aufbau principle has many exceptions, such as chromium and copper. The stability afforded by half-full or entirely filled subshell electronic configurations can occasionally explain these exceptions.

2. Pauli exclusion principle: According to the Pauli exclusion principle, an orbital can only hold a maximum of two electrons with opposite spins. “No two electrons in the same atom have the same values for all four quantum numbers,” says this principle. As a result, if two electrons have the same primary, azimuthal, and magnetic numbers, they must have opposite spins.

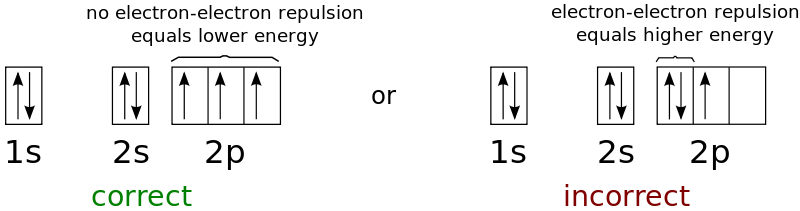
3. Hund’s Rule: This rule specifies the order in which electrons are filled in all of a subshell's orbitals. It asserts that before a second electron is inserted in an orbital, every orbital in a particular subshell is single-occupied by electrons. The electrons in orbitals with only one electron have the same spin in order to maximise the total spin (or the same values of the spin quantum number).

Example: the electronic configuration is $1 s^2 2 s^2 2 p^3$, it can be represented using hund’s rule as:

Related Topics link

• Periodic Table Elements
• 118 elements, their symbols and their atomic numbers
• Rutherfords Model of Atoms and Its Limitations
• Reactivity series
• First 20 Elements

Representation of Electronic Configuration of an Atom

Electronic configuration can be represented in different ways depending on the requirement:

1. Orbital Notation

In this method, each orbital is represented by a box and electrons by arrows $(\uparrow \downarrow)$, showing their spins.
Example for Nitrogen (Z = 7): $1 s^2 2 s^2 2 p^3$
Here, the three 2p electrons occupy separate orbitals with parallel spins.

2. Shell-wise Representation

Electrons are distributed among shells as K, L, M, N.
Example:

• Sodium $(Z=11) \rightarrow 2,8,1$

3. Noble Gas Configuration

To simplify writing, the configuration of the nearest noble gas is used as a core.
Example:

• Chlorine $(Z=17) \rightarrow[N e] 3 s^2 3 p^5$

This method is especially useful for writing configurations of transition and inner-transition elements.

Related Topics link

• Electronic Configuration of First 30 Elements
• Electron Gain Enthalpy
• Homologous Series
• Atomic radius in periodic table in basic chemistry
• Classification of Elements in Modern Periodic Table

Noble Gas Electron Configuration

Also check-

Some Solved Examples

Question 1: Which of the following is electronic configration of Li ?
1) (correct) $1 \mathrm{~s}^2 2 \mathrm{~s}^1$

2) $1 s^2 2 s^2$

3) $1 s^1 2 s^1$

4) $1 \mathrm{~s}^1$

Solution:

As we have learnt-

Atomic number of Li is three.

Li : 1s²2s¹

Hence, the answer is the option (1).

Question 2: The electronic configuration of Einsteinium is: (Given atomic number of Einsteinium $=99$ )
1) $[\mathrm{Rn}] 5 \mathrm{f}^{12} 6 \mathrm{~d}^0 7 \mathrm{~s}^2$

2) (correct) $[\mathrm{Rn}] 5 \mathrm{f}^{11} 6 \mathrm{~d}^0 7 \mathrm{~s}^2$

3) $[\mathrm{Rn}] 5 \mathrm{f}^{13} 6 \mathrm{~d}^0 7 \mathrm{~s}^2$

4) $[\mathrm{Rn}] 5 \mathrm{f}^{10} 6 \mathrm{~d}^0 7 \mathrm{~s}^2$

Solution:

Einsteinium (atomic $\mathrm{No}=99$ ) : $[R n] 5 \mathrm{f}^{11} 6 \mathrm{~d}^0 7 \mathrm{~s}^2$

Hence, the answer is the option (2)

Question 3: The total number of species from the following in which one unpaired electron is present, is $\_\_\_\_$ .

$\mathrm{N}_2, \mathrm{O}_2, \mathrm{C}_2^{-}, \mathrm{O}_2^{-}, \mathrm{O}_2^{2-}, \mathrm{H}_2^{+}, \mathrm{CN}^{-}, \mathrm{He}_2^{+}$

Solution:

One unpaired $\mathrm{e}^{-}$is present in : $\mathrm{C}_2^{-} ; \mathrm{O}_2^{-} ; \mathrm{H}_2^{+} ; \mathrm{He}_2^{+}$

Hence, the answer is (4).

Question 4: The electronic configuration of an element is $1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^5 4 s^1$ This represents its:
1) Excited state
2) (correct) Ground state
3) Cationic form
4) Anionic form

Solution:

Ground state, because half-filled d - orbital is more stable.

Hence, the answer is the option (2).

Practice more question with link given below