Electrochemistry

Chemistry
Electrochemistry

Electrochemistry

Shivani PooniaUpdated on 30 Sep 2025, 12:35 PM IST

Have you ever thought about how a simple chemical reaction can produce an electric current? How does a battery light up your phone, and why can metals like zinc and copper generate electricity when placed in a solution? This is all possible because of electrochemistry. Electrochemistry is the interrelationship between chemical energy and electrical energy. It primarily studies converting electrical energy into chemical energy and vice versa through redox reactions.

This Story also Contains

Important Topics of Electrochemistry
Important Concepts and Laws
Preparation Tips for Electrochemistry
Prescribed Books

Electrochemistry

Electrochemistry is everywhere around us, from electric vehicles to electroplating. Some of the fundamental topics, like the electrolytic and Galvanic Cells, where chemical reactions are driven by electric currents, are discussed in this chapter. The Nernst Equation is one of the important concepts discussed in this chapter, which explains the relationship between temperature, potential of the cell, concentration of reactants, and products. The electrode potential explains how electrons move between the cathode and the anode.

The lithium-ion battery used in electric vehicles stores and discharges energy based on electrochemical reactions. Hydrogen-powered buses generate electricity by the conversion of Hydrogen and Oxygen into water. Electrochemistry is widely used in industrial processes like electroplating, which is used to protect material from corrosion, and rust is carried out through electrochemical processes.

Important Topics of Electrochemistry

Electrochemistry

Electrochemistry is the branch of chemistry that deals with the relationship between electrical energy and chemical reactions. It focuses on the study of redox reactions, where the transfer of electrons generates or requires electrical energy, forming the basis of batteries, electrolysis, and fuel cells.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download EBook

Galvanic Cells

Galvanic cells (or voltaic cells) are devices that convert chemical energy into electrical energy. Galvanic cells consist of two electrodes in separate half-cells connected by a conductive solution and a salt bridge, with electrons flowing from the anode to the cathode.

Salt Bridge

A salt bridge is a device used in galvanic cells to maintain electrical neutrality by allowing the flow of ions between the two half-cells. Salt bridge prevents charge buildup and sustains the cell's operation.

EMF of a Cell

The electromotive force (emf) of a cell is the potential difference between its two electrodes when no current flows. Emf of a cell is a measure of the cell's ability to drive electrons through an external circuit and is calculated using electrode potentials.

$E_{\text {cell }}=E_{\text {cathode }}-E_{\text {anode }}$
Where $E_{\text {cathode }}$ and $E_{\text {anode }}$ are the standard electrode potentials.

Example:
Daniell Cell: $\mathrm{Zn}\left|\mathrm{Zn}^{2+} \| \mathrm{Cu}^{2+}\right| \mathrm{Cu}$
$E_{\text {cell }}=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}-E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}=1.10 \mathrm{~V}$

Standard Hydrogen Electrode (SHE)

The Standard Hydrogen Electrode is a reference electrode with a defined potential of 0 V. It consists of a platinum electrode in contact with H₂ gas and it is used to determine standard electrode potentials of other half-cells.

Electrochemical Series

The electrochemical series ranks elements based on their standard electrode potentials. It helps predict the feasibility of redox reactions, with elements higher in the series acting as better oxidizing agents and those lower as reducing agents.

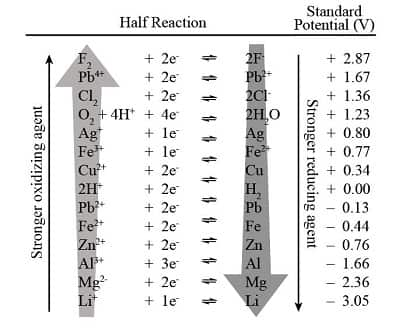
Standard electrode potential

Standard electrode potential measures the half-cell's tendency to gain or lose electrons when connected to the hydrogen electrode under standard conditions.

Standard electrode potential is expressed in Volts. It is represented by $E^{\circ}$.

Tendency to gain electrons is represented by positive $E^{\circ}$
Tendency to lose electrons is represented by $E^{\circ}$.

The potential of the Standard Hydrogen electrode is 0.00V.

Nernst Equation

The Nernst equation provides for the cell potential to its standard potential, temperature, and reactant/product concentrations. Nernst equation is crucial for understanding how EMF changes with varying conditions.

The Nernst equation is represented by:

$E=E^{\circ}-\frac{R T}{n F} \ln Q$

Concentration Cell

A concentration cell is a type of galvanic cell where the electrodes are identical but are in solutions of different concentrations. The concentration cell generates EMF due to the concentration gradient, driving ions to equalize the concentrations.

Specific Conductivity

Specific conductivity is the measure of a solution's ability to conduct electric current per unit length. Specific conductivity is expressed in Siemens per meter. It is represented by $\kappa$

The formula of Specific conductivity is:

$\kappa=\frac{1}{R} \times \frac{l}{A}$

Molar Conductivity

It is defined as the ability of an electrolytic solution to conduct electricity when one mole of electrolyte is dissolved and placed between electrodes that are 1 cm apart. Molar conductivity is represented by $\Lambda_m$ and is expressed in $\mathrm{S} \cdot \mathrm{cm}^2 \cdot \mathrm{~mol}^{-1}$.

The formula to calculate molar conductivity is:

$\Lambda_m=\frac{\kappa \times 1000}{C}$

Molar Conductivity for Strong Electrolytes:

Strong electrolytes like $\mathrm{NaCl}, \mathrm{HCl}, \mathrm{KNO}_3$ dissociate completely in solution, which produces a high concentration of ions.

Molar Conductivity for Weak Electrolytes:

Weak electrolytes like $\mathrm{NH}_4 \mathrm{OH}$ dissociates partially in solution producing fewer ions.

Kohlrausch's Law

Kohlrausch’s law states that the limiting molar conductivity of an electrolyte is the sum of the individual contributions of its ions. It is useful in determining dissociation constants and ion conductivities.

Faraday’s Laws of Electrolysis

Faraday gave two laws of Electrolysis

Faraday’s first law
Faraday's second law

Faraday's first law:

It states that the mass of substance deposited at the electrode during electrolysis is directly proportional to the electric charge passed through the electrolyte.

It is given by the formula:

$m=Z \times Q$

Second law of electrolysis:

The mass of substance deposited on different electrolytes when the same quantity of electric charge is passed through them is directly proportional to their chemical equivalents.

It is given by the formula:

$\frac{m_1}{m_2}=\frac{E_1}{E_2}$

Gibbs Free Energy of Reaction

The Gibbs free energy change (ΔG) for an electrochemical reaction is related to the cell emf by the equation ΔG=−nFE, where n is the number of electrons and F is Faraday's constant. Negative ΔG indicates a spontaneous reaction.

Types of Batteries - Primary and Secondary Cells

Primary cells, like dry cells, are non-rechargeable and provide energy until the reactants are exhausted. Secondary cells, like lead-acid and lithium-ion batteries, are rechargeable, allowing reversible chemical reactions to restore their charge.

Important Concepts and Laws

ELECTROCHEMISTRY
Electrochemistry is the branch of science that deals with the transformation of chemical energy into electrical energy and vice versa or it deals with the relationship between electrical and chemical energy produced in a redox reaction.

Galvanic Cell (or Voltanic Cell)
Consider the following redox reaction:

$\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \longrightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}(\mathrm{aq})$

In the above reaction, Zn displaces copper ions (Cu²⁺) from aqueous solution. This reaction can be achieved very easily in practice. Put a Zn rod into a solution of CuSO₄ (containing Cu²⁺ ions). It is observed that the blue color of the CuSO₄ solution disappears after some time. In this situation, Zn loses 2 electrons per atom, and Cu²⁺ ions in the solution accept them. Cu²⁺ ions from the solution in this manner are deposited in the form of solid Cu and Zn goes into the solution as Zn²⁺ (colorless). The reaction can well be understood in terms of two half-reactions:

Oxidation: & $\mathrm{Zn}(\mathrm{s}) \longrightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-}$
Reduction: & $\mathrm{Cu}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \longrightarrow \mathrm{Cu}(\mathrm{s})$

Now, we can make the same reaction take place even if the copper ions and zinc rod are not in direct contact. If we put the Cu²⁺ ions and Zn rod in two separate containers and connect the two by a conducting metallic wire and introduce an inverted U shape instrument (called as salt-bridge), then electrons will still be transferred through the connecting wires. The electrons from the Zn rod travel to Cu²⁺ ions through the connecting wires and the same reaction takes place. This flow of electrons through the wire generates electricity.

Galvanic Cell

The function of a Salt Bridge

A salt bridge acts as an electrical contact between the two half-cells.
It prevents the mechanical flow of the solution but it provides a free path for the migration of ions to maintain an electric current through the electrolyte solution. It prevents the accumulation of excess charges.
A salt bridge helps maintain the charge balance in the two half-cells.
A salt bridge minimizes/eliminates the liquid junction potential.
Liquid Junction Potential: The unequal rates of migration of the cations and anions across a liquid-liquid junction give rise to a potential difference across the junction. This potential difference across the liquid-liquid junction is called liquid junction
potential.

Preparation Tips for Electrochemistry

This chapter is one of the most important in Physical chemistry.
For preparing this chapter, there is no need for any pre-requisite chapter. Thus, prepare it freshly and actively.
All these basic concepts and rules of EMF of a cell, flow of current, redox reaction, mechanism of galvanic cell, and electrochemical cell, etc. must be understood well. Thus, prepare this chapter carefully. Try to solve numerical problems from the NCERT, as many such questions are asked in the examination.
In a nutshell, it can be said that although this chapter is not very long, it is a very simple and straightforward one. So always say a "Big YES" to this chapter.

Prescribed Books

For this chapter, first, the NCERT book is best for initial level preparation as well as for board exams. Now, after this, if you want to prepare for competitive exams like JEE and NEET, then these are the best books for you - O.P Tandon. Meanwhile, in preparation, you must continuously give mock tests to assess the depth of knowledge. Our platform will help you with the variety of questions for deeper knowledge with the help of videos, articles, and mock tests.

Previous Year Questions of Electrochemistry

Question 1: Consider the following half-cell reaction

$\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+6 \mathrm{e}^{-}+14 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+7 \mathrm{H}_2 \mathrm{O}(\mathrm{l})$

The reaction was conducted with the ratio of $\frac{\left[\mathrm{Cr}^{3+}\right]^2}{\left[\mathrm{Cr}_2 \mathrm{O}_7^{2-}\right]}=10^{-6}$. The pH value at which the EMF of the half cell will become zero is _______ . (nearest integer value)
[Given : standard half-cell reduction potential

$\left.\mathrm{E}_{\mathrm{C}_2 \mathrm{O}_{-}^2+\mathrm{H}^* / \mathrm{Cr}^{3+}}^{\mathrm{o}}=1.33 \mathrm{~V}, \frac{2.303 \mathrm{RT}}{\mathrm{~F}}=0.059 \mathrm{~V}\right]$

Answer:

$\mathrm{Cr}_2 \mathrm{O}_7^{2-}(\mathrm{aq})+6 \mathrm{e}^{-}+14 \mathrm{H}^{+}(\mathrm{aq}) \rightarrow 2 \mathrm{Cr}^{3+}(\mathrm{aq})+7 \mathrm{H}_2 \mathrm{O}(\mathrm{l})$

Using the Nernst equation

$\mathrm{E}_{\mathrm{Cr}_2 \mathrm{O}_7^{2-} / \mathrm{H}^{+} / \mathrm{Cr}^{3+}}=\mathrm{E}_{\mathrm{Cr}_2 \mathrm{O}_7^{2-} / \mathrm{H}^{+} / \mathrm{cr}^{3+}}^0-\frac{2.303 \mathrm{RT}}{6 \mathrm{~F}} \log \frac{\left[\mathrm{Cr}^{3+}\right]^2}{\left[\mathrm{Cr}_2 \mathrm{O}_7^{2-}\right]\left[\mathrm{H}^{+}\right]^{14}} $

$0=\mathrm{E}_{\mathrm{Cr}_2 \mathrm{O}_7^{2-} \mathrm{H}^{+} / \mathrm{C}^{3+}}^0-\frac{0.059}{6} \log \left(10^{-6}\left[\mathrm{H}^{+}\right]^{-14}\right)$

$0=1.33-\frac{0.059}{6}(-6+14 \cdot \mathrm{pH})$
$1.33=\frac{0.059}{6}(14 \cdot \mathrm{pH}-6)$

$1.33=0.00983(14 \cdot \mathrm{pH}-6)$
$\frac{1.33}{0.00983}=14 \cdot \mathrm{pH}-6 \Rightarrow 135.3 \approx 14 \cdot \mathrm{pH}-6$
$141.3=14 \cdot \mathrm{pH} \Rightarrow \mathrm{pH}=\frac{141.3}{14} = 10.1$
Hence, the answer is 10.

Q.2 The molar conductance of an infinitely dilute solution of ammonium chloride was found to be $185 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$ and the ionic conductance of hydroxyl and chloride ions are 170 and $70 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^1$, respectively. If the molar conductance of a 0.02 M solution of ammonium hydroxide is $85.5 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$, its degree of dissociation is given by $\mathrm{x} \times 10^{-1}$. The value of $x$ is _______ (Nearest integer).

Answer:

$\begin{aligned}
& \lambda_{\mathrm{m}}^{\prime \prime} \text { of } \mathrm{NH}_4 \mathrm{Cl}=185 \\
& \left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4}+\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{Cl}^{-}}=185 \\
& \left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4}=185-70=115 \mathrm{Scm}^2 \mathrm{~mol}^{-1} \\
& \left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4 \mathrm{OH}}=\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4^{\circ}}+\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{OH}^{-}} \\
& =115+170 \\
& \left(\lambda_{\mathrm{m}}^0\right)_{\mathrm{NH}_4 \mathrm{OH}}=285 \mathrm{Scm}^2 \mathrm{~mol}^{-1} \\
& \text { degree of dissociation }=\frac{\left(\lambda_{\mathrm{m}}\right)_{\mathrm{NH}_4 \mathrm{OH}}}{\left(\lambda_{\mathrm{m}}^{\circ}\right)_{\mathrm{NH}_4 \mathrm{OH}}} \\
& =\frac{85.5}{285} \\
& =0.3 \\
& =3 \times 10^{-1}
\end{aligned}$

Hence, the answer is 3.

Question 3: Give reason:

In the experimental determination of electrolytic conductance, Direct Current (DC) is not used.

Answer:

Direct Current (DC) is not used in the experimental determination of electrolytic conductance because it causes electrolysis and polarization at the electrodes.

Explanation:
1. Electrolysis occurs with DC:
Because DC causes continuous movement of ions in one direction, this leads to chemical changes at the electrodes, i.e., electrolysis, which interferes with accurate conductance measurement.
2. Polarization of electrodes:

Ions accumulate at the electrodes, forming concentration gradients or even gas bubbles (like $\mathrm{H}_2$ or $\mathrm{O}_2$).
This creates an extra resistance called electrode polarization, which distorts the actual conductance reading.

3. AC prevents these issues:

Alternating Current (AC) changes direction rapidly, so ions oscillate rather than accumulate.
This prevents electrolysis and minimizes polarization, allowing accurate and stable measurement of conductance.

DC is avoided because it causes electrolysis and electrode polarization, which interfere with the correct determination of electrolytic conductance. AC is used instead for accurate results.

Question 4: Calculate $\Lambda^{\circ} \mathrm{m}$ for acetic acid and its degree of dissociation ( $\alpha$ ) if its molar conductivity is $48.1 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$.
Given that

$\begin{aligned}
& \Lambda^{\circ} \mathrm{m}(\mathrm{HCl})=426 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\
& \Lambda^{\circ} \mathrm{m}(\mathrm{NaCl})=126 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1} \\
& \Lambda^{\circ} \mathrm{m}\left(\mathrm{CH}_3 \mathrm{COONa}\right)=91 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1}
\end{aligned}$

Solution:

For calculating the $\Lambda_m^{\circ}$

Given:

By applying Kohlrausch's Law calculate $\Lambda_m^{\circ}\left(\mathrm{CH}_3 \mathrm{COOH}\right)$

$\Lambda_m^{\circ}(\text { weak electrolyte })=\Lambda_m^{\circ}(\text { strong acid })+\Lambda_m^{\circ}(\text { salt })-\Lambda_m^{\circ}(\text { common ion salt })$
So,

$\begin{gathered}
\Lambda_m^{\circ}\left(\mathrm{CH}_3 \mathrm{COOH}\right)=\Lambda_m^{\circ}(\mathrm{HCl})+\Lambda_m^{\circ}\left(\mathrm{CH}_3 \mathrm{COONa}\right)-\Lambda_m^{\circ}(\mathrm{NaCl}) \\
=426+91-126=391 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1}
\end{gathered}$
For Calculating degree of dissociation $\alpha=\frac{\Lambda_m}{\Lambda_m^{\circ}}$
We have
Molar conductivity at concentration $c: \Lambda_m=48.1 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$
Limiting molar conductivity: $\Lambda_m^{\circ}=391 \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$

$\alpha=\frac{\Lambda_m}{\Lambda_m^{\circ}}=\frac{48.1}{391} \approx 0.123 \text { or } 12.3 \%$

Hence, the answer is 0.123 and 391$ \Omega^{-1} \mathrm{~cm}^2 \mathrm{~mol}^{-1}$

Practice More Questions From The Link Given Below

For more questions to practice, the following MCQs will help in the preparation for competitive examinations

Faraday’s Laws of Electrolysis-Practice MCQs	Gibbs Free Energy of Reaction-Practice MCQs
Concentration Cells-Practice MCQs	Molar Conductivity-Practice MCQs
Kohlrausch's Law-Practice MCQs	Nernst Equation-Practice MCQs

News and Notifications

Assam government to stop hiring teachers in colleges with low student enrolment

Careers360 Faculty Research Award 2023: Researchers across 27 disciplines to get awards

UGC Chairman, Australian minister discuss regulations on foreign university campuses in India

RTE Act: HC asks Centre to reply to plea on common syllabus, curriculum for children in India

Warm, helpful, funny - Rajnish was an ideal colleague

Latest updates

Cambridge IGCSE Exam Date 2025: June & November Session (Zone 4)

Oct 04, 2025

Cambridge Time Table 2025-26: IGCSE, O Level, International A Level and Pre-U level Exam Dates

Oct 04, 2025

Vidya Lakshmi Education Loan: Schemes, Eligibility & Repayment Details

Oct 04, 2025

IB Admit Card 2025 – Download IB Examination Admit Card Here

Oct 03, 2025

IB 2025 Exam Schedule: All exam zones (A, B, C)

Oct 03, 2025

View all

Student Community: Where Questions Find Answers

Ask and get expert answers on exams, counselling, admissions, careers, and study options.

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Applications Open

NEET Test Series

NCERT notes Class 11 Maths	NCERT solutions for class 11 Physics.	NCERT exemplar solutions for class 11 Physics.
NCERT notes Class 11 Physics	NCERT solutions for class 11 Chemistry.	NCERT exemplar solutions for class 11 Chemistry.
NCERT notes Class 11 Chemistry	NCERT solutions for class 11 Mathematics.	NCERT exemplar solutions for class 11 Mathematics.
NCERT notes Class 11 Biology	NCERT solutions for class 11 Biology.	NCERT exemplar solutions for class 11 Biology.

Electrochemistry

Important Topics of Electrochemistry

Electrochemistry

Galvanic Cells

Salt Bridge

EMF of a Cell

Standard Hydrogen Electrode (SHE)

Electrochemical Series

Nernst Equation

Concentration Cell

Molar Conductivity

Kohlrausch's Law

Faraday’s Laws of Electrolysis

Gibbs Free Energy of Reaction

Types of Batteries - Primary and Secondary Cells

Important Concepts and Laws

NEET

JEE Main Paper 1

JEE Advanced

JEE Main Paper 2

BITSAT B.E

BITSAT M.Sc.

BITSAT B.Pharma

NEET AYUSH All India Counseling

Maharashtra MBBS/BDS Counselling

Arunachal Pradesh MBBS/BDS Admissions

NEET AYUSH All India Counseling

Government Ayurvedic Medical College, Bengaluru

Government Ayurveda Medical College and Hospital, Mysore